Lý thuyết Tỉ số và tỉ số phần trăm Toán 6 Chân trời sáng tạo — Không quảng cáo

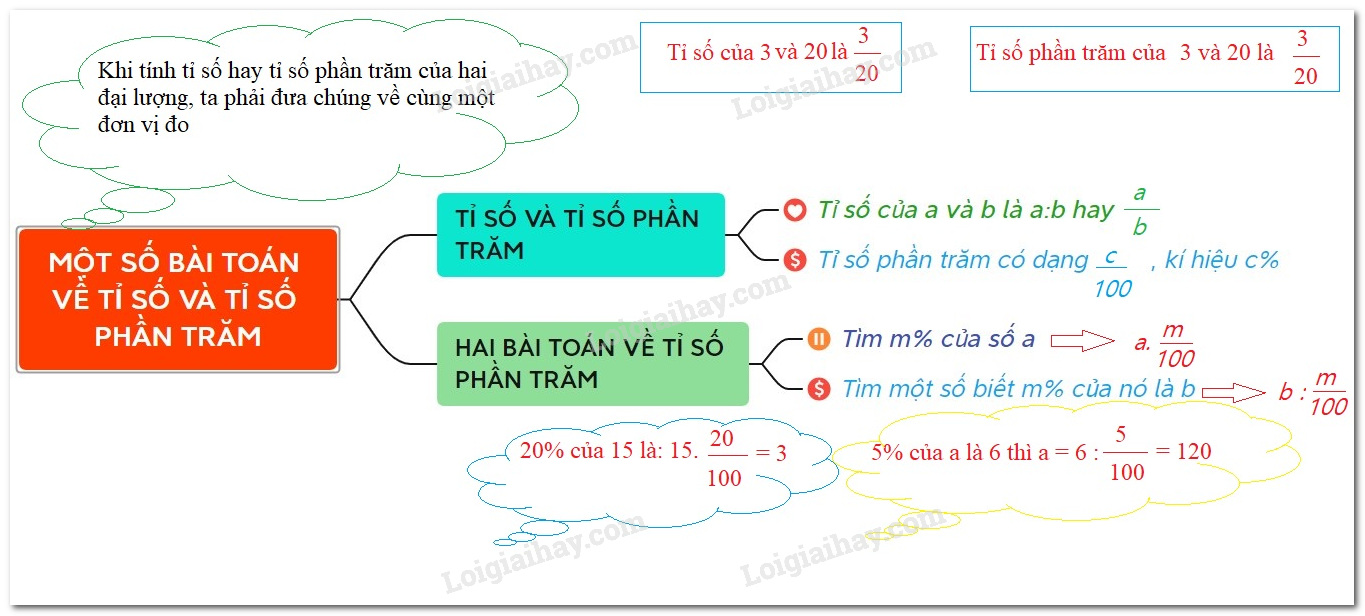
I. Tỉ số

a) Tỉ số của hai số

Chú ý : Nếu tỉ số của $ a$  và $ b$  được viết dưới dạng $ \dfrac{a}{b}$  thì ta cũng gọi $ a$  là tử số và $ b$  là mẫu số.

Ví dụ:

Tỉ số của $  - 5$  và $ 7$  là: $ \dfrac{{ - 5}}{7}$ .

b) Tỉ số của hai đại lượng

Nhận xét:

Tỉ số của hai đại lượng thể hiện độ lớn của đại lượng này so với đại lượng kia.

Chú ý:

- Phân số $ \dfrac{a}{b}$  thì cả $ a$  và $ b$  phải là các số nguyên.

- Tỉ số $ \dfrac{a}{b}$  thì $ a$  và $ b$  có thể là các số nguyên, phân số, hỗn số, số thập phân,…

Ví dụ:

Tỉ số chiều dài hai đoạn thẳng $ AB = 1,5\,\,\,cm$  và $ CD = \dfrac{1}{3}\,cm$  là: $ 1,5:\dfrac{1}{3}$ .

II. Tỉ số phần trăm

Ví dụ:

a) Tỉ số phần trăm của $ 3$ và $ 6$ là:

$ \dfrac{{3.100}}{6}\% = \dfrac{{300}}{6}\% = 50\% .$

b) Tỉ số phần trăm của $ - 2,3$ và $ 10$  là: $ \dfrac{{ - 2,3.100}}{{10}}\% = - 23\% $

Chú ý: Tỉ số $ \dfrac{{a.100}}{b}$  không nhất thiết là số nguyên.

III. Tính tỉ số của hai số

Để tính tỉ số của hai số ta tính $ a:b$  hoặc $ \dfrac{a}{b}$  $ \left( {b \ne 0} \right)$

IV. Tính tỉ số phần trăm của hai đại lượng

Để tính tỉ số phần trăm của a và b, ta làm như sau:

Bước 1 . Viết tỉ số $ \dfrac{a}{b}$

Bước 2 . Tính số $ \dfrac{{a.100}}{b}$  và viết thêm % vào bên phải số vừa nhận được.

V. Viết các số thập phân, phân số dưới dạng tỉ số phần trăm và ngược lại

- Viết một số a dưới dạng dùng kí hiệu %: \(a = \dfrac{{a.100}}{{100}} = (100.a)\% \)

- Viết \(a\% \) dưới dạng phân số: \(a\%  = \dfrac{a}{{100}}\)

- Đổi số thập phân ra phân số: \(\overline {a,bc}  = \dfrac{{\overline {abc} }}{{100}} = \overline {abc} \% ;\,\,\,\,\,\overline {a,{b_1}{b_2}...{b_n}}  = \dfrac{{a{b_1}{b_2}...{b_n}}}{{{{10}^n}}}\)

- Một phân số tối giản có mẫu số chỉ có ước số nguyên tố là 2 hoặc 5 thì có thể viết dưới dạng số thập phân (hữu hạn).