Lý thuyết Tính chất cơ bản của phân số
Tải vềLý thuyết Tính chất cơ bản của phân số Toán 6 Chân tời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
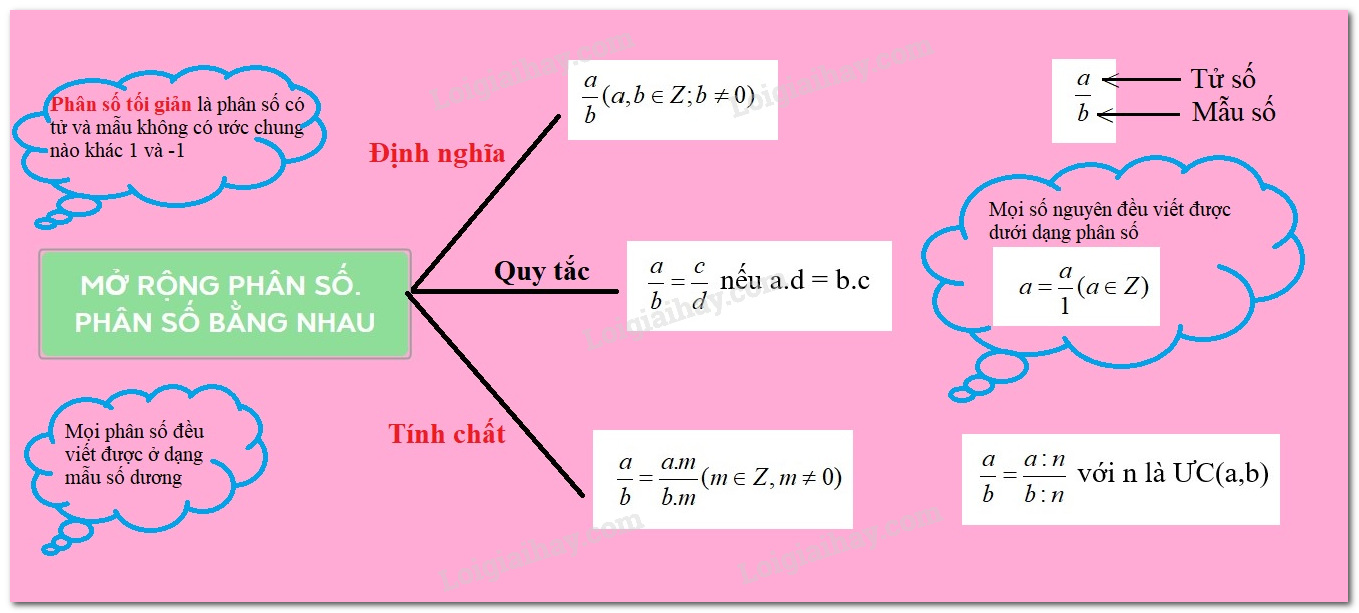
I. Tính chất 1: Nhân cả tử và mẫu của một phân số với một số khác 0
Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho.
$\dfrac{a}{b} = \dfrac{{a.m}}{{b.m}}$ với $m \in Z$ và $m \ne 0$ .
Ví dụ:
a) $\dfrac{2}{3} = \dfrac{{2.4}}{{3.4}} = \dfrac{8}{{12}}$
b) $\dfrac{{ - 5}}{7} = \dfrac{{ - 5.2}}{{7.2}} = \dfrac{{ - 10}}{{14}}$
II. Tính chất 2: Chia cả tử và mẫu của một phân số với một ước chung
Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng ta được một phân số mới bằng phân số đã cho.
$\dfrac{a}{b} = \dfrac{{a:n}}{{b:n}}$ với $n \in $ƯC$\left( {a;b} \right)$.
Ví dụ:
a) $\dfrac{9}{{15}} = \dfrac{{9:3}}{{15:3}} = \dfrac{3}{5}$
b) $\dfrac{{ - 14}}{{ - 21}} = \dfrac{{ - 14:7}}{{ - 21:7}} = \dfrac{2}{3}$
III. Quy đồng mẫu nhiều phân số
Bước 1: Viết các phân số đã cho về phân số có mẫu dương. Tìm BCNN của các mẫu dương đó để làm mẫu chung
Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu)
Bước 3: Nhân tử và mẫu của mỗi phân số ở Bước 1 với thừa số phụ tương ứng.
Ví dụ :
Để quy đồng mẫu hai phân số $\dfrac{1}{6}$ và $\dfrac{3}{{ - 8}}$, ta làm như sau:
- Đưa về phân số có mẫu dương: $\dfrac{1}{6}$ và $\dfrac{{ - 3}}{8}$
- Tìm mẫu chung: $BC(6;\,8) = 24$
- Tìm thừa số phụ: $24:6 = 4;\,24:8 = 3$
- Ta có: $\dfrac{1}{6} = \dfrac{{1.4}}{{6.4}} = \dfrac{4}{{24}}$ và $\dfrac{3}{{ - 8}} = \dfrac{{ - 3}}{8} = \dfrac{{ - 3.3}}{{8.3}} = \dfrac{{ - 9}}{{24}}$.
IV. Rút gọn phân số
a) Khái niệm phân số tối giản:
Phân số tối giản là phân số mà tử và mẫu chỉ có ước chung là $1$ và $ - 1$
b) Cách rút gọn phân số
Bước 1: Tìm ƯCLN của tử và mẫu khi đã bỏ dấu “-” (nếu có)
Bước 2: Chia cả tử và mẫu cho ƯCLN vừa tìm được, ta có phân số tối giản.
Ví dụ:
Để rút gọn phân số $\dfrac{{ - 15}}{{24}}$ ta làm như sau:
- Tìm ƯCLN của mẫu: ƯCLN(15; 24)=3.
- Chia cả tử và mẫu cho ƯCLN: $\dfrac{{ - 15}}{{24}} = \dfrac{{ - 15:3}}{{24:3}} = \dfrac{{ - 5}}{8}$.
Ta được $\dfrac{{ - 5}}{8}$ là phân số tối giản.
CÁC DẠNG TOÁN VỀ TÍNH CHẤT CƠ BẢN CỦA PHÂN SỐ
I. Xác định các phân số bằng nhau
Áp dụng tính chất cơ bản của phân số
$\dfrac{a}{b} = \dfrac{{a.m}}{{b.m}}$ với $m \in Z$ và $m \ne 0$ ; $\dfrac{a}{b} = \dfrac{{a:n}}{{b:n}}$ với $n \in $ ƯC $\left( {a;b} \right)$ .
II. Tìm số chưa biết của đẳng thức hai phân số
Áp dụng tính chất cơ bản của phân số để biến đổi hai phân số đã cho thành hai phân số bằng chúng nhưng có từ (hoặc mẫu) như nhau. Khi đó mẫu (hoặc tử) của chúng phải bằng nhau. Từ đó tìm được số chưa biết. Hoặc áp dụng định nghĩa hai phân số bằng nhau.
III. Rút gọn phân số. Rút gọn biểu thức dạng phân số
- Chia cả tử và mẫu của phân số $\dfrac{a}{b}$ cho ƯCLN của $a$ và $b$ để rút gọn thành phân số tối giản ( bỏ dấu “-” nếu có)
- Trường hợp biểu thức có dạng phân số, ta cần làm xuất hiện các thừa số chung của tử và mẫu rồi rút gọn các thừa số chung đó.
IV. Tìm các phân số tối giản trong các phân số cho trước
Để tìm phân số tối giản trong các phân số cho trước, ta tìm ƯCLN của tử và mẫu đối với từng phân số. Phân số nào có ƯCLN này là $1$ thì đó là phân số tối giản.
Ví dụ:
Phân số $\dfrac{{ - 5}}{7}$ tối giản vì ƯCLN $\left( {5,7} \right) = 1.$
V. Viết dạng tổng quát của tất cả các phân số bằng một phân số cho trước
Ta thực hiện hai bước:
- Rút gọn phân số đã cho đến tối giản, chằng hạn ta được phân số tối giản $\dfrac{m}{n}$ ;
- Dạng tổng quát của các phân số phải tìm là $\dfrac{{m.k}}{{n.k}}$ ( $k$ $ \in $ $\mathbb{Z}$ , $k$ $ \ne 0).$