Ôn tập toàn bộ lý thuyết về Phân số - Các phép tính với phân số môn Ôn hè Toán lớp 4 — Không quảng cáo

1. Phân số

Mỗi phân số có tử số và mẫu số. Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác 0 viết dưới gạch ngang.

Ví dụ:

\(\frac{4}{7}\) ;  $\frac{1}{5}$ ;  $\frac{{14}}{{13}}$ là những phân số.

2. Cách đọc, viết phân số

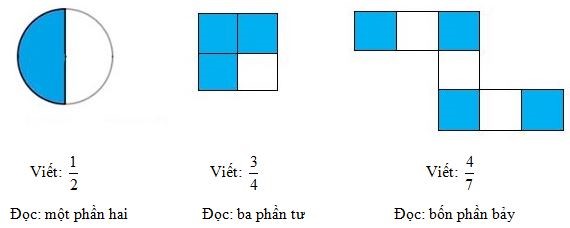
3. Phân số và phép chia số tự nhiên

Thương của phép chia số tự nhiên cho số tự nhiên (khác 0) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia.

Ví dụ:

$3:4 = \frac{3}{4}$     ;           $9:7 = \frac{9}{7}$

4. Phân số lớn hơn 1, bằng 1, nhỏ hơn 1

- Phân số có tử số lớn hơn mẫu số là phân số lớn hơn 1.

Ví dụ: $\frac{7}{6} > 1$        ;           $\frac{{11}}{7} > 1$

- Phân số có tử số bé hơn mẫu số là phân số lớn hơn 1.

Ví dụ: $\frac{7}{9} < 1$        ;           $\frac{{12}}{{13}} < 1$

- Phân số có tử số bằng mẫu số là phân số bằng 1.

Ví dụ: $\frac{8}{8} = 1$

5. Rút gọn phân số

Khi rút gọn phân số có thể làm như sau:

- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn \(1\).

- Chia tử số và mẫu số cho số đó.

- Cứ làm như thế cho đến khi nhận được phân số tối giản.

Ví dụ: $\frac{9}{{12}} = \frac{{9:3}}{{12:3}} = \frac{3}{4}$

$\frac{{18}}{{27}} = \frac{{18:9}}{{27:9}} = \frac{2}{3}$

6. Phép cộng hai phân số

Muốn cộng hai phân số cùng mẫu số, ta cộng hai tử số với nhau và giữ nguyên mẫu số.

$\frac{a}{c} + \frac{b}{c} = \frac{{a + b}}{c}$

Ví dụ: $\frac{3}{7} + \frac{2}{7} = \frac{5}{7}$

Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.

Ví dụ: $\frac{2}{3} + \frac{4}{5} = \frac{{10}}{{15}} + \frac{{12}}{{15}} = \frac{{22}}{{15}}$

7. Phép trừ hai phân số

Muốn trừ hai phân số cùng mẫu số, ta trừ tử số của phân số thứ nhất cho tử số của phân số thứ hai và giữ nguyên mẫu số.

$\frac{a}{c} - \frac{b}{c} = \frac{{a - b}}{c}$

Ví dụ: $\frac{7}{9} - \frac{2}{9} = \frac{5}{9}$

Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi trừ hai phân số đó.

Ví dụ $\frac{5}{8} - \frac{1}{3} = \frac{{15}}{{24}} - \frac{8}{{24}} = \frac{7}{{24}}$

8. Phép nhân phân số

$\frac{a}{b} \times \frac{c}{d} = \frac{{a \times c}}{{b \times d}}$

Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.

Ví dụ: $\frac{5}{{12}} \times \frac{3}{{10}} = \frac{{5 \times 3}}{{12 \times 10}} = \frac{{15}}{{120}} = \frac{1}{8}$

Hoặc $\frac{5}{{12}} \times \frac{3}{{10}} = \frac{{5 \times 3}}{{12 \times 10}} = \frac{{\not 5 \times \not 3}}{{4 \times \not 3 \times \not 5 \times 2}} = \frac{1}{8}$

9. Phép chia phân số

Quy tắc: Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.

$\frac{a}{b}:\frac{c}{d} = \frac{a}{b} \times \frac{d}{c} = \frac{{a \times d}}{{b \times c}}$

Ví dụ: $\frac{7}{{15}}:\frac{2}{3} = \frac{7}{{15}} \times \frac{3}{2} = \frac{{21}}{{30}} = \frac{7}{{10}}$