Trả lời phần câu hỏi ôn tập chương 4: Hàm số y=ax^2-Phương trình bậc hai một ẩn trang 60, 61 SGK toán 9 tập 2
Trả lời phần câu hỏi ôn tập chương 4: Hàm số y=ax^2-Phương trình bậc hai một ẩn trang 60, 61 SGK toán 9 tập 2. Hãy vẽ đồ thị của các hàm số y = 2x2, y = -2x2. Dựa vào đồ thị để trả lời các câu hỏi sau:...
Câu hỏi 1
Hãy vẽ đồ thị của các hàm số \(y = 2x^2, y = -2x^2.\) Dựa vào đồ thị để trả lời các câu hỏi sau:
a) Nếu a > 0 thì hàm số \(y = ax^2\) đồng biến khi nào? Nghịch biến khi nào?
Với giá trị nào của x thì hàm số đạt giá trị nhỏ nhất? Có giá trị nào của x để hàm số đạt giá trị lớn nhất không?
Nếu a < 0 thì hàm số đồng biến khi nào? Nghịch biến khi nào? Với giá trị nào của x thì hàm số đạt giá trị lớn nhất? Có giá trị nào của x để hàm số đạt giá trị nhỏ nhất không?
b) Đồ thị của hàm số \(y = ax^2\) có những đặc điểm gì (trường hợp a > 0 , trường hợp a < 0)
Phương pháp giải:
Dựa vào tính chất và đặc điểm của đồ thị hàm số \(y=ax^2\)
Lời giải chi tiết:
Vẽ đồ thị:
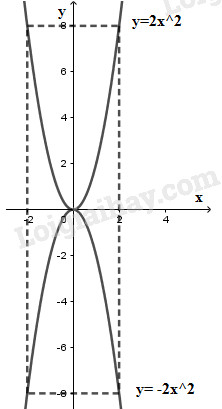
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị nào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số \(y = ax^2\) là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.
Câu hỏi 2
Đối với phương trình bậc hai \(ax^2 + bx + c = 0 (a ≠ 0),\) hãy viết công thức tính \(Δ, Δ'.\)
Khi nào thì phương trình vô nghiệm?
Khi nào phương trình có hai nghiệm phân biệt? Viết công thức nghiệm.
Khi nào phương trình có nghiệm kép? Viết công thức nghiệm.
Vì sao khi a và c trái dấu thì phương trình có hai nghiệm phân biệt?
Phương pháp giải:
Dựa vào kiến thức về công thức nghiệm và công thức nghiệm thu gọn
Lời giải chi tiết:
* Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\,\,(a \ne 0)\)
và biệt thức \(\Delta = {b^2} - 4ac\), \(\Delta' = {b'^2} - ac\) với \(b'=\dfrac{b}{2}\)
TH1. Nếu \(\Delta < 0\) (hoặc \(\Delta' < 0)\) thì phương trình vô nghiệm.
TH2. Nếu \(\Delta = 0\) (hoặc \(\Delta' =0)\) thì phương trình có nghiệm kép: \({x_1} = {x_2} = - \dfrac{b}{2a}\) (hoặc \({x_1} = {x_2} = - \dfrac{b'}{a}\) )
TH3. Nếu \(\Delta > 0\) (hoặc \(\Delta' >0)\) thì phương trình có hai nghiệm phân biệt: \({x_{1,2}} = \dfrac{{ - b \pm \sqrt \Delta }}{{2a}}\) (hoặc \({x_{1,2}} = \dfrac{{ - b' \pm \sqrt \Delta ' }}{{a}}\))
* Khi a và c trái dấu thì \(a.c<0\) nên \(\Delta = {b^2} - 4ac>0\), do đó phương trình \(a{x^2} + bx + c = 0\,\,(a \ne 0)\) có hai nghiệm phân biệt.
Câu hỏi 3
Viết hệ thức Vi-et đối với các nghiệm của phương trình bậc hai \(ax^2 + bx + c = 0 (a ≠ 0),\)
Nêu điều kiện để phương trình \(ax^2 + bx + c = 0 (a ≠ 0),\) có một nghiệm bằng 1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình \(1954x^2 + 21x – 1975 = 0\)
Nêu điều kiện để phương trình \(ax^2 + bx + c = 0 (a ≠ 0),\) có một nghiệm bằng -1. Khi đó, viết công thức nghiệm thứ hai. Áp dụng: nhẩm nghiệm của phương trình \(2005x^2 + 104x – 1901 = 0\)
Phương pháp giải:
Áp dụng kiến thức về hệ thức Vi-et và ứng dụng tại đây.
Lời giải chi tiết:
+ Hệ thức Vi-ét:
Nếu \({x_1},{\rm{ }}{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0\,(a \ne 0)\) thì:
\(\left\{\begin{matrix} x_{1} + x_{2} = -\dfrac{b}{a}& & \\ x_{1}x_{2}=\dfrac{c}{a} & & \end{matrix}\right.\)
+) Nếu phương trình \(a{x^2} + bx + c = 0\,(a \ne 0)\) có \(a + b + c = 0\) thì phương trình có một nghiệm \({x_1}= 1\), còn nghiệm kia là \({x_2}=\dfrac{c}{a}.\)
Áp dụng: Phương trình \(1954x^2 + 21x – 1975 = 0\) có \(a=1954, b=21, c=-1975\) nên \(a+b+c=1954+21+(-1975)=0\), do đó phương trình có một nghiệm \({x_1}= 1\), còn nghiệm kia là \({x_2}=\dfrac{-1975}{1954}.\)
+) Nếu phương trình \(a{x^2} + bx + c = 0\,(a \ne 0)\) có \(a - b + c = 0\) thì phương trình có nghiệm là \({x_1}= -1\), còn nghiệm kia là \({x_2}=\dfrac{-c}{a}\).
Áp dụng: Phương trình \(2005x^2 + 104x – 1901 = 0\) có \(a=2005, b=104, c=-1901\) nên \(a-b+c=2005-104+(-1901)=0\), do đó phương trình có một nghiệm \({x_1}= -1\), còn nghiệm kia là \({x_2}=\dfrac{1901}{2005}.\)
Câu hỏi 4
Nêu cách tìm hai số, biết tổng S và tích P của chúng.
Tìm hai số u và v trong mỗi trường hợp sau:
\(\begin{array}{l} a)\left\{ \begin{array}{l} u + v = 3\\ uv = - 8 \end{array} \right.\\ b)\left\{ \begin{array}{l} u + v = 5\\ uv = 10 \end{array} \right. \end{array}\)
Phương pháp giải:
Tìm hai số khi biết tổng và tích của chúng
Nếu hai số có tổng bằng \(S\) và tích bằng \(P\) và \({S^2}-{\rm{ }}4P{\rm{ }} \ge {\rm{ }}0\) thì hai số đó là hai nghiệm của phương trình: \({x^2}-{\rm{ }}Sx{\rm{ }} + {\rm{ }}P{\rm{ }} = {\rm{ }}0\).
Lời giải chi tiết:
+) Tìm hai số khi biết tổng và tích của chúng
Nếu hai số có tổng bằng \(S\) và tích bằng \(P\) và \({S^2}-{\rm{ }}4P{\rm{ }} \ge {\rm{ }}0\) thì hai số đó là hai nghiệm của phương trình: \({x^2}-{\rm{ }}Sx{\rm{ }} + {\rm{ }}P{\rm{ }} = {\rm{ }}0\).
a) Đặt \(u+v=S,u.v=P\) ta có
\(\left\{ \begin{array}{l} S = 3\\ P = - 8 \end{array} \right.\)
Ta có: \(S^2-4P=41>0\)
Khi đó \(u,v\) là hai nghiệm của phương trình \(x^2-3x-8=0\)
Ta có: \(\Delta = {\left( { - 3} \right)^2} - 4.1.\left( { - 8} \right) = 41 > 0\)
Nên phương trình có hai nghiệm phân biệt:
\({x_1} = \dfrac{{3 + \sqrt {41} }}{2};{x_2} = \dfrac{{3 - \sqrt {41} }}{2}\)
Vậy \(u = \dfrac{{3 + \sqrt {41} }}{2};v = \dfrac{{3 - \sqrt {41} }}{2}\)
Hoặc \(u = \dfrac{{3 - \sqrt {41} }}{2};v = \dfrac{{3 + \sqrt {41} }}{2}\)
b)
Đặt \(u+v=S,u.v=P\) ta có
\(\left\{ \begin{array}{l} S = -5\\ P = 10 \end{array} \right.\)
Ta có: \(S^2-4P=25-40=-15<0\) nên không có hai số \(u,v\) thỏa mãn đề bài.
Câu hỏi 5
Nêu cách giải phương trình trùng phương \(ax^4 + bx^2 + c = 0,(a ≠ 0)\)
Phương pháp giải:
Đặt ẩn phụ \(t = x^2\) (1) (điều kiện \(t ≥ 0).\)
Từ đó đưa về phương trình bậc hai ẩn t đã biết cách giải.
Lời giải chi tiết:
Xét phương trình \(ax^4 + bx^2 + c = 0,(a ≠ 0)\)
Đặt ẩn phụ \(t = x^2\) (1) (điều kiện \(t ≥ 0).\)
Khi đó phương trình đã cho tương đương với một phương trình bậc 2 ẩn t là:
\(at^2 + bt + c = 0\) (2)
- Giải phương trình (2) để tìm t, so sánh với điều kiện.
- Thay giá trị t thỏa mãn vào (1) để tìm x.