Trắc nghiệm Bài 3: Phép trừ và phép chia Toán 6 Chân trời sáng tạo
Đề bài
Phép tính \(x - 5\) thực hiện được khi
-
A.
\(x < 5\)
-
B.
\(x \ge 5\)
-
C.
\(x < 4\)
-
D.
\(x = 3\)
Cho phép tính \(231 - 87\). Chọn câu đúng.
-
A.
\(231\) là số trừ
-
B.
\(87\) là số bị trừ
-
C.
\(231\) là số bị trừ
-
D.
\(87\) là hiệu
Cho phép tính \(x:3 = 6\), khi đó thương của phép chia là
-
A.
\(x\)
-
B.
\(6\)
-
C.
\(3\)
-
D.
\(18\)
Tính 1 454-997
-
A.
575
-
B.
567
-
C.
457
-
D.
754
Trong phép chia có dư \(a\) chia cho \(b,\) trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\) duy nhất sao cho:
\(a = b.q + r\)
Khẳng định nào sau đây đúng ?
-
A.
\(r \ge b\)
-
B.
\(0 < b < r\)
-
C.
\(0 < r < b\)
-
D.
\(0 \le r < b\)
Biểu diễn phép chia \(445:13\) dưới dạng \(a = b.q + r\) trong đó \(0 \le r < b\)
-
A.
\(445 = 13.34 + 3\)
-
B.
\(445 = 13.3 + 34\)
-
C.
\(445 = 34.3 + 13\)
-
D.
\(445 = 13.34\)
-
A.
1
-
B.
2
-
C.
3
-
D.
4
-
A.
Phép cộng của 1 và 2
-
B.
Phép trừ của 3 và 2
-
C.
Phép cộng của 1 và 3
-
D.
Phép trừ của 3 và 1
Dạng tổng quát của số tự nhiên chia hết cho \(3\) là:
-
A.
\(3k\,\left( {k \in N} \right)\)
-
B.
\(5k + 3\,\left( {k \in N} \right)\)
-
C.
\(3k + 1\,\left( {k \in N} \right)\)
-
D.
\(3k + 2\,\left( {k \in N} \right)\)
Dạng tổng quát của số tự nhiên chia cho \(5\) dư \(2\) là
-
A.
\(2k + 5\,\left( {k \in N} \right)\)
-
B.
\(5k + 2\,\left( {k \in N} \right)\)
-
C.
\(2k\,\left( {k \in N} \right)\)
-
D.
\(5k + 4\,\left( {k \in N} \right)\)
Tình nhanh \(49.15 - 49.5\) ta được kết quả là
-
A.
\(490\)
-
B.
\(49\)
-
C.
\(59\)
-
D.
\(4900\)
Kết quả của phép tính $12.100 + 100.36 - 100.19$ là
-
A.
\(29000\)
-
B.
\(3800\)
-
C.
\(290\)
-
D.
\(2900\)
Lời giải và đáp án
Phép tính \(x - 5\) thực hiện được khi
-
A.
\(x < 5\)
-
B.
\(x \ge 5\)
-
C.
\(x < 4\)
-
D.
\(x = 3\)
Đáp án : B
Phép tính \(a - b\) thực hiện được khi \(a \ge b.\)
Phép tính \(x - 5\) thực hiện được khi \(x \ge 5.\)
Cho phép tính \(231 - 87\). Chọn câu đúng.
-
A.
\(231\) là số trừ
-
B.
\(87\) là số bị trừ
-
C.
\(231\) là số bị trừ
-
D.
\(87\) là hiệu
Đáp án : C
Trong phép trừ $a - b = x$ thì \(a\) là số bị trừ; \(b\) là số trừ và \(x\) là hiệu.
Trong phép trừ \(231 - 87\) thì \(231\) là số bị trừ và \(87\) là số trừ nên C đúng.
Cho phép tính \(x:3 = 6\), khi đó thương của phép chia là
-
A.
\(x\)
-
B.
\(6\)
-
C.
\(3\)
-
D.
\(18\)
Đáp án : B
Ta sử dụng (số bị chia) : (số chia) = (thương) để xác định thương của phép chia
Phép chia \(x:3 = 6\) có \(x\) là số bị chia; \(3\) là số chia và \(6\) là thương.
Nên thương của phép chia là \(6.\)
Tính 1 454-997
-
A.
575
-
B.
567
-
C.
457
-
D.
754
Đáp án : C
- Thêm vào số bị trừ và số trừ cùng một số sao cho số trừ mới là số tròn chục, tròn trăm, tròn nghìn.
- Tính: (số bị trừ mới) – (số trừ mới).
1 454-997 = (1 454+3)-(997+3)
= 1 457-1 000=457
Trong phép chia có dư \(a\) chia cho \(b,\) trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\) duy nhất sao cho:
\(a = b.q + r\)
Khẳng định nào sau đây đúng ?
-
A.
\(r \ge b\)
-
B.
\(0 < b < r\)
-
C.
\(0 < r < b\)
-
D.
\(0 \le r < b\)
Đáp án : C
Định nghĩa về phép chia hết và phép chia có dư.
Khi chia a cho b, trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\) duy nhất sao cho:
\(a = b.q + r\) trong đó \(0 \le r < b\)
Phép chia a cho b là phép chia có dư nên \(r \ne 0\)
Vậy \(0 < r < b\) .
Biểu diễn phép chia \(445:13\) dưới dạng \(a = b.q + r\) trong đó \(0 \le r < b\)
-
A.
\(445 = 13.34 + 3\)
-
B.
\(445 = 13.3 + 34\)
-
C.
\(445 = 34.3 + 13\)
-
D.
\(445 = 13.34\)
Đáp án : A
Đặt tính rồi tính.
Xác định a,b,q,r trong phép chia vừa nhận được.

Số bị chia là \(b = 445\), số chia là \(b = 13\) thương \(q = 34\), số dư là \(r = 3\). Ta biểu diễn phép chia như sau: \(445 = 13.34 + 3\)
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Đáp án : C
Đặt tính rồi tính.
Đếm số các phép chia có dư.
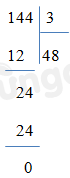

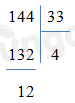

Vậy có 3 phép chia có dư
-
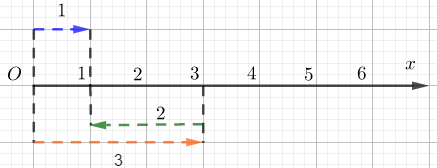
A.
Phép cộng của 1 và 2
-
B.
Phép trừ của 3 và 2
-
C.
Phép cộng của 1 và 3
-
D.
Phép trừ của 3 và 1
Đáp án : B
Số 3 và số 1 cùng chiều từ trái sang phải, số 2 ngược chiều với hai số này. Mà ta có 3-2=1 nên hình ảnh trên minh họa cho phép trừ 3-2.
Dạng tổng quát của số tự nhiên chia hết cho \(3\) là:
-
A.
\(3k\,\left( {k \in N} \right)\)
-
B.
\(5k + 3\,\left( {k \in N} \right)\)
-
C.
\(3k + 1\,\left( {k \in N} \right)\)
-
D.
\(3k + 2\,\left( {k \in N} \right)\)
Đáp án : A
Sử dụng các số hạng chia hết cho \(a\) có dạng $x = a.k\,\left( {k \in N} \right)$
Các số hạng chia hết cho \(3\) có dạng tổng quát là \(x = 3k\,\left( {k \in N} \right)\)
Dạng tổng quát của số tự nhiên chia cho \(5\) dư \(2\) là
-
A.
\(2k + 5\,\left( {k \in N} \right)\)
-
B.
\(5k + 2\,\left( {k \in N} \right)\)
-
C.
\(2k\,\left( {k \in N} \right)\)
-
D.
\(5k + 4\,\left( {k \in N} \right)\)
Đáp án : B
Số tự nhiên \(a\) chia cho \(b\) được thương \(q\) và dư $r$ có dạng \(a = b.q + r.\)
Dạng tổng quát của số tự nhiên chia cho \(5\) dư \(2\) là \(a = 5k + 2\,\left( {k \in N} \right).\)
Tình nhanh \(49.15 - 49.5\) ta được kết quả là
-
A.
\(490\)
-
B.
\(49\)
-
C.
\(59\)
-
D.
\(4900\)
Đáp án : A
Sử dụng tính chất phân phối của phép nhân với phép trừ \(ab - ac = a\left( {b - c} \right).\)
Ta có \(49.15 - 49.5\)\( = 49.\left( {15 - 5} \right) = 49.10 = 490.\)
Kết quả của phép tính $12.100 + 100.36 - 100.19$ là
-
A.
\(29000\)
-
B.
\(3800\)
-
C.
\(290\)
-
D.
\(2900\)
Đáp án : D
Sử dụng tính chất phân phối của phép nhân với phép cộng; phép trừ \(ab + ac - ad = a\left( {b + d - c} \right).\)
Ta có $12.100 + 100.36 - 100.19$\( = 100.\left( {12 + 36 - 19} \right) = 100.29 = 2900.\)