Trắc nghiệm Các dạng toán về bội chung, bội chung nhỏ nhất Toán 6 Chân trời sáng tạo
Đề bài
Có bao nhiêu số có ba chữ số là bội chung của a và b, biết rằng BCNN(a,b)=300.
-
A.
1
-
B.
2
-
C.
3
-
D.
300
Tìm bội chung nhỏ nhất của: 7 và 13
-
A.
182
-
B.
91
-
C.
13
-
D.
1
54 và 108 có bội chung nhỏ nhất là
-
A.
54
-
B.
1
-
C.
108
-
D.
216
Thực hiện các phép tính sau:\(\dfrac{3}{8} + \dfrac{5}{{24}}\). Với kết quả là phân số tối giản.
-
A.
\(\dfrac{{14}}{{24}}\)
-
B.
\(\dfrac{7}{{12}}\)
-
C.
\(\dfrac{{112}}{{192}}\)
-
D.
\(\dfrac{{12}}{7}\)
Cho tập hợp $X$ là ước của $35$ và lớn hơn $5$. Cho tập $Y$ là bội của $8$ và nhỏ hơn $50$.
Gọi $M$ là giao của $2$ tập hợp $X$ và $Y$, tập hợp $M$ có bao nhiêu phần tử?
-
A.
$2$
-
B.
$1$
-
C.
$0$
-
D.
$3$
Có bao nhiêu số tự nhiên \(x\) khác \(0\) thỏa mãn $x \in BC(12 ; 15 ; 20) $ và $x$ $ \le $ $100$
-
A.
$4$
-
B.
$3$
-
C.
$2$
-
D.
$1$
Tìm số tự nhiên \(x\) nhỏ nhất biết \(x \, \vdots \, 45;\,x \, \vdots \, 110\) và \(x \, \vdots \,75.\)
-
A.
$1650$
-
B.
$3750$
-
C.
$4950$
-
D.
$3300$
Tìm một số tự nhiên biết tích của ước số lớn nhất với bội số nhỏ nhất khác $0$ của nó là $256 .$
-
A.
$16$
-
B.
$18$
-
C.
$24$
-
D.
$32$
Một trường tổ chức cho học sinh đi tham quan bằng ôtô. Nếu xếp \(35\) hay \(40\) học sinh lên một ô tô thì đều thấy thiếu mất \(5\) ghế ngồi. Tính số học sinh đi tam quan biết số lượng học sinh đó trong khoảng từ \(800\) đến \(900\) em.
-
A.
$845$
-
B.
$840$
-
C.
$860$
-
D.
$900$
Chị Hòa có một số bông sen. Nếu chị bó thành các bó gồm 3 bông, 5 bông hay 7 bông
thì đều vừa hết. Hỏi chị Hòa có bao nhiêu bông sen? Biết rằng chị Hòa có khoảng từ
200 đến 300 bông.
-
A.
210
-
B.
220
-
C.
230
-
D.
240
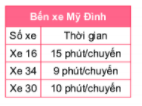
Lịch xuất bến của một số xe buýt tại bến xe Mỹ Đình (Hà Nội) được ghi ở bảng bên. Giả sử các xe buýt xuất bến cùng lúc vào 10 giờ 35 phút. Hỏi vào sau bao lâu thì cả 3 xe xuất bến cùng một lúc lần nữa (kể từ lần đầu tiên)?
-
A.
90 phút
-
B.
45 phút
-
C.
180 phút
-
D.
30 phút
Tìm số tự nhiên n lớn nhất có $3$ chữ số sao cho $n$ chia $8$ dư $7,$ chia $31$ dư $28.$
-
A.
$927$
-
B.
$183$
-
C.
$431$
-
D.
$729$
Cho \(a;b\) có \(BCNN\left( {a;b} \right) = 630;\,\)ƯCLN\(\left( {a;b} \right) = 18.\) Có bao nhiêu cặp số \(a;b\) thỏa mãn?
-
A.
$6$
-
B.
$5$
-
C.
$2$
-
D.
$3$
Tìm hai số tự nhiên $a,b\left( {a < b} \right).$ Biết $a + b = 20,BCNN\left( {a,b} \right) = 15.$
-
A.
$a = 15;b = 25.$
-
B.
$a = 15;b = 5.$
-
C.
$a = 15;b = 20.$
-
D.
$a = 5;b = 15.$
Một số tự nhiên \(a\) khi chia cho \(7\) dư \(4;\) chia cho \(9\) dư \(6.\) Tìm số dư khi chia \(a\) cho \(63.\)
-
A.
$0$
-
B.
$36$
-
C.
$3$
-
D.
$60$
Lời giải và đáp án
Có bao nhiêu số có ba chữ số là bội chung của a và b, biết rằng BCNN(a,b)=300.
-
A.
1
-
B.
2
-
C.
3
-
D.
300
Đáp án : C
- Bội chung của hai số a và b là bội của BCNN(a,b)
- Lấy BCNN(a,b) nhân với các số 1,2,3.
BCNN(a,b) = 300
BC(a,b) là bội của 300.
=> Tất cả các số có 3 chữ số là bội chung của a và b là: 300, 600, 900
Vậy có tất cả 3 số có ba chữ số là bội của a và b.
Tìm bội chung nhỏ nhất của: 7 và 13
-
A.
182
-
B.
91
-
C.
13
-
D.
1
Đáp án : B
- Bội chung nhỏ nhất của hai số nguyên tố cùng nhau là tích của hai số đó.
- Hai số a và b được gọi là hai số nguyên tố cùng nhau nếu ƯCLN(a,b)=1
Vì 7 và 13 đều là hai số nguyên tố nên ƯCLN(7,13)=1
Hay 7 và 13 là hai số nguyên tố cùng nhau.
=> BCNN(7,13) = 7 . 13 = 91.
54 và 108 có bội chung nhỏ nhất là
-
A.
54
-
B.
1
-
C.
108
-
D.
216
Đáp án : C
- Cách tìm BCNN:
+ Phân tích các số ra thừa số nguyên tố.
+ Chọn ra các thừa số nguyên tố chung và riêng.
+ Chọn lũy thừa với số mũ lớn nhất.
+ Lấy tích của các lũy thừa đã chọn.
$54={{2.3}^{3}}$
$108={{2}^{2}}{{.3}^{3}}$
Các thừa số chung của 54 và 108 là 2 và 3.
Số mũ lớn nhất của 2 là 2
Số mũ lớn nhất của 3 là 3.
\(BCNN(54,108)={{2}^{2}}{{.3}^{3}}=108\)
Thực hiện các phép tính sau:\(\dfrac{3}{8} + \dfrac{5}{{24}}\). Với kết quả là phân số tối giản.
-
A.
\(\dfrac{{14}}{{24}}\)
-
B.
\(\dfrac{7}{{12}}\)
-
C.
\(\dfrac{{112}}{{192}}\)
-
D.
\(\dfrac{{12}}{7}\)
Đáp án : B
- Để quy đồng mẫu hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\), ta phải tìm mẫu chung của hai phân số đó. Thông thường ta nên chọn mẫu chung là bội chung nhỏ nhất của hai mẫu.
- Để cộng, trừ các phân số khác mẫu ta đi quy đồng mẫu số các phân số rồi thực hiện cộng(trừ) tử số và giữ nguyên mẫu.
Ta có BCNN(8; 24) = 24 nên:
\(\dfrac{3}{8} + \dfrac{5}{{24}} = \dfrac{{3.3}}{{8.3}} + \dfrac{5}{{24}} = \dfrac{9}{{24}} + \dfrac{5}{{24}} = \dfrac{{14}}{{24}} = \dfrac{7}{{12}}\)
Cho tập hợp $X$ là ước của $35$ và lớn hơn $5$. Cho tập $Y$ là bội của $8$ và nhỏ hơn $50$.
Gọi $M$ là giao của $2$ tập hợp $X$ và $Y$, tập hợp $M$ có bao nhiêu phần tử?
-
A.
$2$
-
B.
$1$
-
C.
$0$
-
D.
$3$
Đáp án : C
- Áp dụng kiến thức ước (bội) của $1$ số, liệt kê tập hợp các ước (bội) số đó.
- So sánh với yêu cầu của đề bài, các ước (bội) lớn hơn (hay nhỏ hơn), để tìm ra tập hợp cuối cùng.
- Dựa vào kiến thức tập hợp để tìm ra tập hợp giao của $2$ tập hợp vừa tìm được.
Ư$(35) = \{ 1,5,7,35\} ;$Ư$(35) > 5 \Rightarrow X = \{ 7,35\} $
$B(8) = \{ 0,8,16,24,32,40,48,56,...\} $
$B(8) < 50 \Rightarrow Y = \{ 0,8,16,24,32,40,48\} $
Vì:
$X = \{ 7,35\} $
$Y = \{ 0,8,16,24,32,40,48\} $
$ \Rightarrow M = X \cap Y = \emptyset $ nên tập M không có phần tử nào.
Có bao nhiêu số tự nhiên \(x\) khác \(0\) thỏa mãn $x \in BC(12 ; 15 ; 20) $ và $x$ $ \le $ $100$
-
A.
$4$
-
B.
$3$
-
C.
$2$
-
D.
$1$
Đáp án : D
+ Tìm các bội số nhỏ hơn \(100\) của \(12;15;20.\)
+ Tìm các số chung cho cả ba số \(12;15;20\) trong bội số tìm được.
Ta có \(B\left( {12} \right) = \left\{ {0;12;24;36;48;60;72;84;96;...} \right\}\)
\(B\left( {15} \right) = \left\{ {0;15;30;45;60;75;90;105;...} \right\}\)
\(B\left( {20} \right) = \left\{ {0;20;40;60;80;100;...} \right\}\)
Nên \(BC\left( {12;15;20} \right) = \left\{ {0;60;120;...} \right\}\) mà \(x \le 100\) và \(x \ne 0\) nên \(x = 60.\)
Có một số tự nhiên thỏa mãn đề bài.
Tìm số tự nhiên \(x\) nhỏ nhất biết \(x \, \vdots \, 45;\,x \, \vdots \, 110\) và \(x \, \vdots \,75.\)
-
A.
$1650$
-
B.
$3750$
-
C.
$4950$
-
D.
$3300$
Đáp án : C
+ Từ đề bài suy ra \(x \in \)BC\(\left( {105;175;385} \right)\) mà \(x\) nhỏ nhất nên \(x = \) BCNN\(\left( {45;75;110} \right)\).
+ Tìm bội chung nhỏ nhất theo các bước
Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện theo ba bước sau :
Bước 1 : Phân tích mỗi số ra thừa số nguyên tố.
Bước 2 : Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3 : Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
Vì \(x \, \vdots \, 45;\,x \, \vdots \, 110\) và \(x \, \vdots \, 75\) nên \(x \, \in BC\left( {45;75;110} \right)\) mà \(x\) nhỏ nhất nên \(x = BCNN\left( {45;75;110} \right)\)
Ta có \(45 = {3^2}.5;\,75 = {3.5^2};\,110 = 2.5.11\)
Nên \(BCNN\left( {45;75;110} \right) = {2.3^2}{.5^2}.11\)\( = 4950.\)
Tìm một số tự nhiên biết tích của ước số lớn nhất với bội số nhỏ nhất khác $0$ của nó là $256 .$
-
A.
$16$
-
B.
$18$
-
C.
$24$
-
D.
$32$
Đáp án : A
Gọi số cần tìm là $a$ $( a \ne 0)$
Ta dùng kiến thức: " Bội nhỏ nhất của một số tự nhiên là chính nó, ước lớn nhất của một số tự nhiên khác $0$ cũng là chính nó" để lập luận và suy ra cách tính $a$.
Gọi số cần tìm là $a$ $( a \ne 0)$ Ước số lớn nhất của $a$ là $a$ Bội số nhỏ nhất khác $0$ của $a$ là $a$ Tích của ước số lớn nhất với bội số nhỏ nhất là: $a.a = 256 = {16^2}$ $ \Rightarrow a = 16.$
Vậy số cần tìm là \(16.\)
Một trường tổ chức cho học sinh đi tham quan bằng ôtô. Nếu xếp \(35\) hay \(40\) học sinh lên một ô tô thì đều thấy thiếu mất \(5\) ghế ngồi. Tính số học sinh đi tam quan biết số lượng học sinh đó trong khoảng từ \(800\) đến \(900\) em.
-
A.
$845$
-
B.
$840$
-
C.
$860$
-
D.
$900$
Đáp án : A
+ Sử dụng kiến thức về phép chia có dư.
+ Sử dụng kiến thức về bội chung và bội chung nhỏ nhất.
+ Sử dụng cách tìm bội chung thông qua bội chung nhỏ nhất.
Gọi số học sinh đi thăm quan là \(x\,\left( {x \in {N^*};\,800 \le x \le 900} \right)\) (học sinh)
Nếu xếp \(35\) hay \(40\) học sinh lên một ô tô thì đều thấy thiếu mất \(5\) ghế ngồi nghĩa là thừa ra 5 học sinh nên ta có
\(\left( {x - 5} \right) \vdots 35;\,\left( {x - 5} \right) \vdots 40\) suy ra \(\left( {x - 5} \right) \in BC\left( {35;40} \right)\).
Ta có \(35 = 5.7;\,40 = {2^3}.5\) nên \(BCNN\left( {35;40} \right) = {2^3}.5.7 = 280.\)
Suy ra \((x-5) \in BC\left( {35;40} \right) = B\left( {280} \right) = \left\{ {280;560;840;1120;...} \right\}\) mà \(800 \le x \le 900\) nên \(x -5= 840\) hay $x=845.$
Vậy số học sinh đi thăm quan là \(845\) học sinh.
Chị Hòa có một số bông sen. Nếu chị bó thành các bó gồm 3 bông, 5 bông hay 7 bông
thì đều vừa hết. Hỏi chị Hòa có bao nhiêu bông sen? Biết rằng chị Hòa có khoảng từ
200 đến 300 bông.
-
A.
210
-
B.
220
-
C.
230
-
D.
240
Đáp án : A
Số bông sen là bội chung của 3, 5, 7 và 200 < x < 300.
- Gọi số bông sen chị Hòa có là: x (bông, \(x \in \mathbb{N}\)).
- Nếu chị bó thành các bỏ bông gồm 3 bông, 5 bông hay 7 bông thì số bông sen chị Hòa có là bội chung của 3, 5 và 7.
- Theo đề bài ta có xe BC(3, 5, 7) và 200 < x < 300
Vì 3, 5, 7 từng đôi một là số nguyên tố cùng nhau.
=> BCNN(3, 5, 7) = 105
=> BC(3, 5, 7) = B(105) = {0; 105, 210, 315;...}
=> x\( \in \) BC(3, 5, 7) ={0, 105, 210, 315,.... }.
Mà \(200 \le x \le 300\) nên x = 210.
Vậy số bông sen chị Hòa có là 210 bông.
Lịch xuất bến của một số xe buýt tại bến xe Mỹ Đình (Hà Nội) được ghi ở bảng bên. Giả sử các xe buýt xuất bến cùng lúc vào 10 giờ 35 phút. Hỏi vào sau bao lâu thì cả 3 xe xuất bến cùng một lúc lần nữa (kể từ lần đầu tiên)?

-
A.
90 phút
-
B.
45 phút
-
C.
180 phút
-
D.
30 phút
Đáp án : A
- Tính xem cứ bao nhiêu phút thì các xe xuất bến cùng lúc: BCNN(15, 9, 10)
Thời gian các xe cùng xuất bến cách 10h35p các khoảng thời gian là BC(9, 10, 15)
Ta có: 9 = \({3^2}\), 10 = 2.5, 15 = 3.5.
Thừa số chung và riêng là 2, 3 và 5
Số mũ lớn nhất của 2 là 1
Số mũ lớn nhất của 3 là 2
Số mũ lớn nhất của 5 là 1
=> BCNN(9, 10, 15) = \({2.3^2}.5\) = 90
Vậy cứ 90 phút thì các xe xuất bến cùng một lúc.
Tìm số tự nhiên n lớn nhất có $3$ chữ số sao cho $n$ chia $8$ dư $7,$ chia $31$ dư $28.$
-
A.
$927$
-
B.
$183$
-
C.
$431$
-
D.
$729$
Đáp án : A
Bước 1: Vì $n$ chia $8$ dư $7,$ chia $31$ dư $28 $ nên: $\left( {n - 7} \right) \vdots 8$ và $\left( {n - 28} \right) \vdots 31$ $\left( {n > 28} \right)$ Bước 2 : Biến đổi tìm số tự nhiên $m$ sao cho $\left( {n + m} \right) \vdots 8$ và $\left( {n + m} \right) \vdots 31$ Khi đó $\left( {n + m} \right) \vdots BCNN\left( {8;31} \right)$ Bước 3: Tìm các giá trị của $n$ Chọn giá trị của $n$ thỏa mãn $n$ là số lớn nhất có $3$ chữ số
Vì $n$ chia $8$ dư $7$ nên $\left( {n - 7} \right) \vdots 8\,\,\,\,\left( {n > 7} \right)$ $ \Rightarrow n = 8a + 7$ với $a \in \mathbb{N}$$ \Rightarrow \left( {n + 1} \right) \vdots 8$
Vì $n$ chia $31$ dư $28$ nên $\left( {n - 28} \right) \vdots 31\left( {n > 28} \right)$ $ \Rightarrow n = 31b + 28$ $\left( {b \in \mathbb{N}} \right)$ $ \Rightarrow \left( {n + 3} \right) \vdots 31$ Vì $64 \vdots 8$ nên $\left( {n + 1 + 64} \right) \vdots 8$ hay $\left( {n + 65} \right) \vdots 8\left( 1 \right)$ Vì $62 \vdots 31$ $ \Rightarrow \left( {n + 3 + 62} \right) \vdots 31$ hay $\left( {n + 65} \right) \vdots 31$ (2) Từ (1) và (2) $ \Rightarrow \left( {n + 65} \right) \vdots $$BCNN\left( {8;31} \right)$ $ \Rightarrow \left( {n + 65} \right) \vdots 248$ $ \Rightarrow n = 248k - 65$ $\left( {k \in {\mathbb{N}^ * }} \right)$ Với $k = 1$ $ \Rightarrow n = 248.1 - 65 = 183$ Với $k = 2 \Rightarrow n = 248.2 - 65 = 431$ Với $k = 3 \Rightarrow n = 248.3 - 65 = 679$ Với $k = 4 \Rightarrow n = 248.4 - 65 = 927$ Với $k = 5 \Rightarrow n = 248.5 - 65 = 1175$ (loại) Vì $n$ là số lớn nhất có $3$ chữ số nên $n = 927.$
Cho \(a;b\) có \(BCNN\left( {a;b} \right) = 630;\,\)ƯCLN\(\left( {a;b} \right) = 18.\) Có bao nhiêu cặp số \(a;b\) thỏa mãn?
-
A.
$6$
-
B.
$5$
-
C.
$2$
-
D.
$3$
Đáp án : D
+ Vì ƯCLN\(\left( {a;b} \right) = 18\) nên đặt \(a = 18x;\,b = 18y\) với \(x;y \in N;\,\)\(ƯCLN\left( {x;y} \right) = 1;\,y \ne 1.\)
+ Sử dụng ƯCLN\(\left( {a;b} \right).BCNN\left( {a;b} \right) = a.b\) để tìm ra các giá trị \(x;y\) thỏa mãn từ đó suy ra các cặp số \(a;b\) cần tìm.
Vì ƯCLN\(\left( {a;b} \right) = 18\) nên đặt \(a = 18x;\,b = 18y\) với \(x;y \in N;\,\)\(ƯCLN \left( {x;y} \right) = 1;\,y \ne 1.\)
Vì ƯCLN\(\left( {a;b} \right).BCNN\left( {a;b} \right) = a.b\)
Nên \(18.630 = 18x.18y\) \( \Rightarrow x.y = \left( {18.630} \right):\left( {18.18} \right)\) hay \(x.y = 35\) mà \(y \ne 1\)
Do đó ta có:
+) Nếu \(x = 1\) thì \(y = 35\) khi đó \(a = 18.1 = 18;b = 35.18 = 630\)
+) Nếu \(x = 5\) thì \(y = 7\) khi đó \(a = 18.5 = 90;b = 7.18 = 126\)
+) Nếu \(x = 7\) thì \(y = 5\) khi đó \(a = 18.7 = 126;b = 5.18 = 90\)
Vậy có ba cặp số \(a;b\) thỏa mãn.
Tìm hai số tự nhiên $a,b\left( {a < b} \right).$ Biết $a + b = 20,BCNN\left( {a,b} \right) = 15.$
-
A.
$a = 15;b = 25.$
-
B.
$a = 15;b = 5.$
-
C.
$a = 15;b = 20.$
-
D.
$a = 5;b = 15.$
Đáp án : D
Gọi ƯCLN$\left( {a,b} \right) = d$ Tìm $d \in $ ƯC$\left( {15;20} \right)$ sau đó thay $d$ vào công thức $a.b = $ƯCLN$\left( {a,b} \right).BCNN\left( {a,b} \right),$ kết hợp điều kiện $a + b = 20$ để tìm $a$ và $b$.
Gọi ƯCLN$\left( {a,b} \right) = d$ $ \Rightarrow a = d.m,b = d.n;\left( {m,n} \right) = 1$ $ \Rightarrow a + b = d\left( {m + n} \right)$ $ \Rightarrow d \in $ Ư$\left( {a + b} \right)$ hay $d \in $Ư$\left( {20} \right)$ Vì $BCNN\left( {a,b} \right) = 15$ \( \Rightarrow 15 \vdots d\) hay $d \in $Ư$\left( {15} \right)$ $ \Rightarrow d \in $ ƯC$\left( {15;20} \right)$ Mà ƯCLN$\left( {15;20} \right) = 5$ nên $d = 1$ hoặc $d = 5$ +) Nếu $d = 1 \Rightarrow a.b = 1.15 = 15 = 3.5$ Khi đó $a + b = 3 + 5 = 8$ (loại) Hoặc $a + b = 1 + 15 = 16$ (loại) +) Nếu $d = 5$ thì $a.b = 5.15 = 75 = 1.75$ Khi đó $a + b = 15 + 5 = 20$ (thỏa mãn) Hoặc $a + b = 1 + 75 = 76$ (loại) Vậy hai số cần tìm là $a = 5;b = 15.$
Một số tự nhiên \(a\) khi chia cho \(7\) dư \(4;\) chia cho \(9\) dư \(6.\) Tìm số dư khi chia \(a\) cho \(63.\)
-
A.
$0$
-
B.
$36$
-
C.
$3$
-
D.
$60$
Đáp án : D
+ Sử dụng kiến thức về phép chia có dư.
+ Sử dụng kiến thức về bội chung và bội chung nhỏ nhất.
Vì \(a\) chia cho \(7\) dư \(4 \Rightarrow \left( {a + 3} \right) \vdots 7\)
\(a\) chia cho \(9\) dư \(6\) \( \Rightarrow \left( {a + 3} \right) \vdots 9\)
Do đó \(\left( {a + 3} \right) \in BC\left( {7;9} \right)\) mà \(BCNN\left( {7;9} \right) = 63.\)
Do đó \(\left( {a + 3} \right) \vdots 63 \Rightarrow a\) chia cho \(63\) dư \(60.\)