Trắc nghiệm Bài 9. Chuyển động thẳng biến đổi đều - Vật lí 10 Kết nối tri thức
Đề bài
Chuyển động thẳng biến đổi đều là chuyển động như thế nào?
-
A.
Chuyển động có quỹ đạo là đường thẳng
-
B.
Chuyển động thẳng mà vận tốc có độ lớn tăng hoặc giảm theo thời gian
-
C.
Chuyển động thẳng mà có quãng đường thay đổi theo thời gian
-
D.
Cả A và B đều đúng
Trong chuyển động thẳng biến đổi đều, đại lượng nào có độ lớn không đổi theo thời gian?
-
A.
Gia tốc
-
B.
Vận tốc
-
C.
Quãng đường
-
D.
Cả A và B
Biểu thức tính gia tốc a nào dưới đây đúng?
-
A.
\(a = \frac{{\Delta v}}{{\Delta t}}\)
-
B.
\(a = \frac{{\Delta v}}{{{{(\Delta t)}^2}}}\)
-
C.
\(a = \frac{{{{(\Delta v)}^2}}}{{\Delta t}}\)
-
D.
\(a = \frac{{\Delta s}}{{\Delta t}}\)
Một vật đang đứng yên bắt đầu chuyển động nhanh dần đều, sau 30 s thì vật đạt vận tốc 54 km/h. Gia tốc của vật chuyển động là bao nhiêu?
-
A.
2 m/s 2
-
B.
0,5 m/s 2
-
C.
1,8 m/s 2
-
D.
0,6 m/s 2
Một vật chuyển động nhanh dần đều với gia tốc là 5 m/s 2 . Biết ban đầu vật có vận tốc là 6 m/s. Biểu thức vận tốc tức thời của chuyển động trên là:
-
A.
v = -5 + 6.t
-
B.
v = 5 – 6.t
-
C.
v = 5 + 6.t
-
D.
v = 6 + 5.t
-
A.
25 m
-
B.
45 m
-
C.
15m
-
D.
85 m
-
A.
25 m
-
B.
45 m
-
C.
15m
-
D.
85 m
-
A.
25 m
-
B.
45 m
-
C.
15m
-
D.
85 m
-
A.
25 m
-
B.
45 m
-
C.
15m
-
D.
85 m
Chọn câu sai: Khi một chất điểm chuyển động thẳng biến đổi điều thì nó:
-
A.
Có gia tốc không đổi
-
B.
Có vận tốc không đổi
-
C.
Chỉ có thể chuyển động nhanh dần đều hoặc chậm dần đều.
-
D.
Có thể lúc đầu chuyển động chậm dần đều, sau đó chuyển động nhanh dần đều.
Câu nào dưới đây nói về chuyển động thẳng biến đổi đều là không đúng ?
-
A.
Vận tốc tức thời của vật chuyển động thẳng biến đổi đều có độ lớn tăng hay giảm đều theo thời gian.
-
B.
Gia tốc của vật chuyển động thẳng biến đổi đều luôn có độ lớn không đổi.
-
C.
Gia tốc của vật chuyển động thẳng biến đổi đều luôn cùng phương, cùng chiều với vận tốc.
-
D.
Quãng đường đi được của vật chuyển động thẳng biến đổi đều luôn được tính bằng công thức: \(s = {v_0}t + \frac{1}{2}a{t^2}\)
Hãy nêu đầy đủ các tính chất đặc trưng cho chuyển động thẳng nhanh dần đều
-
A.
Gia tốc của vật có độ lớn không đổi theo thời gian và luôn cùng phương, cùng chiều với véctơ vận tốc của vật.
-
B.
Vận tốc tức thời của vật có phương, chiều luôn không đổi và có độ lớn tăng theo hàm bậc nhất của thời gian.
-
C.
Quãng đường đi được của vật tăng theo hàm số bậc hai theo thời gian.
-
D.
Bao gồm các đặc điểm nêu trong các câu A , B và C.
Chọn câu sai? Chất điểm sẽ chuyển động thẳng nhanh dần đều nếu
-
A.
\(a > 0\) và \({v_0} > 0\)
-
B.
\(a > 0\) và \({v_0} = 0\)
-
C.
\(a < 0\) và \({v_0} > 0\)
-
D.
\(a < 0\) và \({v_0} = 0\)
Chuyển động thẳng biến đổi đều là chuyển động
-
A.
Có quỹ đạo là đường thẳng, có véctơ gia tốc và vận tốc không thay đổi trong suốt quá trình chuyển động.
-
B.
Có quỹ đạo là đường thẳng, véctơ gia tốc bằng không
-
C.
Có quỹ đạo là đường thẳng, véctơ gia tốc không thay đổi trong suốt quá trình chuyển động.
-
D.
Có quỹ đạo là đường thẳng, véctơ vận tốc không thay đổi trong suốt quá trình chuyển động.
Trong công thức tính quãng đường đi được của chuyển động thẳng chậm dần đều cho đến khi dừng lại: \(s = {v_0}t + \frac{1}{2}a{t^2}\) thì:
-
A.
\({v_0} < 0,a > 0,s < 0\)
-
B.
\({v_0} < 0,a > 0,s > 0\)
-
C.
\({v_0} > 0,a > 0,s > 0\)
-
D.
Cả A và C đúng
Chọn phát biểu sai ?
-
A.
Véctơ gia tốc của chuyển động thẳng biến đổi đều có phương không đổi.
-
B.
Véctơ gia tốc của chuyển động thẳng biến đổi đều có độ lớn không đổi.
-
C.
Véctơ gia tốc của chuyển động thẳng biến đổi đều cùng chiều với véctơ vận tốc.
-
D.
Véctơ gia tốc của chuyển động thẳng chậm dần đều ngược chiều với véctơ vận tốc.
Gia tốc là một đại lượng
-
A.
Đại số, đặc trưng nhanh hay chậm của chuyển động.
-
B.
Đại số, đặc trưng cho tính không thay đổi của vận tốc.
-
C.
Véctơ, đặc trưng cho tính nhanh hay chậm của chuyển động.
-
D.
Véctơ, đặc trưng cho sự thay đổi nhanh hay chậm của vận tốc.
Chọn câu đúng ?
-
A.
Trong chuyển động chậm dần đều gia tốc a < 0
-
B.
Trong chuyển động chậm dần đều với vận tốc v < 0
-
C.
Trong chuyển động nhanh dần đều vận tốc và gia tốc luôn dương.
-
D.
Trong chuyển động nhanh dần đều tích của vận tốc và gia tốc luôn dương.
Trong chuyển động chậm dần đều thì
-
A.
Gia tốc luôn có giá trị âm.
-
B.
Gia tốc luôn có giá trị dương.
-
C.
Gia tốc luôn có giá trị dương thì vật chuyển động ngược chiều dương.
-
D.
Cả A và C đều đúng.
Chọn câu đúng nhất?
-
A.
Gia tốc của chuyển động thẳng nhanh dần đều bao giờ cũng lớn hơn gia tốc của chuyển động thẳng chậm dần đều.
-
B.
Chuyển động thẳng nhanh dần đều có gia tốc lớn hơn thì có vận tốc lớn hơn.
-
C.
Chuyển động thẳng biến đổi đều có gia tốc tăng, giảm theo thời gian.
-
D.
Gia tốc của chuyển động thẳng nhanh dần đều có phương, chiều và độ lớn không đổi.
Xét một vật chuyển động trên một đường thẳng và không đổi hướng, gọi a là gia tốc, v o là vận tốc ban đầu, v là vận tốc tại thời điểm nào đó. Trong các kết luận sau, kết luận nào đúng?
-
A.
Nếu a > 0 và v 0 > 0 thì vật chuyển động nhanh dần đều.
-
B.
Nếu a < 0 và v 0 < 0 thì vật chuyển động nhanh dần đều.
-
C.
Nếu tích số a.v 0 > 0 thì vật chuyển động nhanh dần đều.
-
D.
Các kết luận A, B và C đều đúng.
Nếu chọn chiều dương là chiều chuyển động thì:
-
A.
Véctơ gia tốc của chuyển động thẳng nhanh dần đều hướng theo chiều dương.
-
B.
Véctơ vận tốc của chuyển động thẳng chậm dần đều hướng theo chiều dương.
-
C.
Véctơ gia tốc của chuyển động thẳng chậm dần đều hướng theo chiều dương.
-
D.
Câu A và B đều đúng.
Chuyển động thẳng biến đổi đều là chuyển động có
-
A.
Tốc độ không đổi.
-
B.
Véctơ vận tốc thay đổi theo thời gian.
-
C.
Véctơ vận tốc bằng không.
-
D.
Gia tốc không đổi theo thời gian.
Chọn phát biểu sai ?
-
A.
Véctơ gia tốc trong chuyển động thẳng có cùng phương với véctơ vận tốc.
-
B.
Véctơ vận tốc tức thời tại một điểm có phương tiếp tuyến với quỹ đạo với chuyển động tại điểm đó.
-
C.
Độ lớn gia tốc của chuyển động thẳng biến đổi đều luôn không đổi.
-
D.
Trong chuyển động thẳng chậm dần đều véctơ vận tốc và véctơ gia tốc cùng chiều với nhau.
Phát biểu nào sau đây là đúng nhất khi nói về khái niệm gia tốc?
-
A.
Gia tốc là đại lượng vật lý đặc trưng cho sự biến thiên nhanh hay chậm của vận tốc.
-
B.
Độ lớn của gia tốc đo bằng thương số giữa độ biến thiên của vận tốc và khoảng thời gian xảy ra sự biến thiên đó.
-
C.
Gia tốc là một đại lượng véctơ.
-
D.
Cả ba câu trên đều đúng.
Trong công thức liên hệ giữa quãng đường đi được, vận tốc và gia tốc của chuyển động nhanh dần đều \({v^2} - v_0^2 = 2{\rm{as}}\), ta có các điều kiện nào sau đây?
-
A.
\(s > 0;a > 0;v > {v_0}\)
-
B.
\(s < 0;a < 0;v < {v_0}\)
-
C.
\(s > 0;a > 0;v < {v_0}\)
-
D.
\(s > 0;a < 0;v > {v_0}\)
Chọn câu đúng ?
Từ các phương trình vận tốc cho biết tính chất các chuyển động sau
-
A.
\(v = 5 + 2t\) => vật chuyển động thẳng đều.
-
B.
\(v = 3t\) => vật chuyển động chậm dần đều.
-
C.
\(v = - 2t + 9\) => vật chuyển động nhanh dần đều.
-
D.
\(v = 6t\) => vật chuyển động nhanh dần đều.
Đặc điểm nào sau đây sai với chuyển động thẳng nhanh dần đều?
-
A.
Hiệu quãng đường đi được trong những khoảng thời gian liên tiếp luôn là hằng số.
-
B.
Vận tốc của vật luôn dương.
-
C.
Quãng đường đi biến đổi theo hàm bậc hai của thời gian.
-
D.
Vận tốc biến đổi theo hàm số bậc nhất của thời gian.
Chọn đáp án sai? Chất điểm chuyển động thẳng theo một chiều với gia tốc \(a = 4m/{s^2}\) có nghĩa là:
-
A.
Lúc đầu vận tốc bằng $0$ thì sau $1s$ sau vận tốc của nó bằng $4 m/s$.
-
B.
Lúc đầu vận tốc bằng $2 m/s$ thì sau $1 s$ sau vận tốc của nó bằng $6 m/s$.
-
C.
Lúc đầu vận tốc bằng $2 m/s$ thì sau $2 s$ sau vận tốc của nó bằng $8 m/s$.
-
D.
Lúc đầu vận tốc bằng $4 m/s$ thì sau $2 s$ sau vận tốc của nó bằng $12 m/s$.
Phương trình chuyển động của một vật trên một đường thẳng có dạng \(x = 2{t^2} + 10t + 100(m;s)\).Thông tin nào sau đây là đúng?
-
A.
Vật chuyển động nhanh dần đều với gia tốc a = 2 m/s 2
-
B.
Vật chuyển động chậm dần đều với gia tốc a = 4 m/s 2
-
C.
Tọa độ của vật lúc t = 0 là 100 m
-
D.
Vận tốc của vật tại thời điểm t là v = 10 m/s
Phương trình chuyển động của một vật trên một đường thẳng có dạng \(x = 4{t^2} - 3t + 7(m;s)\). Điều nào sau đây là sai ?
-
A.
Gia tốc $a = 4m/{s^2}$
-
B.
Tọa độ ban đầu \({x_0} = 7m\)
-
C.
Gia tốc $a = 8m/{s^2}$
-
D.
Vận tốc ban đầu ${v_0} = - 3m/s$
Đồ thị tọa độ theo thời gian của chất điểm chuyển động thẳng biến đổi đều có dạng
-
A.
Là đường thẳng song song với trục Ot
-
B.
Là đường thẳng có thể đi qua gốc tọa độ
-
C.
Là một nhánh parabol
-
D.
Là đường thẳng song song với trục Ox
Đồ thị v - t nào sau đây là đồ thị trong đó a > 0
-
A.

-
B.
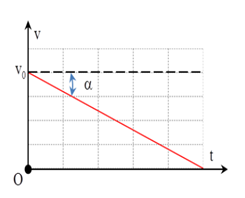
-
C.
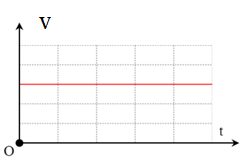
-
D.

Đồ thị a - t của chuyển động thẳng biến đổi đều có dạng:
-
A.
Là đường thẳng song song với trục Ot
-
B.
Là đường thẳng có thể đi qua gốc tọa độ
-
C.
Là một nhánh parabol
-
D.
Là đường thẳng song song với trục Ox
Một đoàn tàu bắt đầu rời ga. Chuyển động nhanh dần đều, sau $20s$ đạt đến vận tốc $36km/h$ . Hỏi sau bao lâu nữa tàu đạt được vận tốc $54km/h$?
-
A.
$t = 30s$
-
B.
$t = 5s$
-
C.
$t = 10s$
-
D.
$t = 20s$
Một vật chuyển động thẳng có phương trình \(x = 30 + 4t - {t^2}(m;s)\) . Tính quãng đường vật đi từ thời điểm $t_1 = 1s$ đến thời điểm $t_2 = 3s$?
-
A.
$2m$
-
B.
$0$
-
C.
$4m$
-
D.
Một đáp án khác
Một vật đang chuyển động với vận tốc $36km/h$ , tài xế tắt máy và hãm phanh xe chuyển động chậm dần đều sau $50m$ nữa thì dừng lại. Quãng đường xe đi được trong $4s$ kể từ lúc bắt đầu hãm phanh là:
-
A.
20m
-
B.
32m
-
C.
18m
-
D.
2,5m
Một vật chuyển động thẳng có phương trình vận tốc \(v = 2 - 2t\).Tốc độ trung bình của vật sau $4s$ kể từ lúc bắt đầu chuyển động là:
-
A.
-2m/s
-
B.
12m/s
-
C.
-12m/s
-
D.
2,5m/s
Một vật chuyển động thẳng nhanh dần đều, trong giây thứ hai vật đi được quãng đường dài $1,5m$. Tính quãng đường vật đi được trong giây thứ $100$?
-
A.
$199m$
-
B.
$200m$
-
C.
$99,5m$
-
D.
$210,5m$
Phương trình nào sau đây cho biết vật chuyển động nhanh dần đều dọc theo chiều dương của trục x?
-
A.
\(x = 10 - 5t - 0,5{t^2}\)
-
B.
\(x = 10 - 5t + 0,5{t^2}\)
-
C.
\(x = 10 + 5t + 0,5{t^2}\)
-
D.
\(x = 10 + 5t - 0,5{t^2}\)
Vật chuyển động thẳng có phương trình \(x = 2{t^2} - 4t + 10(m;s)\) . Vật sẽ dừng lại tại vị trí :
-
A.
x = 10m
-
B.
x = 4m
-
C.
x = 6m
-
D.
x = 8m
Phương trình chuyển động của một vật có dạng \(x = 3 - 4t + 2{t^2}(m;s)\). Biểu thức vận tốc tức thời của vật theo thời gian là:
-
A.
\(v = 2(t - 2)m/s\)
-
B.
\(v = 4(t - 1)m/s\)
-
C.
\(v = 2(t - 1)m/s\)
-
D.
\(v = 2(t + 2)m/s\)
Một vật chuyển động nhanh dần đều với vận tốc ban đầu $v_0 = 0$. Trong giây thứ nhất vật đi được quãng đường $s_1 = 3m$. Trong giây thứ hai vật đi được quãng đường $s_2$ bằng:
-
A.
$3m$
-
B.
$36m$
-
C.
$12m$
-
D.
Một đáp án khác.
Một ôtô đang chuyển động với vận tốc $54km/h$ thì hãm phanh, chuyển động chậm dần đều và dừng lại sau $10s$. Chọn chiều dương là chiều chuyển động của ôtô .Vận tốc của ôtô sau khi hãm phanh được $6s$ là:
-
A.
2,5m/s
-
B.
6m/s
-
C.
7,5m/s
-
D.
9m/s.
Một chiếc xe hơi giảm tốc chậm dần đều từ $54km/h$ còn $36km/h$ trên quãng đường thẳng dài $125m$. Vậy gia tốc của xe trên đoạn đường này là:
-
A.
-1,480m/s 2
-
B.
-0,072m/s 2
-
C.
-0,500m/s 2
-
D.
-1,000m/s 2
Một xe ôtô chuyển động chậm dần đều với vận tốc ban đầu \(v_0= 20m/s\) và gia tốc \(3m/s^2\). Vận tốc của xe khi đi thêm \(50m\) và quãng đường đi được cho đến khi dừng lại hẳn lần lượt có giá trị là:
-
A.
12,37m/s; 150m
-
B.
10m/s; 66,7m
-
C.
13,72m/s; 150m.
-
D.
13,27m/s; 200m .
Một đoàn tàu đang chạy với vận tốc 72km/h thì hãm phanh, chạy chậm dần đều sau 10s vận tốc giảm xuống còn 54km/h . Hỏi sau bao lâu thì tàu dừng lại hẳn
-
A.
Sau 55s từ lúc hãm phanh.
-
B.
Sau 50s từ lúc hãm phanh.
-
C.
Sau 45s từ lúc hãm phanh
-
D.
Sau 40s từ lúc hãm phanh
Lúc 7 h, hai ôtô bắt đầu khởi hành từ hai điểm A, B cách nhau 2400 m, chuyển động nhanh dần đều và ngược chiều nhau. ôtô đi từ A có gia tốc 1 m/s 2 , còn ôtô từ B có gia tốc 2 m/s 2 . Chọn chiều dương hướng từ A đến B, gốc thời gian lúc 7 h. Xác định vị trí hai xe gặp nhau:
-
A.
1600m
-
B.
1200m
-
C.
800m
-
D.
2400m
Cùng một lúc tại hai điểm $A, B$ cách nhau $125 m$ có hai vật chuyển động ngược chiều nhau. Vật đi từ $A$ có vận tốc đầu $4 m/s$ và gia tốc là $2 m/{s^2}$, vật đi từ B có vận tốc đầu $6 m/s$ và gia tốc $4 m/{s^2}$. Biết các vật chuyển động nhanh dần đều. Chọn $A$ làm gốc tọa độ, chiều dương hướng từ $A$ đến $B$, gốc thời gian lúc hai vật cùng xuất phát. Xác định thời điểm hai vật gặp nhau?
-
A.
10s
-
B.
5s
-
C.
6s
-
D.
12s
Một xe ôtô đi từ Ba La vào trung tâm Hà Nội có đồ thị v-t như hình vẽ:
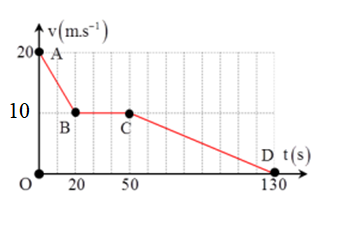
Quãng đường mà ôtô đi được là:
-
A.
$1km$
-
B.
$1,5km$
-
C.
$1,4km$
-
D.
$2km$
Cho đồ thị v - t của hai ôtô như hình vẽ:
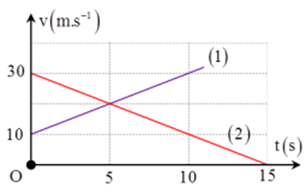
Giao điểm của đồ thị cho biết:
-
A.
Thời điểm 2 xe gặp nhau
-
B.
Thời điểm 2 xe có cùng tốc độ
-
C.
Khoảng cách 2 xe gặp nhau
-
D.
Cả A và B
Cho đồ thị v - t của hai ôtô như hình vẽ:
Chọn phương án đúng ?
-
A.
\({v_1} = 10 - 2t\)
-
B.
\({v_2} = 30 - 2t\)
-
C.
\({v_2} = 30 + 2t\)
-
D.
\({v_2} = 10 - 1,5t\)
Một chất điểm chuyển động thẳng có đồ thị vận tốc - thời gian như hình vẽ. Trong suốt quá trình chuyển động, tốc độ trung bình là 9 m/s. Phương trình chuyển động của chất điểm khi đi từ B đến C là?
-
A.
\(x = 24 + 12(t - 4)\)
-
B.
\(x = 1,5{t^2}\)
-
C.
\(x = 96 + 12(t - 10) - 3{(t - 10)^2}\)
-
D.
\(x = 24 + 12t - 3{t^2}\)
Ba vật chuyển động thẳng có đồ thị v - t như hình vẽ:

Sau bao nhiêu giây thì vật thứ 3 sẽ dừng lại?
-
A.
5s
-
B.
1s
-
C.
2s
-
D.
3s
Một vật chuyển động thẳng chậm dần đều với tốc độ đầu \(3m/s\) và gia tốc \(2m/s^2,\) thời điểm ban đầu ở gốc toạ độ và chuyển động ngược chiều dương của trục toạ độ thì phương trình có dạng.
-
A.
\(x = 3t + t^2\)
-
B.
\(x = -3t - 2t^2\)
-
C.
\(x = -3t + t^2\)
-
D.
\(x = 3t - t^2\)
Phương trình của một vật chuyển động thẳng là : \(x = 6 + 12t + {t^2}{\mkern 1mu} {\mkern 1mu} \left( {cm;s} \right)\)
a) Xác định gia tốc và vận tốc ban đầu của vật?
b) Viết công thức vận tốc và tính vận tốc của vật sau \(2s\) kể từ thời điểm ban đầu.
-
A.
\(a)\,{v_0} = 12cm/s;a = 2cm/{s^2}\,\,\,b)\,16cm/s\)
-
B.
\(a)\,{v_0} = 6cm/s;a = 1cm/{s^2}\,\,\,b)\,6cm/s\)
-
C.
\(a)\,{v_0} = 6cm/s;a = 12cm/{s^2}\,\,\,b)\,30cm/s\)
-
D.
\(a)\,{v_0} = 12cm/s;a = 6cm/{s^2}\,\,\,b)\,24cm/s\)
Một xe chuyển động nhanh dần đều đi được S = 24m, S 2 = 64m trong 2 khoảng thời gian liên tiếp bằng nhau là 4s. Xác định vận tốc ban đầu và gia tốc.
-
A.
\({v_{01}} = 1m/s,\;a = 2,5m/{s^2}\)
-
B.
\({v_{01}} = 1m/s,\;a = 2m/{s^2}\)
-
C.
\({v_{01}} = 1m/s,\;a = 3,5m/{s^2}\)
-
D.
\({v_{01}} = 1,5m/s,\;a = 2,5m/{s^2}\)
Hai người đi xe đạp khởi hành cùng một lúc từ 2 địa điểm A và B, đi ngược chiều nhau. Người đi từ A có vận tốc đầu là \(18km/h\) và chuyển động chậm dần đều với gia tốc \(20cm/{s^2}\). Người đi từ B có vận tốc đầu là \(5,4m/s\) và chuyển động nhanh dần đều với gia tốc\(0,2m/{s^2}\). Khoảng cách giữa hai người lúc đầu là \(130m\). Hỏi sau bao lâu 2 người gặp nhau và vị trí gặp nhau?
-
A.
\(t = 12,5s\); cách A \(83,125m\)
-
B.
\(t = 20s\); cách B \(60m\)
-
C.
\(t = 20s\); cách A \(60m\)
-
D.
\(t = 12,5s\); cách A \(46,875m\)
Một ô tô đang chuyển động với vận tốc 54km/h thì hãm phanh chuyển động chậm dần đều đi được 20m thì vận tốc còn 18km/h. Tính gia tốc của ô tô và quãng đường ô tô đi được từ lúc hãm phanh đến lúc dừng hẳn.
-
A.
\( - 5m/{s^2};\,\,22,5m\)
-
B.
\(5m/{s^2};\,\,22,5m\)
-
C.
\(3m/{s^2};\,\,30m\)
-
D.
\( - 3m/{s^2};\,\,30m\)
Lời giải và đáp án
Chuyển động thẳng biến đổi đều là chuyển động như thế nào?
-
A.
Chuyển động có quỹ đạo là đường thẳng
-
B.
Chuyển động thẳng mà vận tốc có độ lớn tăng hoặc giảm theo thời gian
-
C.
Chuyển động thẳng mà có quãng đường thay đổi theo thời gian
-
D.
Cả A và B đều đúng
Đáp án : B
Vận dụng lí thuyết đã học trong sách giáo khoa
Chuyển động thẳng biến đổi đều là chuyển động thẳng mà vận tốc có độ lớn tăng hoặc giảm đều theo thời gian.
Trong chuyển động thẳng biến đổi đều, đại lượng nào có độ lớn không đổi theo thời gian?
-
A.
Gia tốc
-
B.
Vận tốc
-
C.
Quãng đường
-
D.
Cả A và B
Đáp án : A
Vận dụng lí thuyết trong sách giáo khoa
Vì chuyển động thẳng biến đổi đều có vận tốc thay đều theo thời gian nên gia tốc của chuyển động này không đổi theo thời gian:
\(a = \frac{{\Delta v}}{{\Delta t}} = hs\)
Biểu thức tính gia tốc a nào dưới đây đúng?
-
A.
\(a = \frac{{\Delta v}}{{\Delta t}}\)
-
B.
\(a = \frac{{\Delta v}}{{{{(\Delta t)}^2}}}\)
-
C.
\(a = \frac{{{{(\Delta v)}^2}}}{{\Delta t}}\)
-
D.
\(a = \frac{{\Delta s}}{{\Delta t}}\)
Đáp án : A
Vận dụng kiến thức đã học
Biểu thức tính gia tốc trong chuyển động thẳng biến đổi đều là:
\(a = \frac{{\Delta v}}{{\Delta t}}\)
Trong đó:
+ Δv = v – v 0 : sự thay đổi vận tốc (m/s)
+ Δt = t – t 0 : thời gian vật chuyển động (s)
+ a: gia tốc (m/s 2 )
Một vật đang đứng yên bắt đầu chuyển động nhanh dần đều, sau 30 s thì vật đạt vận tốc 54 km/h. Gia tốc của vật chuyển động là bao nhiêu?
-
A.
2 m/s 2
-
B.
0,5 m/s 2
-
C.
1,8 m/s 2
-
D.
0,6 m/s 2
Đáp án : B
- Biểu thức tính gia tốc trong chuyển động thẳng biến đổi đều là:
\(a = \frac{{\Delta v}}{{\Delta t}}\)
Trong đó:
+ Δv = v – v 0 : sự thay đổi vận tốc (m/s)
+ Δt = t – t 0 : thời gian vật chuyển động (s)
+ a: gia tốc (m/s 2 )
- 1 m/s = 3,6 km/h
Đổi 54 km/h = 15 m/s.
Ban đầu vật đứng yên nên v 0 = 0.
Gia tốc của vật chuyển động là:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{15}}{{30}} = 0,5(m/{s^2})\)
Một vật chuyển động nhanh dần đều với gia tốc là 5 m/s 2 . Biết ban đầu vật có vận tốc là 6 m/s. Biểu thức vận tốc tức thời của chuyển động trên là:
-
A.
v = -5 + 6.t
-
B.
v = 5 – 6.t
-
C.
v = 5 + 6.t
-
D.
v = 6 + 5.t
Đáp án : D
Biểu thức vận tốc tức thời: v = v 0 + a.t
Ta có v 0 = 6 và a = 5 m/s 2
=> Biểu thức vận tốc tức thời của chuyển động là: v = v 0 + a.t = 6 + 5.t
-
A.
25 m
-
B.
45 m
-
C.
15m
-
D.
85 m
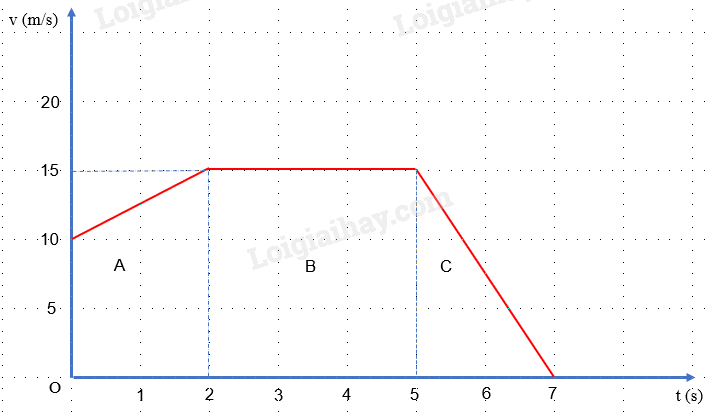
Đáp án : D
Độ dịch chuyển = Diện tích giới hạn của đồ thị v – t với trục hoành và trục tung
Độ dịch chuyển = S A + S B + S C
Diện tích của thang A là: \({S_A} = \frac{1}{2}.(10 + 15).2 = 25(m)\)
Diện tích hình chữ nhật B là: \({S_B} = 15.3 = 45(m)\)
Diện tích hình tam giác C là: \({S_C} = \frac{1}{2}.15.2 = 15(m)\)
=> Độ dịch chuyển: d = S A + S B + S C = 25 + 45 + 15 = 85 (m)
-
A.
25 m
-
B.
45 m
-
C.
15m
-
D.
85 m
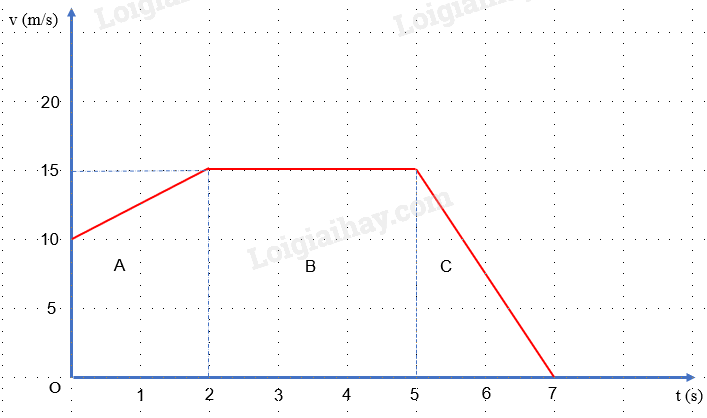
Đáp án : A
Độ dịch chuyển = Diện tích giới hạn của đồ thị v – t với trục hoành và trục tung
Độ dịch chuyển trong 2 s đầu = S A
Diện tích của thang A là: \({S_A} = \frac{1}{2}.(10 + 15).2 = 25(m)\)
-
A.
25 m
-
B.
45 m
-
C.
15m
-
D.
85 m
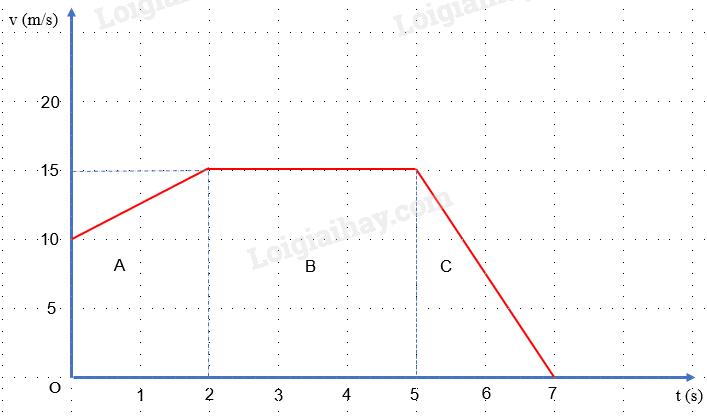
Đáp án : B
Độ dịch chuyển = Diện tích giới hạn của đồ thị v – t với trục hoành và trục tung
Độ dịch chuyển từ giây thứ 2 đến giây thứ 5 = S B
=> Diện tích hình chữ nhật B là: \({S_B} = 15.3 = 45(m)\)
-
A.
25 m
-
B.
45 m
-
C.
15m
-
D.
85 m
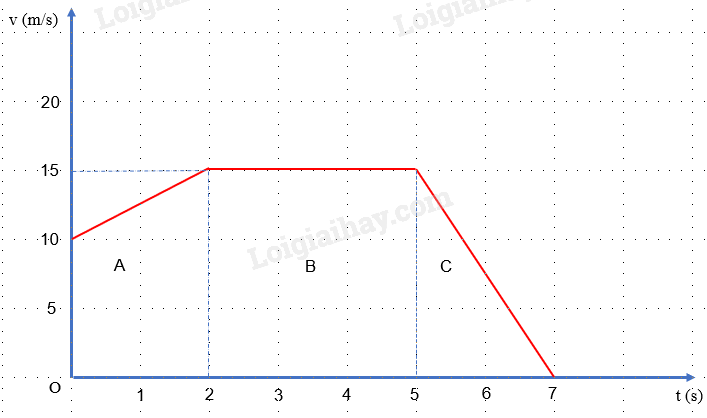
Đáp án : C
Độ dịch chuyển = Diện tích giới hạn của đồ thị v – t với trục hoành và trục tung
Độ dịch chuyển trong 2 s cuối = S C
=> Diện tích hình tam giác C là: \({S_C} = \frac{1}{2}.15.2 = 15(m)\)
Chọn câu sai: Khi một chất điểm chuyển động thẳng biến đổi điều thì nó:
-
A.
Có gia tốc không đổi
-
B.
Có vận tốc không đổi
-
C.
Chỉ có thể chuyển động nhanh dần đều hoặc chậm dần đều.
-
D.
Có thể lúc đầu chuyển động chậm dần đều, sau đó chuyển động nhanh dần đều.
Đáp án : B
A, C, D - đúng
B - sai vì trong chuyển động biến đổi đều vận tốc thay đổi theo phương trình: \(v = {v_0} + at\)
Câu nào dưới đây nói về chuyển động thẳng biến đổi đều là không đúng ?
-
A.
Vận tốc tức thời của vật chuyển động thẳng biến đổi đều có độ lớn tăng hay giảm đều theo thời gian.
-
B.
Gia tốc của vật chuyển động thẳng biến đổi đều luôn có độ lớn không đổi.
-
C.
Gia tốc của vật chuyển động thẳng biến đổi đều luôn cùng phương, cùng chiều với vận tốc.
-
D.
Quãng đường đi được của vật chuyển động thẳng biến đổi đều luôn được tính bằng công thức: \(s = {v_0}t + \frac{1}{2}a{t^2}\)
Đáp án : C
A, B, D - đúng
C- sai vì:
+ Khi vật chuyển động nhanh dần đều thì: Véctơ gia tốc và véctơ vận tốc luôn cùng hướng
+ Khi vật chuyển động chậm dần đều thì: Véctơ gia tốc và véctơ vận tốc luôn ngược hướng
Hãy nêu đầy đủ các tính chất đặc trưng cho chuyển động thẳng nhanh dần đều
-
A.
Gia tốc của vật có độ lớn không đổi theo thời gian và luôn cùng phương, cùng chiều với véctơ vận tốc của vật.
-
B.
Vận tốc tức thời của vật có phương, chiều luôn không đổi và có độ lớn tăng theo hàm bậc nhất của thời gian.
-
C.
Quãng đường đi được của vật tăng theo hàm số bậc hai theo thời gian.
-
D.
Bao gồm các đặc điểm nêu trong các câu A , B và C.
Đáp án : D
Các đặc trưng của chuyển động thẳng nhanh dần đều gồm cả A, B và C
Chọn câu sai? Chất điểm sẽ chuyển động thẳng nhanh dần đều nếu
-
A.
\(a > 0\) và \({v_0} > 0\)
-
B.
\(a > 0\) và \({v_0} = 0\)
-
C.
\(a < 0\) và \({v_0} > 0\)
-
D.
\(a < 0\) và \({v_0} = 0\)
Đáp án : C
Chất điểm chuyển động nhanh dần đều nếu a và v cùng dấu (a.v > 0)
=> Phương án C - sai vì: a.v 0 < 0
Chuyển động thẳng biến đổi đều là chuyển động
-
A.
Có quỹ đạo là đường thẳng, có véctơ gia tốc và vận tốc không thay đổi trong suốt quá trình chuyển động.
-
B.
Có quỹ đạo là đường thẳng, véctơ gia tốc bằng không
-
C.
Có quỹ đạo là đường thẳng, véctơ gia tốc không thay đổi trong suốt quá trình chuyển động.
-
D.
Có quỹ đạo là đường thẳng, véctơ vận tốc không thay đổi trong suốt quá trình chuyển động.
Đáp án : C
Chuyển động thẳng biến đổi là chuyển động thẳng trong đó gia tốc tức thời không đổi
- Ta để ý rằng khái niệm vectơ vận tốc không đổi nghĩa là trong suốt quá trình chuyển động cả độ lớn và phương chiều của vận tốc là không thay đổi điều này không phù hợp với chuyển động thẳng biến đổi đều có độ lớn vận tốc là một hàm bậc nhất của thời gian
Trong công thức tính quãng đường đi được của chuyển động thẳng chậm dần đều cho đến khi dừng lại: \(s = {v_0}t + \frac{1}{2}a{t^2}\) thì:
-
A.
\({v_0} < 0,a > 0,s < 0\)
-
B.
\({v_0} < 0,a > 0,s > 0\)
-
C.
\({v_0} > 0,a > 0,s > 0\)
-
D.
Cả A và C đúng
Đáp án : B
Trong chuyển động thẳng chậm dần đều thì vận tốc và gia tốc ngược dấu nhau, quãng đường là đại lượng không âm
Chọn phát biểu sai ?
-
A.
Véctơ gia tốc của chuyển động thẳng biến đổi đều có phương không đổi.
-
B.
Véctơ gia tốc của chuyển động thẳng biến đổi đều có độ lớn không đổi.
-
C.
Véctơ gia tốc của chuyển động thẳng biến đổi đều cùng chiều với véctơ vận tốc.
-
D.
Véctơ gia tốc của chuyển động thẳng chậm dần đều ngược chiều với véctơ vận tốc.
Đáp án : C
Trong chuyển động thẳng biến đổi đều thì + Gia tốc và vận tốc cùng phương, cùng chiều khi chuyển động này là nhanh dần đều + Gia tốc và vận tốc cùng phương, ngược chiều khi chuyển động này là chậm dần đều
Gia tốc là một đại lượng
-
A.
Đại số, đặc trưng nhanh hay chậm của chuyển động.
-
B.
Đại số, đặc trưng cho tính không thay đổi của vận tốc.
-
C.
Véctơ, đặc trưng cho tính nhanh hay chậm của chuyển động.
-
D.
Véctơ, đặc trưng cho sự thay đổi nhanh hay chậm của vận tốc.
Đáp án : D
Gia tốc là đại lượng vecto đặc trưng cho sự biến đổi nhanh hay chậm của vận tốc
Chọn câu đúng ?
-
A.
Trong chuyển động chậm dần đều gia tốc a < 0
-
B.
Trong chuyển động chậm dần đều với vận tốc v < 0
-
C.
Trong chuyển động nhanh dần đều vận tốc và gia tốc luôn dương.
-
D.
Trong chuyển động nhanh dần đều tích của vận tốc và gia tốc luôn dương.
Đáp án : D
Trong chuyển động nhanh dần đều tích của vận tốc và gia tốc luôn dương.
Trong chuyển động chậm dần đều thì
-
A.
Gia tốc luôn có giá trị âm.
-
B.
Gia tốc luôn có giá trị dương.
-
C.
Gia tốc luôn có giá trị dương thì vật chuyển động ngược chiều dương.
-
D.
Cả A và C đều đúng.
Đáp án : C
Trong chuyển động chậm dần đều khi gia tốc luôn có giá trị dương thì lúc đó vật chuyển động ngược chiều dương vì chuyển động chậm dần đều có a.v < 0.
=> Phương án C - đúng
A, B - sai vì: Gia tốc a có thể âm hoặc dương
Chọn câu đúng nhất?
-
A.
Gia tốc của chuyển động thẳng nhanh dần đều bao giờ cũng lớn hơn gia tốc của chuyển động thẳng chậm dần đều.
-
B.
Chuyển động thẳng nhanh dần đều có gia tốc lớn hơn thì có vận tốc lớn hơn.
-
C.
Chuyển động thẳng biến đổi đều có gia tốc tăng, giảm theo thời gian.
-
D.
Gia tốc của chuyển động thẳng nhanh dần đều có phương, chiều và độ lớn không đổi.
Đáp án : D
Gia tốc của chuyển động thẳng nhanh dần đều có phương, chiều và độ lớn không đổi.
Xét một vật chuyển động trên một đường thẳng và không đổi hướng, gọi a là gia tốc, v o là vận tốc ban đầu, v là vận tốc tại thời điểm nào đó. Trong các kết luận sau, kết luận nào đúng?
-
A.
Nếu a > 0 và v 0 > 0 thì vật chuyển động nhanh dần đều.
-
B.
Nếu a < 0 và v 0 < 0 thì vật chuyển động nhanh dần đều.
-
C.
Nếu tích số a.v 0 > 0 thì vật chuyển động nhanh dần đều.
-
D.
Các kết luận A, B và C đều đúng.
Đáp án : D
Trong chuyển động thẳng nhanh dần đều thì a và v luôn cùng dấu
Nếu chọn chiều dương là chiều chuyển động thì:
-
A.
Véctơ gia tốc của chuyển động thẳng nhanh dần đều hướng theo chiều dương.
-
B.
Véctơ vận tốc của chuyển động thẳng chậm dần đều hướng theo chiều dương.
-
C.
Véctơ gia tốc của chuyển động thẳng chậm dần đều hướng theo chiều dương.
-
D.
Câu A và B đều đúng.
Đáp án : D
Nếu chọn chiều dương là chiều chuyển động thì:
+ Véctơ gia tốc của chuyển động thẳng nhanh dần đều hướng theo chiều dương
+ Véctơ gia tốc của chuyển động thẳng chậm dần đều hướng ngược chiều dương
+ Véctơ vận tốc của chuyển động thẳng chậm dần đều và nhanh dần đều đều hướng theo chiều dương
Chuyển động thẳng biến đổi đều là chuyển động có
-
A.
Tốc độ không đổi.
-
B.
Véctơ vận tốc thay đổi theo thời gian.
-
C.
Véctơ vận tốc bằng không.
-
D.
Gia tốc không đổi theo thời gian.
Đáp án : D
Chuyển động thẳng biến đổi đều là chuyển động có gia tốc không đổi theo thời gian
Chọn phát biểu sai ?
-
A.
Véctơ gia tốc trong chuyển động thẳng có cùng phương với véctơ vận tốc.
-
B.
Véctơ vận tốc tức thời tại một điểm có phương tiếp tuyến với quỹ đạo với chuyển động tại điểm đó.
-
C.
Độ lớn gia tốc của chuyển động thẳng biến đổi đều luôn không đổi.
-
D.
Trong chuyển động thẳng chậm dần đều véctơ vận tốc và véctơ gia tốc cùng chiều với nhau.
Đáp án : D
Trong chuyển động chậm dần đều thì vectơ gia tốc và vận tốc ngược chiều nhau
Phát biểu nào sau đây là đúng nhất khi nói về khái niệm gia tốc?
-
A.
Gia tốc là đại lượng vật lý đặc trưng cho sự biến thiên nhanh hay chậm của vận tốc.
-
B.
Độ lớn của gia tốc đo bằng thương số giữa độ biến thiên của vận tốc và khoảng thời gian xảy ra sự biến thiên đó.
-
C.
Gia tốc là một đại lượng véctơ.
-
D.
Cả ba câu trên đều đúng.
Đáp án : D
Sử dụng lí thuyêt về gia tốc
Cả A, B, C đều đúng
Trong công thức liên hệ giữa quãng đường đi được, vận tốc và gia tốc của chuyển động nhanh dần đều \({v^2} - v_0^2 = 2{\rm{as}}\), ta có các điều kiện nào sau đây?
-
A.
\(s > 0;a > 0;v > {v_0}\)
-
B.
\(s < 0;a < 0;v < {v_0}\)
-
C.
\(s > 0;a > 0;v < {v_0}\)
-
D.
\(s > 0;a < 0;v > {v_0}\)
Đáp án : A
Công thức \({v^2} - v_0^2 = 2{\rm{as}}\) chỉ đúng khi chuyển động là không đổi chiều. Với v > v 0 => vật chuyển động theo chiều dương, chuyển động là nhanh dần nên a và v cùng chiều do vậy a > 0, quãng đường s là một đại lượng không âm
Chọn câu đúng ?
Từ các phương trình vận tốc cho biết tính chất các chuyển động sau
-
A.
\(v = 5 + 2t\) => vật chuyển động thẳng đều.
-
B.
\(v = 3t\) => vật chuyển động chậm dần đều.
-
C.
\(v = - 2t + 9\) => vật chuyển động nhanh dần đều.
-
D.
\(v = 6t\) => vật chuyển động nhanh dần đều.
Đáp án : D
Đọc phương trình vận tốc theo thời gian của vật
A - sai vì chuyển động thẳng đều có vận tốc không đổi
B - sai vì: \(a = 3,{v_0} = 0\) => vật chuyển động nhanh dần
C - sai vì \(a = - 2;{v_0} = 9\) => vật chuyển động chậm dần
D- đúng
Đặc điểm nào sau đây sai với chuyển động thẳng nhanh dần đều?
-
A.
Hiệu quãng đường đi được trong những khoảng thời gian liên tiếp luôn là hằng số.
-
B.
Vận tốc của vật luôn dương.
-
C.
Quãng đường đi biến đổi theo hàm bậc hai của thời gian.
-
D.
Vận tốc biến đổi theo hàm số bậc nhất của thời gian.
Đáp án : B
A, C, D - đúng
B - sai vì: Vận tốc của vật âm hay dương phụ thuộc vào chiều chuyển động của vật so với chiều dương của trục tọa độ mà ta chọn.
Chọn đáp án sai? Chất điểm chuyển động thẳng theo một chiều với gia tốc \(a = 4m/{s^2}\) có nghĩa là:
-
A.
Lúc đầu vận tốc bằng $0$ thì sau $1s$ sau vận tốc của nó bằng $4 m/s$.
-
B.
Lúc đầu vận tốc bằng $2 m/s$ thì sau $1 s$ sau vận tốc của nó bằng $6 m/s$.
-
C.
Lúc đầu vận tốc bằng $2 m/s$ thì sau $2 s$ sau vận tốc của nó bằng $8 m/s$.
-
D.
Lúc đầu vận tốc bằng $4 m/s$ thì sau $2 s$ sau vận tốc của nó bằng $12 m/s$.
Đáp án : C
Vận dụng biểu thức phương trình vận tốc: \(v = {v_0} + at\)
Ta có: Vận tốc được xác định bằng biểu thức \(v = {v_0} + at\)
A, B, D - đúng
C -sai vì: \(v = {v_0} + at \to v = 2 + 4.2 = 10m/s\left( {{v_0} = 2,t = 2} \right)\)
Phương trình chuyển động của một vật trên một đường thẳng có dạng \(x = 2{t^2} + 10t + 100(m;s)\).Thông tin nào sau đây là đúng?
-
A.
Vật chuyển động nhanh dần đều với gia tốc a = 2 m/s 2
-
B.
Vật chuyển động chậm dần đều với gia tốc a = 4 m/s 2
-
C.
Tọa độ của vật lúc t = 0 là 100 m
-
D.
Vận tốc của vật tại thời điểm t là v = 10 m/s
Đáp án : C
Đọc phương trình chuyển động thẳng biến đổi đều: \(x = {x_0} + {v_0}t + \frac{1}{2}a{t^2}\)
Từ phương trình chuyển động ta có: \(\left\{ \begin{array}{l}{x_0} = 100m\\{v_0} = 10m/s\\a = 4m/{s^2}\end{array} \right.\)
=> Vật chuyển động nhanh dần đều với gia tốc \(a = 4{\rm{ }}m/{s^2}\)
Tọa độ lúc ban đầu của vật là \({x_0} = 100m\)
Vận tốc của vật tại thời điểm ban đầu: \({v_0} = 10m/s\)
Phương trình chuyển động của một vật trên một đường thẳng có dạng \(x = 4{t^2} - 3t + 7(m;s)\). Điều nào sau đây là sai ?
-
A.
Gia tốc $a = 4m/{s^2}$
-
B.
Tọa độ ban đầu \({x_0} = 7m\)
-
C.
Gia tốc $a = 8m/{s^2}$
-
D.
Vận tốc ban đầu ${v_0} = - 3m/s$
Đáp án : A
Đọc phương trình chuyển động thẳng biến đổi đều: \(x = {x_0} + {v_0}t + \frac{1}{2}a{t^2}\)
Ta có: Gia tốc của vật là: a = 8m/s 2
=> A - sai
Đồ thị tọa độ theo thời gian của chất điểm chuyển động thẳng biến đổi đều có dạng
-
A.
Là đường thẳng song song với trục Ot
-
B.
Là đường thẳng có thể đi qua gốc tọa độ
-
C.
Là một nhánh parabol
-
D.
Là đường thẳng song song với trục Ox
Đáp án : C
Ta có phương trình tọa độ theo thời gian của chất điểm trong chuyển đông thẳng biến đổi đều có dạng: \(x = {x_0} + {v_0}t + \dfrac{1}{2}a{t^2}\)
=> Đồ thị của tọa độ theo thời gian của chất điểm chuyển động thẳng biến đổi đều là một nhánh parabol (dạng đồ thị giống hàm \(y = ax^2+bx+c\) nhưng ở đây ta có t>0 lên đồ thị chỉ là một nhánh parabol)
Đồ thị v - t nào sau đây là đồ thị trong đó a > 0
-
A.

-
B.

-
C.

-
D.

Đáp án : A
Đồ thị v - t trong đó a > 0 là đồ thị A
Đồ thị a - t của chuyển động thẳng biến đổi đều có dạng:
-
A.
Là đường thẳng song song với trục Ot
-
B.
Là đường thẳng có thể đi qua gốc tọa độ
-
C.
Là một nhánh parabol
-
D.
Là đường thẳng song song với trục Ox
Đáp án : A
Đồ thị a - t của chất điểm chuyển động thẳng biến đổi đều có dạng là đường thẳng song song với trục Ot
Một đoàn tàu bắt đầu rời ga. Chuyển động nhanh dần đều, sau $20s$ đạt đến vận tốc $36km/h$ . Hỏi sau bao lâu nữa tàu đạt được vận tốc $54km/h$?
-
A.
$t = 30s$
-
B.
$t = 5s$
-
C.
$t = 10s$
-
D.
$t = 20s$
Đáp án : C
Vận dụng biểu thức xác định gia tốc: \(a = \frac{{\Delta v}}{{\Delta t}}\)
Ta có: \(36km/h = 10m/s\)
+ Gia tốc của chuyển động: \(a = \frac{{10 - 0}}{{20}} = 0,5m/{s^2}\)
+ Phương trình vận tốc của vật: \(v = at = 0,5t\)
Thời gian để tàu đạt vận tốc \(54{\rm{ }}km/h = 15m/s\) tính từ lúc tàu đạt tốc độ 36km/h là: \(\Delta t = \frac{{15}}{{0,5}} - 20 = 30 - 20 = 10{\rm{s}}\)
Một vật chuyển động thẳng có phương trình \(x = 30 + 4t - {t^2}(m;s)\) . Tính quãng đường vật đi từ thời điểm $t_1 = 1s$ đến thời điểm $t_2 = 3s$?
-
A.
$2m$
-
B.
$0$
-
C.
$4m$
-
D.
Một đáp án khác
Đáp án : A
+ Xác định xem trong khoảng thời gian \(\Delta t\) vật có đổi chiều không
+ Thay t vào phương trình chuyển động để xác định quãng đường
Từ phương trình tọa độ - thời gian ta thu được phương trình vận tốc \(v = 4 - 2t \to v = 0 \leftrightarrow t = 2{\rm{s}}\) , vật sẽ đổi chiều chuyển động sau $2s$.
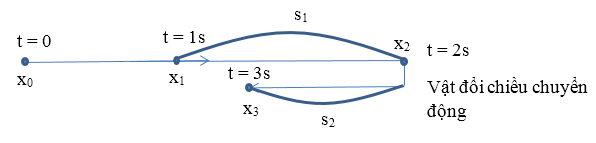
Do vậy quãng đường đi được của vật được tính:
\(s = {s_1} + {s_2} = \left| {{x_2} - {x_1}} \right| + \left| {{x_3} - {x_2}} \right| = \left| {4 - 3} \right| + \left| {3 - 4} \right| = 2m\)
Một vật đang chuyển động với vận tốc $36km/h$ , tài xế tắt máy và hãm phanh xe chuyển động chậm dần đều sau $50m$ nữa thì dừng lại. Quãng đường xe đi được trong $4s$ kể từ lúc bắt đầu hãm phanh là:
-
A.
20m
-
B.
32m
-
C.
18m
-
D.
2,5m
Đáp án : B
+ Vận dụng biểu thức độc lập: \({v^2} - v_0^2 = 2{\rm{as}}\)
+ Thay t vào phương trình chuyển động
Gia tốc của chuyển động: \(a = \frac{{{0^2} - {{10}^2}}}{{2.50}} = - 1m/{s^2}\) Quãng đường mà xe đi được trong 4 s kể từ lúc hãm phanh là: \(s = {v_0}t + \frac{1}{2}a{t^2} = 10.4 + \frac{1}{2}( - 1){.4^2} = 32m\)
Một vật chuyển động thẳng có phương trình vận tốc \(v = 2 - 2t\).Tốc độ trung bình của vật sau $4s$ kể từ lúc bắt đầu chuyển động là:
-
A.
-2m/s
-
B.
12m/s
-
C.
-12m/s
-
D.
2,5m/s
Đáp án : D
+ Xác định quãng đường đi của vật
+ Vận dụng biểu thức tính tốc độ trung bình: \({v_{tb}} = \frac{s}{t}\)
Ta để ý rằng sau $1s$ vật đã đổi chiều chuyển động
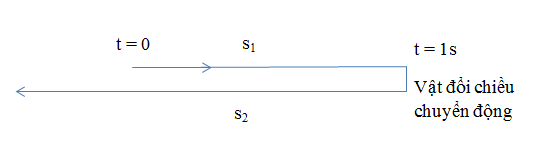
Chọn gốc thời gian là vị trí vật bắt đầu chuyển động, ta có:
Phương trình li độ của vật: \(x = {v_0}t + \dfrac{1}{2}a{t^2} = 2t - {t^2}\)
+ Tại \(t = 0\): \({x_0} = 0\)
+ Tại \(t = 1s\): \({x_1} = 1m\)
+ Tại \(t = 4s\): \({x_4} = - 8m\)
=> Ta suy ra:
+ Quãng đường vật đi được trong giây thứ nhất là: \({s_1} = {x_1} - {x_0} = 1m\)
+ Quãng đường vật đi được từ giây thứ 1 đến giây thứ 4 là: \({s_2} = \left| {{x_4} - {x_1}} \right| = \left| { - 8 - 1} \right| = 9m\)
=> Quãng đường vật đi được sau 4 s: \(s = {s_1} + {s_2} = 1 + 9 = 10m\) Tốc độ trung bình \({v_{tb}} = \dfrac{s}{t} = \dfrac{{10}}{{1 + 3}} = 2,5m/s\)
Một vật chuyển động thẳng nhanh dần đều, trong giây thứ hai vật đi được quãng đường dài $1,5m$. Tính quãng đường vật đi được trong giây thứ $100$?
-
A.
$199m$
-
B.
$200m$
-
C.
$99,5m$
-
D.
$210,5m$
Đáp án : C
Gọi a là gia tốc của chuyển động + Vận tốc của vật sau giây thứ nhất là \({v_{01}} = a.1 = a\) Quãng đường mà vật đi được trong giây thứ hai: \({s_2} = {v_{01}}t + \dfrac{1}{2}a{t^2} = a + \dfrac{a}{2} = 1,5{\rm{a = 1,5}} \to {\rm{a = 1m/}}{{\rm{s}}^2}\)
+ Vận tốc của vật sau giây thứ 99: \({v_{099}} = a.99 = 99m/s\)
Quãng đường vật đi được trong giây thứ 100: \({s_{100}} = {v_{099}}t + \dfrac{1}{2}a{t^2} = 99.1 + \dfrac{1}{2}1.1 = 99,5m\)
Phương trình nào sau đây cho biết vật chuyển động nhanh dần đều dọc theo chiều dương của trục x?
-
A.
\(x = 10 - 5t - 0,5{t^2}\)
-
B.
\(x = 10 - 5t + 0,5{t^2}\)
-
C.
\(x = 10 + 5t + 0,5{t^2}\)
-
D.
\(x = 10 + 5t - 0,5{t^2}\)
Đáp án : C
+ Đọc phương trình chuyển động của vật chuyển động nhanh dần đều
+ Sử dụng lí thuyết về chuyển động thẳng biến đổi đều
Chuyển động nhanh dần đều thì a và v cùng dấu, theo chiều dương của Ox nên a và v phải dương => Phương án C phù hợp với yêu cầu của đề bài
Vật chuyển động thẳng có phương trình \(x = 2{t^2} - 4t + 10(m;s)\) . Vật sẽ dừng lại tại vị trí :
-
A.
x = 10m
-
B.
x = 4m
-
C.
x = 6m
-
D.
x = 8m
Đáp án : D
+ Vật dừng lại khi có vận tốc bằng 0 - Giải phương trình v = 0 để tìm thời gian t
+ Thay t vào phương trình chuyển động => vị trí dừng lại
Phương trình vận tốc của vật:
\(\begin{array}{l}v = - 4 + 4t\\v = 0 \leftrightarrow - 4 + 4t = 0 \to t = 1{\rm{s}}\end{array}\)
Vật sẽ dừng lại tại vị trí \(x = {2.1^2} - 4.1 + 10 = 8m\)
Phương trình chuyển động của một vật có dạng \(x = 3 - 4t + 2{t^2}(m;s)\). Biểu thức vận tốc tức thời của vật theo thời gian là:
-
A.
\(v = 2(t - 2)m/s\)
-
B.
\(v = 4(t - 1)m/s\)
-
C.
\(v = 2(t - 1)m/s\)
-
D.
\(v = 2(t + 2)m/s\)
Đáp án : B
+ Đọc phương trình chuyển động
+ Viết phương trình vận tốc
Từ phương trình chuyển động ta có:
\(\left\{ \begin{array}{l}{v_0} = - 4\\a = 2.2 = 4m/{s^2}\end{array} \right.\)
=> Phương trình vận tốc: \(v = - 4 + 4t\)
Một vật chuyển động nhanh dần đều với vận tốc ban đầu $v_0 = 0$. Trong giây thứ nhất vật đi được quãng đường $s_1 = 3m$. Trong giây thứ hai vật đi được quãng đường $s_2$ bằng:
-
A.
$3m$
-
B.
$36m$
-
C.
$12m$
-
D.
Một đáp án khác.
Đáp án : D
+ Viết phương trình chuyển động của vật
+ Thay t vào phương trình chuyển động của vật
Chọn gốc tọa độ tại vị trí vật bắt đầu chuyển động
Gốc thời gian là lúc vật bắt đầu chuyển động
Ta có:
+ Phương trình chuyển động của vật là: $s = \dfrac{1}{2}a{t^2}$
+ Quãng đường vật đi được trong giây thứ nhất: \({s_1} = \dfrac{1}{2}a{.1^2} = 3 \to a = 6m/{s^2}\)
+ Quãng đường vật đi được trong hai giây đầu là \({s_2} = \dfrac{1}{2}{6.2^2} = 12m\)
=> Quãng đường vật đi được trong giây thứ 2 là: \(s = {s_2} - {s_1} = 12 - 3 = 9m\).
Một ôtô đang chuyển động với vận tốc $54km/h$ thì hãm phanh, chuyển động chậm dần đều và dừng lại sau $10s$. Chọn chiều dương là chiều chuyển động của ôtô .Vận tốc của ôtô sau khi hãm phanh được $6s$ là:
-
A.
2,5m/s
-
B.
6m/s
-
C.
7,5m/s
-
D.
9m/s.
Đáp án : B
+ Vận dụng biểu thức xác định gia tốc của chuyển động: \(a = \frac{{\Delta v}}{{\Delta t}}\)
+ Viết phương trình vận tốc
+ Thay t vào phương trình vận tốc
Đổi \(54km/h = 15m/s\)
Gia tốc của xe:
\(a = \frac{{0 - 15}}{{10}} = - 1,5m/{s^2}\)
Phương trình vận tốc của vật: \(v = 15 - 1,5t\)
Vận tốc của xe sau khi hãm phanh 6 s là: \(v = 15 - 1,5.6 = 6m/s\)
Một chiếc xe hơi giảm tốc chậm dần đều từ $54km/h$ còn $36km/h$ trên quãng đường thẳng dài $125m$. Vậy gia tốc của xe trên đoạn đường này là:
-
A.
-1,480m/s 2
-
B.
-0,072m/s 2
-
C.
-0,500m/s 2
-
D.
-1,000m/s 2
Đáp án : C
Vận dụng biểu thức độc lập: \({v^2} - v_0^2 = 2{\rm{as}}\)
Đổi \(54km/h = 15m/s,\,36km/h = 10m/s\)
Ta có: \({v^2} - v_0^2 = 2{\rm{as}} \to {\rm{a = }}\frac{{{v^2} - v_0^2}}{{2{\rm{s}}}} = \frac{{{{10}^2} - {{15}^2}}}{{2.125}} = - 0,5m/{s^2}\)
Một xe ôtô chuyển động chậm dần đều với vận tốc ban đầu \(v_0= 20m/s\) và gia tốc \(3m/s^2\). Vận tốc của xe khi đi thêm \(50m\) và quãng đường đi được cho đến khi dừng lại hẳn lần lượt có giá trị là:
-
A.
12,37m/s; 150m
-
B.
10m/s; 66,7m
-
C.
13,72m/s; 150m.
-
D.
13,27m/s; 200m .
Đáp án : B
Vận dụng biểu thức độc lập: \({v^2} - v_0^2 = 2{\rm{as}}\)
Ta có: \({v^2} - v_0^2 = 2{\rm{as}}\)
Vận tốc của xe khi đi được quãng đường \(50 m\): \({v_1}^2 - v_0^2 = 2{\rm{a}}{{\rm{s}}_1} \to v = \sqrt {2{\rm{a}}{{\rm{s}}_1} + v_0^2} = \sqrt {2.( - 3).50 + {{20}^2}} = 10m/s\) Quãng đường vật đi được cho đến khi dừng hẳn: \({v^2} - v_0^2 = 2{\rm{as}} \to s = \dfrac{{{v^2} - v_0^2}}{{2{\rm{a}}}} = \dfrac{{{0^2} - {{20}^2}}}{{2.( - 3)}} = 66,67m\)
Một đoàn tàu đang chạy với vận tốc 72km/h thì hãm phanh, chạy chậm dần đều sau 10s vận tốc giảm xuống còn 54km/h . Hỏi sau bao lâu thì tàu dừng lại hẳn
-
A.
Sau 55s từ lúc hãm phanh.
-
B.
Sau 50s từ lúc hãm phanh.
-
C.
Sau 45s từ lúc hãm phanh
-
D.
Sau 40s từ lúc hãm phanh
Đáp án : D
+ Vận dụng biểu thức xác định gia tốc của chuyển động: \(a = \frac{{\Delta v}}{{\Delta t}}\)
+ Viết phương trình vận tốc
+ Thay t vào phương trình vận tốc
Gia tốc của xe : \(a = \frac{{15 - 20}}{{10}} = - 0,5m/{s^2}\)
Phương trình vận tốc của vật: \(v = 20 - 0,5t\)
Xe dừng lại hẳn khi: \(v = 0 \leftrightarrow 20 - 0,5t = 0 \to t = 40{\rm{s}}\)
Lúc 7 h, hai ôtô bắt đầu khởi hành từ hai điểm A, B cách nhau 2400 m, chuyển động nhanh dần đều và ngược chiều nhau. ôtô đi từ A có gia tốc 1 m/s 2 , còn ôtô từ B có gia tốc 2 m/s 2 . Chọn chiều dương hướng từ A đến B, gốc thời gian lúc 7 h. Xác định vị trí hai xe gặp nhau:
-
A.
1600m
-
B.
1200m
-
C.
800m
-
D.
2400m
Đáp án : C
+ Viết phương trình chuyển động của 2 xe
+ Giải phương trình x 1 = x 2
+ Thay t vào phương trình của 1 xe
Ta có:
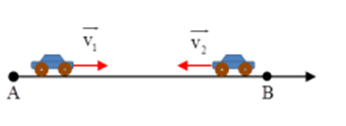
+ Phương trình chuyển động của hai ô tô lúc này là: \(\left\{ \begin{array}{l}A:{x_1} = \dfrac{1}{2}{t^2}\\B:{x_2} = 2400 - {t^2}\end{array} \right.\) + Khi hai xe gặp nhau: \({x_1} = {x_2} \leftrightarrow \dfrac{1}{2}{t^2} = 2400 - {t^2} \to t = 40{\rm{s}}\) Vậy vị trí hai xe gặp cách A một khoảng: \(x = {x_1}(t = 40{\rm{s}}) = \dfrac{1}{2}{.40^2} = 800m\)
Cùng một lúc tại hai điểm $A, B$ cách nhau $125 m$ có hai vật chuyển động ngược chiều nhau. Vật đi từ $A$ có vận tốc đầu $4 m/s$ và gia tốc là $2 m/{s^2}$, vật đi từ B có vận tốc đầu $6 m/s$ và gia tốc $4 m/{s^2}$. Biết các vật chuyển động nhanh dần đều. Chọn $A$ làm gốc tọa độ, chiều dương hướng từ $A$ đến $B$, gốc thời gian lúc hai vật cùng xuất phát. Xác định thời điểm hai vật gặp nhau?
-
A.
10s
-
B.
5s
-
C.
6s
-
D.
12s
Đáp án : B
+ Viết phương trình chuyển động của 2 xe
+ Giải phương trình x 1 = x 2
+ Thay t vào phương trình của 1 xe
Ta có:

+ Phương trình chuyển động của hai ô tô lúc này là: \(\left\{ \begin{array}{l}A:{x_1} = 4t + {t^2}\\B:{x_2} = 125 - 6t - 2{t^2}\end{array} \right.\) + Khi hai xe gặp nhau:
\(\begin{array}{l}{x_1} = {x_2} \leftrightarrow 4t + {t^2} = 125 - 6t - 2{t^2}\\ \leftrightarrow 3{t^2} + 10t - 125 = 0\\ \to \left[ \begin{array}{l}t = 5{\rm{s}}\\t = - \frac{{25}}{3}(L)\end{array} \right.\end{array}\) Vậy thời điểm $2$ xe gặp nhau là $5s$
Một xe ôtô đi từ Ba La vào trung tâm Hà Nội có đồ thị v-t như hình vẽ:

Quãng đường mà ôtô đi được là:
-
A.
$1km$
-
B.
$1,5km$
-
C.
$1,4km$
-
D.
$2km$
Đáp án : A
+ Đọc đồ thị v - t
+ Vận dụng biểu thức: \(s = v.t\)
Ta có:
+ Trên đoạn \(A \to B\) xe chuyển động chậm dần đều với gia tốc: \({a_1} = \frac{{{v_B} - {v_A}}}{{\Delta t}} = \frac{{10 - 20}}{{20}} = - 0,5m/{s^2}\)
Quãng đường vật đi được: \({s_1} = 20t - 0,25{t^2} = 20.20 - 0,{25.20^2} = 300m\)
+ Trên đoạn \(B \to C\) xe chuyển động thẳng đều với vận tốc \(v = 10m/s\)
Quãng đường vật đi được: \({s_2} = vt = 10.30 = 300m\)
+ Trên đoạn \(C \to D\) xe chuyển động chậm dần đều với gia tốc:
\({a_3} = \frac{{0 - 10}}{{130 - 50}} = - 0,125m/s{}^2\)
Quãng đường vật đi được: \({s_3} = 10t - 0,0625{t^2} = 10.80 - 0,{0625.80^2} = 400m\)
Vậy quãng đường mà ôtô đi được là: \(s = {s_1} + {s_2} + {s_3} = 300 + 300 + 400 = 1000m\)
Cho đồ thị v - t của hai ôtô như hình vẽ:

Giao điểm của đồ thị cho biết:
-
A.
Thời điểm 2 xe gặp nhau
-
B.
Thời điểm 2 xe có cùng tốc độ
-
C.
Khoảng cách 2 xe gặp nhau
-
D.
Cả A và B
Đáp án : B
Giao điểm của đồ thị cho biết thời điểm 2 xe có cùng tốc độ
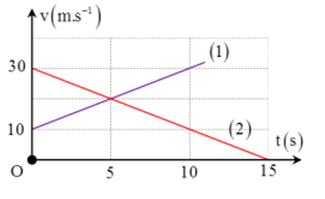
Cho đồ thị v - t của hai ôtô như hình vẽ:

Chọn phương án đúng ?
-
A.
\({v_1} = 10 - 2t\)
-
B.
\({v_2} = 30 - 2t\)
-
C.
\({v_2} = 30 + 2t\)
-
D.
\({v_2} = 10 - 1,5t\)
Đáp án : B
Từ đồ thị ta suy ra,
+ Phương trình vận tốc của oto 1 là: \({v_1} = 10 + 2t\)
+ phương trình vận tốc của oto 2 là: \({v_2} = 30 - 2t\)
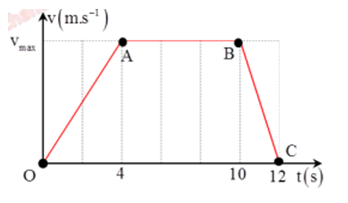
Một chất điểm chuyển động thẳng có đồ thị vận tốc - thời gian như hình vẽ. Trong suốt quá trình chuyển động, tốc độ trung bình là 9 m/s. Phương trình chuyển động của chất điểm khi đi từ B đến C là?

-
A.
\(x = 24 + 12(t - 4)\)
-
B.
\(x = 1,5{t^2}\)
-
C.
\(x = 96 + 12(t - 10) - 3{(t - 10)^2}\)
-
D.
\(x = 24 + 12t - 3{t^2}\)
Đáp án : C
+ Đọc đồ thị v - t
+ Vận dụng biểu thức: \(a = \dfrac{{\Delta v}}{{\Delta t}}\)
Ta có :
+ Tốc độ trung bình của vật : \({v_{tb}} = \dfrac{s}{t} = \dfrac{{\dfrac{1}{2}{v_{{\rm{max}}}}.4 + {v_{{\rm{max}}}}.6 + \dfrac{1}{2}{v_{{\rm{max}}}}.2}}{{12}} = 9 \to {v_{{\rm{max}}}} = 12m/s\)
+ Gia tốc của chất điểm khi chuyển động từ B đến C: \(a = \dfrac{{0 - 12}}{2} = - 6m/s\)
=> Phương trình chuyển động của chất điểm khi đi từ B đến C là: \(x = 96 + 12(t - 10) - 3{(t - 10)^2}\)
Ba vật chuyển động thẳng có đồ thị v - t như hình vẽ:

Sau bao nhiêu giây thì vật thứ 3 sẽ dừng lại?
-
A.
5s
-
B.
1s
-
C.
2s
-
D.
3s
Đáp án : D
Ta có vật dừng lại khi v = 0
Từ đồ thị, ta có: vật thứ 3 có vận tốc bằng không khi t = 3s
=> Sau 3s thì vật thứ 3 sẽ dừng lại
Một vật chuyển động thẳng chậm dần đều với tốc độ đầu \(3m/s\) và gia tốc \(2m/s^2,\) thời điểm ban đầu ở gốc toạ độ và chuyển động ngược chiều dương của trục toạ độ thì phương trình có dạng.
-
A.
\(x = 3t + t^2\)
-
B.
\(x = -3t - 2t^2\)
-
C.
\(x = -3t + t^2\)
-
D.
\(x = 3t - t^2\)
Đáp án : C
Phương trình chuyển động thẳng biến đổi đều: \(x = {x_0} + {v_0}t + \dfrac{1}{2}a{t^2}\)
Ta có: \(\left\{ \begin{array}{l}{x_0} = 0\\{v_0} = - 3m/s\\a = 2m/{s^2}\end{array} \right.\)
Phương trình chuyển động của vật: \(x = - 3t + {t^2}\,\,\left( m \right)\)
Phương trình của một vật chuyển động thẳng là : \(x = 6 + 12t + {t^2}{\mkern 1mu} {\mkern 1mu} \left( {cm;s} \right)\)
a) Xác định gia tốc và vận tốc ban đầu của vật?
b) Viết công thức vận tốc và tính vận tốc của vật sau \(2s\) kể từ thời điểm ban đầu.
-
A.
\(a)\,{v_0} = 12cm/s;a = 2cm/{s^2}\,\,\,b)\,16cm/s\)
-
B.
\(a)\,{v_0} = 6cm/s;a = 1cm/{s^2}\,\,\,b)\,6cm/s\)
-
C.
\(a)\,{v_0} = 6cm/s;a = 12cm/{s^2}\,\,\,b)\,30cm/s\)
-
D.
\(a)\,{v_0} = 12cm/s;a = 6cm/{s^2}\,\,\,b)\,24cm/s\)
Đáp án : A
Phương trình của một vật chuyển động thẳng biến đổi đều là :\(x = {x_0} + {v_0}.t + \dfrac{1}{2}.a.{t^2}\)
Công thức tính vận tốc: \(v = {v_0} + at\)
Với \(v_0\) là vận tốc đầu; \(a\) là gia tốc
Phương trình chuyển động: \(x = 6 + 12t + {t^2}{\mkern 1mu} {\mkern 1mu} \left( {cm;s} \right)\)
a) Vận tốc ban đầu và gia tốc:\(\left\{ {\begin{array}{*{20}{l}}{{v_0} = 12cm/s}\\{a = 2cm/{s^2}}\end{array}} \right.\)
b) Công thức vận tốc : \(v = 12 + 2t\)
Sau \(2\) giây thì vận tốc của vật là : \(v = 12 + 2.2 = 16cm/s\)
Một xe chuyển động nhanh dần đều đi được S = 24m, S 2 = 64m trong 2 khoảng thời gian liên tiếp bằng nhau là 4s. Xác định vận tốc ban đầu và gia tốc.
-
A.
\({v_{01}} = 1m/s,\;a = 2,5m/{s^2}\)
-
B.
\({v_{01}} = 1m/s,\;a = 2m/{s^2}\)
-
C.
\({v_{01}} = 1m/s,\;a = 3,5m/{s^2}\)
-
D.
\({v_{01}} = 1,5m/s,\;a = 2,5m/{s^2}\)
Đáp án : A
Áp dụng biểu thức tính vận tốc và quãng đường trong chuyển động thẳng biến đổi đều \(v = {v_0} + at;s = {v_0}t + \frac{1}{2}a{t^2}\)
Quãng đường vật đi được trong 2 khoảng thời gian liên tiếp bằng nhau là 4s là :
\(\begin{array}{l}{S_1}\; = {v_{01}}{t_1} + \frac{1}{2}a{t_1}^24.{v_{01}} + 8a = 24{\rm{ }}\left( 1 \right)\\{S_2} = {v_{02}}{t_2} + \frac{1}{2}a{t_2}^2\;4.{v_{01}} + 8a = 64{\rm{ }}\left( 2 \right)\end{array}\)
Mà \({v_{02}} = {v_1} = {v_{01}} + a{t_2}\left( 3 \right)\)
Giải (1), (2), (3) ta được : \({v_{01}} = 1m/s,\;a = 2,5m/{s^2}\)
Hai người đi xe đạp khởi hành cùng một lúc từ 2 địa điểm A và B, đi ngược chiều nhau. Người đi từ A có vận tốc đầu là \(18km/h\) và chuyển động chậm dần đều với gia tốc \(20cm/{s^2}\). Người đi từ B có vận tốc đầu là \(5,4m/s\) và chuyển động nhanh dần đều với gia tốc\(0,2m/{s^2}\). Khoảng cách giữa hai người lúc đầu là \(130m\). Hỏi sau bao lâu 2 người gặp nhau và vị trí gặp nhau?
-
A.
\(t = 12,5s\); cách A \(83,125m\)
-
B.
\(t = 20s\); cách B \(60m\)
-
C.
\(t = 20s\); cách A \(60m\)
-
D.
\(t = 12,5s\); cách A \(46,875m\)
Đáp án : D
Phương trình của chuyển động thẳng đều: \(x = {x_0} + {v_0}t + \dfrac{1}{2}a{t^2}\)
Hai vật gặp nhau khi: \({x_1} = {x_2} \Rightarrow t\)
Chọn gốc tọa độ tại A, chiều dương là chiều từ A đến B, gốc thời gian là lúc hai người bắt đầu khởi hành.
Xe xuất phát từ A có:
\(\left\{ \begin{array}{l}{x_A} = 18km/h = 5m/s\\{a_A} = - 20cm/{s^2} = - 0,2m/{s^2}\\{x_{0A}} = 0\end{array} \right. \Rightarrow {x_A} = 5t - 0,1{t^2}\,\left( m \right)\)
Xe xuất phát từ B có:
\(\left\{ \begin{array}{l}{x_B} = - 5,4m/s\\{a_B} = - 0,2m/{s^2}\\{x_{0B}} = 130m\end{array} \right. \Rightarrow {x_B} = 130 - 5,4t - 0,1{t^2}\,\left( m \right)\)
Hai xe gặp nhau khi:
\(\begin{array}{l}{x_A} = {x_B} \Leftrightarrow 5t - 0,1{t^2} = 130 - 5,4t - 0,1{t^2}\\ \Rightarrow t = 12,5s\end{array}\)
Thay \(t = 12,5s\) vào phương trình của \({x_A}\) ta được:
\({x_A} = 5.12,5 - 0,1.12,{5^2} = 46,875m\)
Một ô tô đang chuyển động với vận tốc 54km/h thì hãm phanh chuyển động chậm dần đều đi được 20m thì vận tốc còn 18km/h. Tính gia tốc của ô tô và quãng đường ô tô đi được từ lúc hãm phanh đến lúc dừng hẳn.
-
A.
\( - 5m/{s^2};\,\,22,5m\)
-
B.
\(5m/{s^2};\,\,22,5m\)
-
C.
\(3m/{s^2};\,\,30m\)
-
D.
\( - 3m/{s^2};\,\,30m\)
Đáp án : A
Công thức liên hệ giữa s,v và a: \({v^2} - v_0^2 = 2a.s\)
Ta có: \(\left\{ \begin{array}{l}{v_0} = 54km/h = 15m/s\\v = 18km/h = 5m/s\\s = 20m\end{array} \right.\)
Áp dụng công thức liên hệ giữa s, v, a ta có:
\({v^2} - v_0^2 = 2a.s \Rightarrow a = \dfrac{{{v^2} - v_0^2}}{{2s}} = \dfrac{{{5^2} - {{15}^2}}}{{2.20}} = - 5m/{s^2}\)
Khi ô tô dừng hẳn thì: \(v' = 0\)
Áp dụng công thức liên hệ giữa s’, v’, a ta có:
\(v{'^2} - {v^2} = 2a.s' \Rightarrow s' = \dfrac{{v{'^2} - {v^2}}}{{2a}} = \dfrac{{{0^2} - {{15}^2}}}{{2.\left( { - 5} \right)}} = 22,5m\)