Bài 1, 2, 3, 4 trang 170 SGK Toán 4
Bài 1: Phân số thứ nhất là ...
Bài 1
Phân số thứ nhất là \(\dfrac{4}{5}\), phân số thứ hai là \(\dfrac{2}{7}\). Hãy tính tổng, hiệu, tích, thương của phân số thứ nhất và phân số thứ hai.
Phương pháp giải:
- Muốn cộng (hoặc trừ) hai phân số khác mẫu số ta quy đồng mẫu số hai phân số rồi cộng (hoặc trừ) hai phân số đã quy đồng mẫu số.
- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
- Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Lời giải chi tiết:
Tính tổng: \(\dfrac{4}{5}+\dfrac{2}{7}=\dfrac{28}{35}+\dfrac{10}{35}= \dfrac{38}{35}\)
Tính hiệu: \(\dfrac{4}{5}-\dfrac{2}{7}= \dfrac{28}{35}- \dfrac{10}{35}= \dfrac{18}{35}\)
Tính tích: \(\dfrac{4}{5}\times \dfrac{2}{7}=\dfrac{8}{35}\)
Tính thương: \(\dfrac{4}{5}: \dfrac{2}{7}=\dfrac{4}{5}\times \dfrac{7}{2}\) \(= \dfrac{28}{10}= \dfrac{14}{5}\)
Bài 2
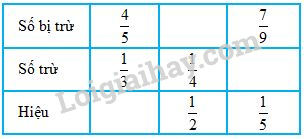
Số ?
a)
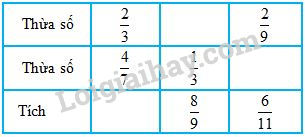
b)
Phương pháp giải:
Áp dụng các công thức:
a) Số bị trừ \(=\) Hiệu \(+\) Số trừ ;
Số trừ \(=\) Số bị trừ \(-\) Hiệu ;
Hiệu \(=\) Số bị trừ \(-\) Số trừ.
b) Tích \(=\) Thừa số \(\times\) Thừa số ;
Thừa số \(=\) Tích \(:\) Thừa số đã biết.
Lời giải chi tiết:
a) Cột thứ nhất: \(\dfrac{4}{5}-\dfrac{1}{3}=\dfrac{12}{15}-\dfrac{5}{15}\)\(=\dfrac{7}{15}\), viết \(\dfrac{7}{15}\) vào ô trống.
Cột thứ hai: \(\dfrac{1}{2}+ \dfrac{1}{4}=\dfrac{4}{8}+ \dfrac{2}{8}\) \(=\dfrac{6}{8}= \dfrac{3}{4}\), viết \(\dfrac{3}{4}\) vào ô trống.
Cột thứ ba: \(\dfrac{7}{9}-\dfrac{1}{5}=\dfrac{35}{45}-\dfrac{9}{45}=\dfrac{26}{45}\), viết \(\dfrac{26}{45}\) vào ô trống.
Ta có kết quả như sau:
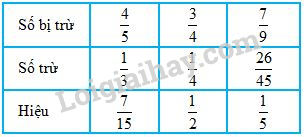
b) Cột thứ nhất: \(\dfrac{2}{3}\times \dfrac{4}{7}= \dfrac{8}{21}\), viết \(\dfrac{8}{21}\) vào ô trống.
Cột thứ hai: \(\dfrac{8}{9}: \dfrac{1}{3}=\dfrac{8}{9}\times \dfrac{3}{1}= \dfrac{24}{9}=\dfrac{8}{3}\), viết \(\dfrac{8}{3}\) vào ô trống.
Cột thứ ba: \(\dfrac{6}{11}:\dfrac{2}{9}=\dfrac{6}{11}\times \dfrac{9}{2}= \dfrac{54}{22}= \dfrac{27}{11}\), viết \(\dfrac{27}{11}\) vào ô trống.
Ta có kết quả như sau:
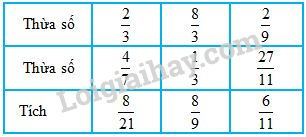
Bài 3
Tính:
a) \(\dfrac{2}{3}+ \dfrac{5}{2}-\dfrac{3}{4}\) ; \(\dfrac{2}{5}\times \dfrac{1}{2}: \dfrac{1}{3}\); \(\dfrac{2}{9}: \dfrac{2}{9}\times \dfrac{1}{2}\) .
b) \(\dfrac{4}{5}-\dfrac{1}{2}+ \dfrac{1}{3}\) ; \(\dfrac{1}{2}\times \dfrac{1}{3}+ \dfrac{1}{4}\) ; \(\dfrac{2}{7}: \dfrac{2}{3}- \dfrac{1}{7}\)
Phương pháp giải:
- Biểu thức chỉ có phép cộng và phép trừ hoặc chỉ có phép nhân và phép chia thì ta tính lần lượt từ trái sang phải.
- Biểu thức có các phép cộng, phép trừ , phép nhân, phép chia thì ta thực hiện tính phép nhân, phép chia trước, thực hiện tính phép cộng, trừ sau.
Lời giải chi tiết:
a) \(\dfrac{2}{3}+ \dfrac{5}{2}-\dfrac{3}{4}=\dfrac{8}{12}+ \dfrac{30}{12}- \dfrac{9}{12}\)\(=\dfrac{38}{12}- \dfrac{9}{12}= \dfrac{29}{12}\)
+) \(\dfrac{2}{5}\times \dfrac{1}{2}: \dfrac{1}{3}\) \(=\dfrac{2}{10}: \dfrac{1}{3}\)\(=\dfrac{1}{5}: \dfrac{1}{3}\) \(= \dfrac{1}{5}\times \dfrac{3}{1}= \dfrac{3}{5}\)
+) \(\dfrac{2}{9}: \dfrac{2}{9}\times \dfrac{1}{2}= \dfrac{2}{9}\times \dfrac{9}{2} \times \dfrac{1}{2}\)\(= \dfrac{18}{18} \times \dfrac{1}{2} = 1 \times \dfrac{1}{2} = \dfrac{1}{2}\)
b) \(\dfrac{4}{5}-\dfrac{1}{2}+ \dfrac{1}{3}= \dfrac{24}{30}- \dfrac{15}{30}+ \dfrac{10}{30}\)\(= \dfrac{9}{30}+ \dfrac{10}{30}= \dfrac{19}{30}\)
+) \(\dfrac{1}{2}\times \dfrac{1}{3}+ \dfrac{1}{4}= \dfrac{1}{6}+ \dfrac{1}{4}\)\(= \dfrac{2}{12}+ \dfrac{3}{12}= \dfrac{5}{12}\)
+) \(\dfrac{2}{7}: \dfrac{2}{3} - \dfrac{1}{7}= \dfrac{2}{7}\times \dfrac{3}{2}- \dfrac{1}{7}\)\(=\dfrac{6}{14}- \dfrac{1}{7} = \dfrac{3}{7}- \dfrac{1}{7}=\dfrac{2}{7}\)
Bài 4
Người ta cho một vòi nước chảy vào bể chưa có nước, giờ thứ nhất chảy được \(\dfrac{2}{5}\) bể, giờ thứ hai chảy được \(\dfrac{2}{5}\) bể.
a) Hỏi sau \(2\) giờ vòi nước đó chảy vào được mấy phần bể ?
b) Nếu đã dùng hết một lượng nước bằng \(\dfrac{1}{2}\) bể thì số nước còn lại là mấy phần bể ?
Phương pháp giải:
- Số nước chảy vào bể sau \(2\) giờ = số nước chảy vào bể giờ thứ nhất \(+\) số nước chảy vào bể giờ thứ hai.
- Số nước còn lại = số nước ban đầu có trong bể \(-\) số nước đã dùng.
Lời giải chi tiết:
Tóm tắt
Giờ thứ nhất: \(\dfrac{2}{5}\) bể
Giờ thứ hai:\(\dfrac{2}{5}\) bể
a) Sau 2 giờ: .... bể?
b) Đã dùng: \(\dfrac{1}{2}\) bể
Còn lại: ... bể?
Bài giải
a) Sau hai giờ vòi nước chảy được số phần bể là:
\(\dfrac{2}{5}+\dfrac{2}{5}= \dfrac{4}{5}\) (bể)
b) Số phần nước còn lại sau khi dùng \(\dfrac{1}{2}\) bể là:
\(\dfrac{4}{5}-\dfrac{1}{2}= \dfrac{3}{10}\) (bể)
Đáp số: a) \(\dfrac{4}{5}\) bể;
b) \(\dfrac{3}{10}\) bể.