Bài 1, 2, 3 trang 119 SGK Toán 4 — Không quảng cáo

Bài 1

So sánh hai phân số:

$\dfrac{3}{7}$ và $\dfrac{5}{7}$                                b) $\dfrac{4}{3}$ và $\dfrac{2}{3}$

c) $\dfrac{7}{8}$ và $\dfrac{5}{8}$                           d) $\dfrac{2}{11}$ và $\dfrac{9}{11}$

Phương pháp giải:

Trong hai phân số cùng mẫu số:

- Phân số nào có tử số bé hơn thì bé hơn.

- Phân số nào có tử số lớn hơn thì lớn hơn.

- Nếu tử số bằng nhau thì hai phân số đó bằng nhau.

Lời giải chi tiết:

a) $\dfrac{3}{7} <  \dfrac{5}{7}$                            b) $\dfrac{4}{3} > \dfrac{2}{3}$

c) $\dfrac{7}{8}> \dfrac{5}{8}$                            d) $\dfrac{2}{11}< \dfrac{9}{11}$

Bài 2

a) Nhận xét:

$\dfrac{2}{5}< \dfrac{5}{5}$ mà $\dfrac{5}{5} = 1$ nên $\dfrac{2}{5} < 1$.

Nếu tử số bé hơn mẫu số thì phân số bé hơn $1$.

$\dfrac{8}{5} > \dfrac{5}{5}$ mà $\dfrac{5}{5} = 1$  nên $\dfrac{8}{5} > 1$.

b) So sánh các phân số sau với $1$:

$\dfrac{1}{2}$ ;   $\dfrac{4}{5}$ ;    $\dfrac{7}{3}$;    $\dfrac{6}{5}$ ;    $\dfrac{9}{9}$;    $\dfrac{12}{7}$

Phương pháp giải:

- Phân số có tử số bé hơn mẫu số thì phân số bé hơn $1$.

- Phân số có tử số lớn hơn mẫu số thì phân số lớn hơn $1$.

- Phân số có tử số bằng mẫu số thì phân số bằng $1$.

Lời giải chi tiết:

$\dfrac{1}{2} < 1$  ;                         $\dfrac{4}{5} < 1$  ;                           $\dfrac{7}{3} > 1$ ;

$\dfrac{6}{5} > 1$;                           $\dfrac{9}{9} = 1$  ;                          $\dfrac{12}{7} > 1$.

Bài 3

Viết các phân số bé hơn $1$, có mẫu số là $5$ và tử số khác $0$.

Phương pháp giải:

Phân số có tử số bé hơn mẫu số thì phân số bé hơn 1.

Lời giải chi tiết:

Các phân số bé hơn $1$, có mẫu số là $5$ và tử số khác $0$ là :

$\dfrac{1}{5}; \quad \dfrac{2}{5}; \quad \dfrac{3}{5}; \quad \dfrac{4}{5}$.

Lý thuyết

Ví dụ : So sánh hai phân số $\dfrac{2}{5}$ và $\dfrac{3}{5}$.

Vẽ đoạn thẳng AB. Chia đoạn thẳng AB thành 5 phần bằng nhau. Độ dài đoạn thẳng AC bằng $\dfrac{2}{5}$ độ dài đoạn thẳng AB. Độ dài đoạn thẳng AD bằng $\dfrac{3}{5}$ độ dài đoạn thẳng AB.

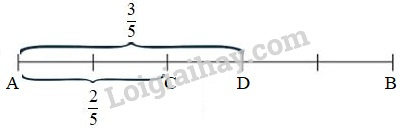
Nhìn hình vẽ ta thấy :

$\dfrac{2}{5} <\dfrac{3}{5}$       ;       $\dfrac{3}{5} >\dfrac{2}{5}$

Trong hai phân số cùng mẫu số :

• Phân số nào có tử số bé hơn thì bé hơn.

• Phân số nào có tử số lớn hơn thì lớn hơn.

• Nếu tử số bằng nhau thì hai phân số đó bằng nhau.