Bài 1 trang 81 SGK Toán 11 tập 2 – Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho hình chóp $S.ABCD$, đáy $ABCD$ là hình thoi cạnh $a$ có $O$ là giao điểm của hai đường chéo, $\widehat {ABC} = {60^ \circ },SO \bot \left( {ABCD} \right),SO = a\sqrt 3$. Tính khoảng cách từ $O$ đến mặt phẳng $\left( {SCD} \right)$.

Lời giải chi tiết

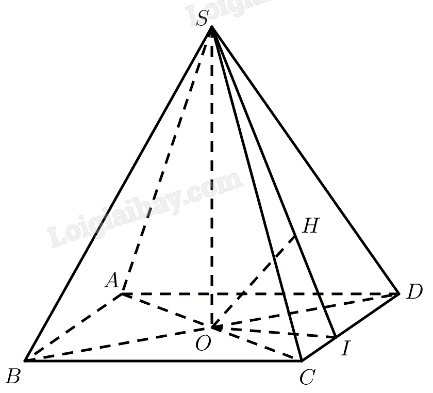
Kẻ $OI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right),OH \bot SI\left( {H \in SI} \right)$.

Ta có:

$\begin{array}{l}\left. \begin{array}{l}SO \bot \left( {ABCD} \right) \Rightarrow SO \bot C{\rm{D}}\\OI \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SOI} \right)\\\left. \begin{array}{l} \Rightarrow C{\rm{D}} \bot OH\\OH \bot SI\end{array} \right\} \Rightarrow OH \bot \left( {SC{\rm{D}}} \right)\\ \Rightarrow d\left( {O,\left( {SC{\rm{D}}} \right)} \right) = OH\end{array}$

$\Delta ABC$ đều $\Rightarrow AC = a \Rightarrow OC = \frac{1}{2}AC = \frac{a}{2}$

$\Delta ABD$ có $\widehat {BA{\rm{D}}} = {120^ \circ } \Rightarrow B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2} - 2{\rm{A}}B.A{\rm{D}}}  = a\sqrt 3  \Rightarrow OD = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 3 }}{2}$

$\Delta OCD$ vuông tại $O$ có đường cao $OI$

$\Rightarrow OI = \frac{{OC.O{\rm{D}}}}{{C{\rm{D}}}} = \frac{{a\sqrt 3 }}{4}$

$SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI \Rightarrow \Delta SOI$ vuông tại $O$ có đường cao $OH$

$\Rightarrow OH = \frac{{SO.OI}}{{\sqrt {S{O^2} + O{I^2}} }} = \frac{{a\sqrt {51} }}{{17}}$

Vậy $d\left( {O,\left( {SCD} \right)} \right) = OH = \frac{{a\sqrt {51} }}{{17}}$.