Bài 14 trang 42 SGK Toán 11 tập 1 - Chân trời sáng tạo
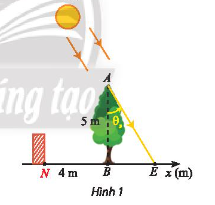
Trong Hình 1, cây xanh AB nằm trên đường xích đạo được trồng vuông góc với mặt đất và có chiều cao 5 m.
Đề bài
Trong Hình 1, cây xanh AB nằm trên đường xích đạo được trồng vuông góc với mặt đất và có chiều cao 5 m. Bóng của cây là BE. Vào ngày xuân phân và hạ phân, điểm E di chuyển trên đường thẳng Bx. Góc thiên đỉnh \({\theta _t} = (AB,AE)\) phụ thuộc vào vị trí của Mặt trời và thay đổi theo thời gian trong ngày theo công thức \({\theta _s}(t) = (AB,AE) = \frac{\pi }{{12}}(t - 12)\;\) rad với t là thời gian trong ngày (theo đơn vị giờ, 6 < t < 18).
(Theo https://www.sciencedirect.com/topics/engineering/solar-hour-angle)
a) Viết hàm số biểu diễn toạ độ của điểm E trên trục Bx theo t.
b) Dựa vào đồ thị hàm số tang, hãy xác định các thời điểm mà tại đó bóng cây phủ qua vị trí tường rào N biết N nằm trên trục Bx với toạ độ là \({x_N} = - 4\;\) (m). Làm tròn kết quả đến hàng phần mười.
Phương pháp giải - Xem chi tiết
a, Dựa vào hình vẽ để viết hàm số biểu diễn tọa độ điểm E.
b, Giải bất phương trình để tìm ra t.
Lời giải chi tiết
a) Xét tam giác ABE vuông tại B, có:
\(tan{\theta _s}(t) = \frac{{BE}}{{AB}} \Leftrightarrow BE = 5tan\left( {\frac{\pi }{{12}}(t - 12)} \right)\)
b) Đồ thị của hàm số \({\theta _s} = 5tan\left( {\frac{\pi }{{12}}(t - 12)} \right)\)
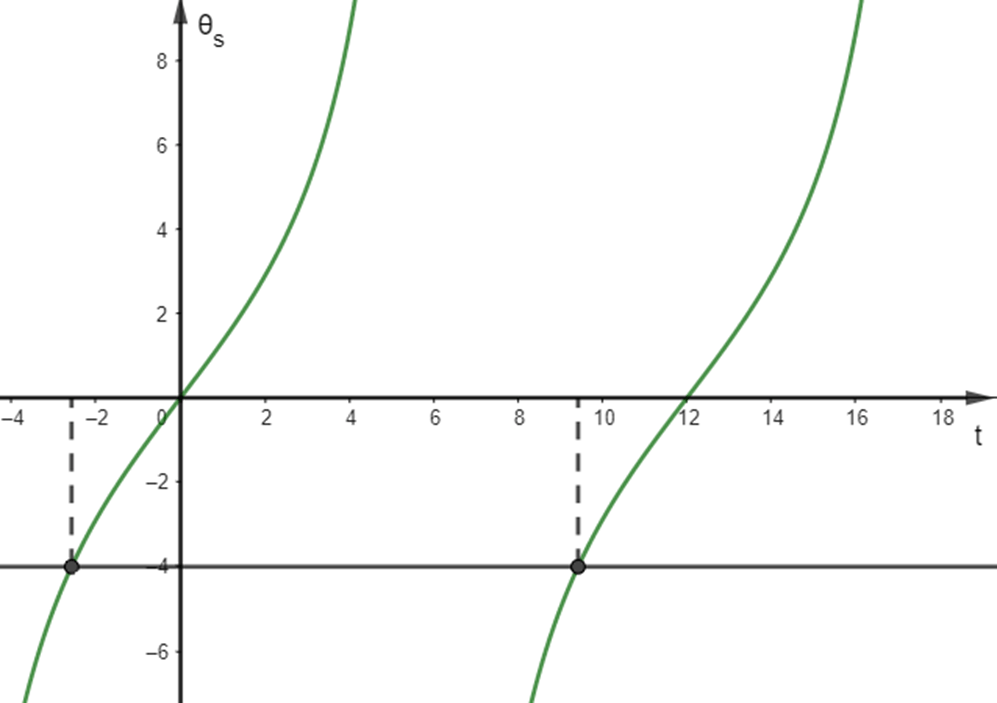
Dựa vào đồ thị hàm số để \({\theta _s} = 5tan\left( {\frac{\pi }{{12}}(t - 12)} \right) < - 4\)
\(\begin{array}{l} \Leftrightarrow tan\left( {\frac{\pi }{{12}}(t - 12)} \right) < - \frac{4}{5}\\ \Leftrightarrow \frac{\pi }{{12}}(t - 12) < - 0,67\\ \Leftrightarrow t < 9,4\end{array}\)
Kết hợp điều kiện \(6 < t < 18 \Rightarrow 6 < t < 9,4\).
Vậy thời điểm bóng cây phủ qua hàng rào là 6 < t < 9,4.