Bài 18 trang 170 Tài liệu dạy – học Toán 7 tập 1
Giải bài tập Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
Đề bài
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a) Kẻ \(HF \bot AB,HF \bot AC(E \in AB,F \in AC).\) Chứng minh rằng AE = AF.
b) Chứng minh rằng EF // BC.
Lời giải chi tiết
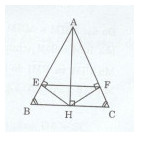
a)Tam giác ABC cân tại A (gt) => AB = AC và \(\widehat {ABC} = \widehat {ACB}.\)
Mà \(\widehat {ABH} + \widehat {BAH} = {90^0}(\Delta ABH\) vuông tại H)
Và \(\widehat {ACH} + \widehat {CAH} = {90^0}(\Delta ACH\) vuông tại H).
Nên \(\widehat {BAH} = \widehat {CAH}.\)
Xét tam giác AEH vuông tại E \((HE \bot AB)\)
Và tam giác AFH vuông tại F \((HF \bot AC)\) có:
AH là cạnh chung.
\(\widehat {EAH} = \widehat {FAH}\) (chứng minh trên).
Do đó: \(\Delta AEH = \Delta AFH\) (cạnh huyền - góc nhọn) => AE = AF.
b)Tam giác AEF có: AE = AF => tam giác AEF cân tại A\(\widehat {AEF} = \widehat {AFE}.\)
Mà \(\widehat {AEF} + \widehat {AFE} + \widehat {EAF} = {180^0}\) (tổng ba góc của một tam giác).
Nên \(\widehat {AEF} + \widehat {AEF} + \widehat {EAF} = {180^0} \to 2\widehat {AEF} + \widehat {EAF} = {180^0} \Rightarrow \widehat {AEF} = {{{{180}^0} - \widehat {EAF}} \over 2}(1)\)
Tam giác ABC có: \(\widehat {ABC} + \widehat {BAC} + \widehat {ACB} = {180^0}\) mà \(\widehat {ABC} = \widehat {ACB}(\Delta ABC\) cân tại A)
Nên \(\widehat {ABC} + \widehat {ABC} + \widehat {BAC} = {180^0} \Rightarrow 2\widehat {ABC} + \widehat {BAC} = {180^0} \Rightarrow \widehat {ABC} = {{{{180}^0} - \widehat {BAC}} \over 2}(2)\)
Từ (1) và (2) suy ra: \(\widehat {AEF} = \widehat {ABC}.\)
Mà góc AEF và ABC đồng vị. Do đó EF // BC.