Bài 19 trang 170 Tài liệu dạy – học Toán 7 tập 1
Giải bài tập Cho tam giác ABC cân tại A.
Đề bài
Cho tam giác ABC cân tại A. Kẻ \(Bx \bot AB\) và \(Cy \bot AC.\) Gọi M là giao điểm của Bx và Cy.
a) Chứng minh rằng \(\Delta ABM = \Delta ACM.\)
b) Chứng minh rằng \(AM \bot BC.\)
c) Kẻ \(BN \bot C(N \in AC),\) gọi I là giao điểm của BN với AM. Chứng minh rằng tam giác BIM cân.
d) Chứng minh rằng \(CI \bot AB.\)
Lời giải chi tiết
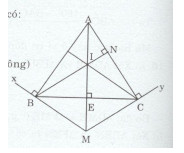
a)Xét tam giác ABM vuông tại B và tam giác ACM vuông tại C có:
AB = AC (tam giác ABC cân tại A)
AM là cạnh chung.
Do đó: \(\Delta ABM = \Delta ACM\) (cạnh huyền - góc nhọn).
b) Xét tam giác BEM và CEM có:
EM là cạnh chung.
\(\eqalign{ & \widehat {EMB} = \widehat {EMC}(\Delta ABM = \Delta ACM) \cr & BM = CM(\Delta ABM = \Delta ACM) \cr} \)
Do đó: \(\Delta BEM = \Delta CEM(c.g.c) \Rightarrow \widehat {BEM} = \widehat {CEM}\)
Mà \(\widehat {BEM} + \widehat {CEM} = {180^0}\) (hai góc kề bù).
Nên \(\widehat {BEM} + \widehat {BEM} = {180^0} \Rightarrow 2\widehat {BEM} = {180^0} \Rightarrow \widehat {BEM} = {90^0}\)
Vậy \(AM \bot BC.\)
c) Ta có: \(BN \bot AC(gt);MC \bot AC(gt)\)
\(\Rightarrow BN//MC \Rightarrow \widehat {BIM} = \widehat {IMC}\) (hai góc so le trong).
Mà \(\widehat {IMC} = \widehat {BMI}(\Delta ABM = \Delta ACM) \Rightarrow \widehat {BIM} = \widehat {BMI}.\)
Do đó: Tam giác BIM cân tại B.
d) Xét tam giác BIM và CIM ta có:
BM = CM \((\Delta ABM = \Delta ACM)\)
IM là cạnh chung.
\(\widehat {BMI} = \widehat {CMI}(\Delta ABM = \Delta ACM)\)
Do đó: \(\Delta BIM = \Delta CIM(c.g.c) \Rightarrow \widehat {BIM} = \widehat {CIM}.\)
Mà \(\widehat {BIM} = \widehat {BMI}\) (chứng minh trên). Do đó: \(\widehat {CIM} = \widehat {BMI}.\)
Mà hai góc CIM và BMI so le trong. Do đó CI // MB.
Mà \(MB \bot AB(gt) \Rightarrow CI \bot AB.\)