Bài 2.20 trang 56 SGK Toán 11 tập 1 - Cùng khám phá
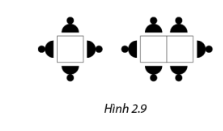
Trong một nhà hàng, một bàn vuông ngồi được 4 người, nếu nối hai bàn vuông lại thì ngồi được 6 người, nối ba bàn ngồi được 8 người, ... Nếu nối n bàn vuông lại theo một hàng ngang thì ngồi được bao nhiêu người?
Đề bài
Trong một nhà hàng, một bàn vuông ngồi được 4 người, nếu nối hai bàn vuông lại thì ngồi được 6 người, nối ba bàn ngồi được 8 người, ... Nếu nối n bàn vuông lại theo một hàng ngang thì ngồi được bao nhiêu người?
Phương pháp giải - Xem chi tiết
Mỗi khi nối thêm 1 bàn thì có thể ngồi thêm 2 người. Từ đó lập cấp số cộng.
Áp dụng công thức \({u_{n + 1}} = {u_1}.{q^n}\) để tính số người khi nối n bàn với nhau.
Lời giải chi tiết
Gọi số người khi ngồi một bàn, khi nối hai bàn, khi nối ba bàn lần lượt là \({u_1},{u_2},{u_3}\).
\( \Rightarrow {u_1} = 4,{u_2} = 6,{u_3} = 8\)
\( \Rightarrow d = {u_2} - {u_1} = 2\)
Ta lập được cấp số cộng với \({u_1} = 4,d = 8\).
Vậy khi nối n bàn lại với nhau thì ngồi được \({u_n} = {u_1} + \left( {n - 1} \right)d = 4 + \left( {n - 1} \right).2 = 2n + 2\) (người).