Bài 3 trang 31 SGK Toán 11 tập 1 - Cánh diều
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:
Đề bài
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:
a) y = sinx trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right),\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
b) y = cosx trên khoảng \(\left( { - 20\pi ; - 19\pi } \right),\left( { - 9\pi ; - 8\pi } \right)\)
Phương pháp giải - Xem chi tiết
Sử dụng khoản biến thiên của hàm số sin x, cos x.
Lời giải chi tiết
a) y = sinx
- Khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
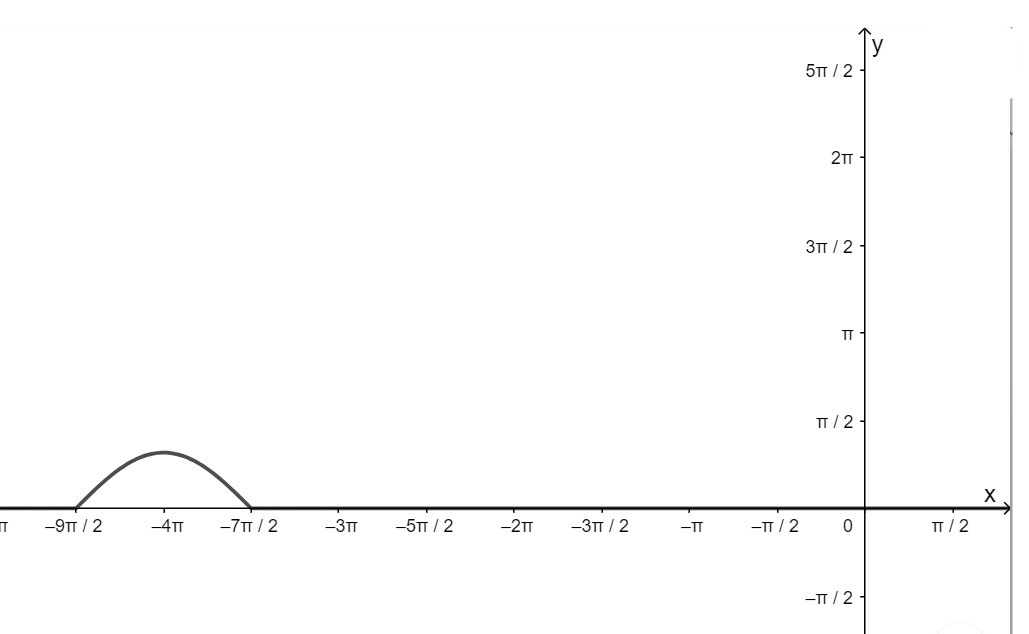
+ Đồng biến trên khoảng \(\left( { - \frac{{9\pi }}{2}; - 4\pi } \right)\)
+ Nghịch biến trên khoảng; \(\left( { - 4\pi ; - \frac{{7\pi }}{2}} \right)\)
- Khoảng \(\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
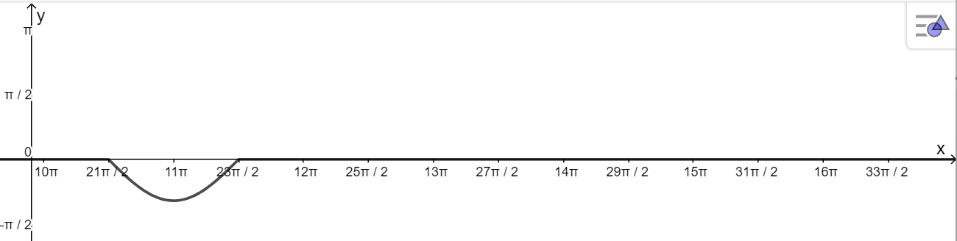
+ Đồng biến trên khoảng: \(\left( {11\pi ;\frac{{23\pi }}{2}} \right)\)
+ Nghịch biến trên khoảng: \(\left( {\frac{{21\pi }}{2};11\pi } \right)\)
b) Xét hàm số \(y = \cos x\):
Do \(\left( { - 20\pi ; - 19\pi } \right) = \left( {0 - 20\pi ;\pi - 20\pi } \right)\)nên hàm số \(y = \cos x\) nghịch biến trên khoảng \(\left( { - 20\pi ; - 19\pi } \right)\)
Do \(\left( { - 9\pi ; - 8\pi } \right) = \left( { - \pi - 8\pi ;0 - 8\pi } \right)\) nên hàm số \(y = \cos x\) đồng biến trên khoảng \(\left( { - 9\pi ; - 8\pi } \right)\)