Bài 4.42 trang 103 SGK Toán 11 tập 1 - Kết nối tri thức
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, AA’. a) Xác định giao điểm của mặt phẳng (MNP) với đường thẳng B‘C b) Gọi K là giao điểm của mặt phẳng (MNP) với đường thẳng B’C. Tính tỉ số (frac{{KB'}}{{KC}})
Đề bài
Cho hình lăng trụ tam giác ABC.A’B’C’ . Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, AA’ .
a) Xác định giao điểm của mặt phẳng ( MNP ) với đường thẳng B‘C.
b) Gọi K là giao điểm của mặt phẳng ( MNP ) với đường thẳng B’C . Tính tỉ số \(\frac{{KB'}}{{KC}}\).
Phương pháp giải - Xem chi tiết
Trường hợp 1: \(\left( \alpha \right)\) chứa đường thẳng \(\Delta \) và cắt đường thẳng d tại I
Khi đó: \(I = d \cap \Delta \Rightarrow I = d \cap \left( \alpha \right)\)
Trường hợp 2: \(\left( \alpha \right)\) không chứa đường thẳng nào d
- Tìm \(\left( \beta \right) \supset d\) và \(\left( \alpha \right) \cap \left( \beta \right) = \Delta \)
- Tìm \(I = d \cap \Delta \)
Suy ra, \(I = d \cap \left( \alpha \right)\).
Lời giải chi tiết
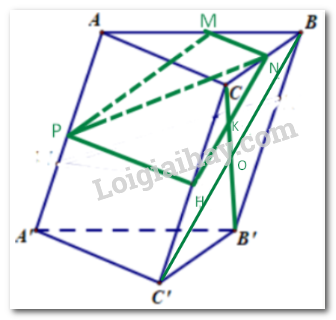
a) Ta có \(\left( {MNP} \right) \cap \left( {ABC} \right) = MN,\left( {ABC} \right) \cap \left( {ACC'A'} \right) = AC,AC//MN\) (do MN là đường trung bình của tam giác ABC ) suy ra giao tuyến của ( MNP ) và ( ACC'A' ) song song với MN và AC.
Qua P kẻ đường thẳng song song với AC cắt CC' tại H.
PH là giao tuyến của ( MNP ) và ( ACC'A' ).
Nối H với N cắt B'C tại K.
Vậy K là giao điểm của ( MNP ) và B'C.
b) Gọi giao điểm BC' và B'C là O.
Ta có ACC'A' là hình bình hành P là trung điểm AA', PH //AC suy ra H là trung điểm CC'.
Xét tam giác CC'B ta có: HN là đường trung bình suy ra CK = OK.
Mà OC = OB' suy ra \(\frac{{KB'}}{{KC}} = 3\).