Bài 4. 43 trang 103 SGK Toán 11 tập 1 - Kết nối tri thức — Không quảng cáo

Đề bài

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trên cạnh SC và cạnh AB lần lượt lấy điểm M và N sao cho CM = 2SM và BN = 2AN .

a) Xác định giao điểm K của mặt phẳng ( ABM ) với đường thẳng SD . Tính tỉ số \(\frac{{SK}}{{SD}}\)

b) Chứng minh rằng MN // (SAD).

Lời giải chi tiết

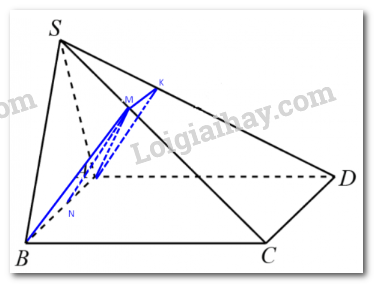
a) Ta có: \(\left( {ABM} \right) \cap \;\left( {ABCD} \right) = AB,\;\left( {ABCD} \right) \cap \;\left( {SCD} \right) = CD,\;AB//CD\).

Suy ra giao tuyến của ( ABM ) và ( SCD ) là đường thẳng qua M song song với AB và CD.

Qua M kẻ MK song song với CD ( K thuộc SD ).

Vậy, K là giao điểm của ( AMN ) và SD.

Xét tam giác SCD ta có: MK //CD suy ra \(\frac{{SK}}{{SD}} = \frac{{SM}}{{SC}} = \frac{1}{3}\)

b) Xét tam giác SCD ta có: MK //CD suy ra \(\frac{{MK}}{{CD}} = \frac{{SM}}{{SC}} = \frac{1}{3}\)

Lại có \(\frac{{AN}}{{AB}} = \frac{1}{3}\) , AB = CD suy ra AN = MK.

Xét tứ giác ANMK ta có: AN = MK , AN // MK suy ra ANMK là hình bình hành.

Do đó MN // AK hay MN // ( SAD ).