Bài 4 trang 106 SGK Toán 11 tập 2 - Cánh Diều
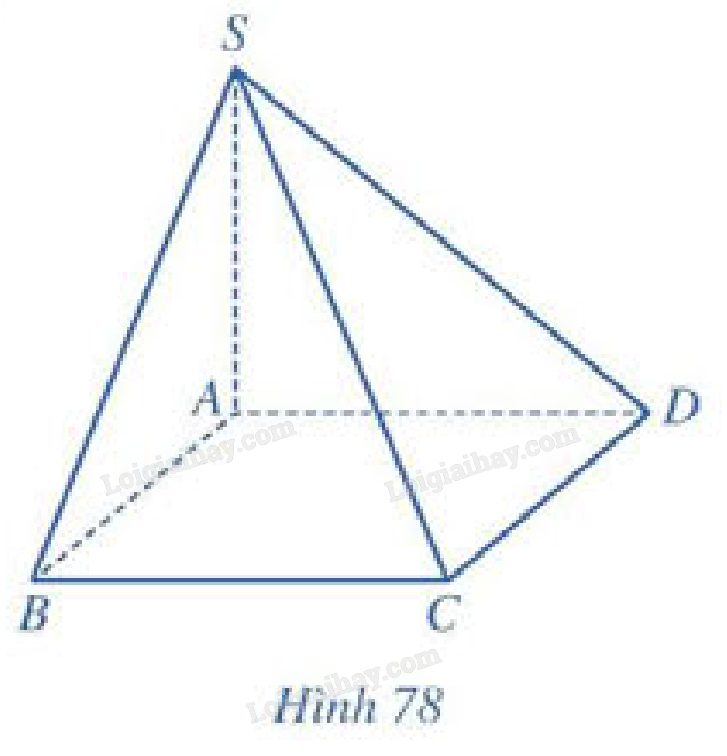
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA = a\) (Hình 78).
Đề bài
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA = a\) ( Hình 78 ).
a) Tính khoảng cách từ điểm \(S\) đến đường thẳng \(C{\rm{D}}\).
b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {SAB} \right)\).
c) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SCD} \right)\).
Phương pháp giải - Xem chi tiết
‒ Cách tính khoảng cách từ một điểm đến một đường thẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên đường thẳng.
‒ Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot C{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{D}} \bot C{\rm{D}}\)
\(\begin{array}{l} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot S{\rm{D}}\\ \Rightarrow d\left( {S,C{\rm{D}}} \right) = S{\rm{D}} = \sqrt {S{A^2} + A{{\rm{D}}^2}} = a\sqrt 2 \end{array}\)
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot A{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{B}} \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SA{\rm{B}}} \right) \Rightarrow d\left( {D,\left( {SAB} \right)} \right) = A{\rm{D}} = a\)
c) Kẻ \(AH \bot S{\rm{D}}\left( {H \in S{\rm{D}}} \right)\).
\(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot AH\)
\( \Rightarrow AH \bot \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = AH\)
Tam giác \(SAD\) vuông tại \(A\) có đường cao \(AH\)
\( \Rightarrow AH = \frac{{SA.A{\rm{D}}}}{{S{\rm{D}}}} = \frac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = \frac{{a\sqrt 2 }}{2}\).