Bài 4 trang 94 SGK Toán 11 tập 1 - Cánh diều
Cho hình chóp S.ABCD có AC cắt BD tại O và AB cắt CD tại P. Điểm M thuộc cạnh SA (M khác S, M khác A). Gọi N là giao điểm của MP và SB, I là giao điểm của MC và DN. Chứng minh rằng S, O, I thẳng hàng
Đề bài
Cho hình chóp S.ABCD có AC cắt BD tại O và AB cắt CD tại P. Điểm M thuộc cạnh SA ( M khác S, M khác A) . Gọi N là giao điểm của MP và SB, I là giao điểm của MC và DN. Chứng minh rằng S, O, I thẳng hàng
Phương pháp giải - Xem chi tiết
Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.
Lời giải chi tiết
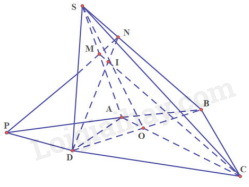
Ta có: DN thuộc (SBD) và MC thuộc (SAC)
Mà MC cắt DN tại I nên I là giao điểm của (SBD) và (SAC)
Ta có: S và O cùng thuộc hai mặt phẳng (SBD) và (SAC)
Theo tính chất 5: Các điểm S, O, I, đều thuộc giao điểm của hai mặt phẳng (SBD) và (SAC)
Vậy ba điểm S, O, I thẳng hàng.