Bài 44 trang 86 SGK Toán 9 tập 2 — Không quảng cáo

Đề bài

Cho tam giác \(ABC\) vuông ở \(A\), có cạnh \(BC\) cố định. Gọi \(I\) là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm \(I\) khi \(A\) thay đổi.

Lời giải chi tiết

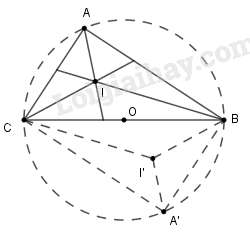
* Dự đoán : Quỹ tích điểm I là cung chứa góc 135º dựng trên đoạn BC.

* Chứng minh :

Phần thuận :

Điểm A luôn nhìn đoạn thẳng AB dưới một góc \(90^\circ \) nên quỹ tích điểm \(A\) là đường tròn đường kính \(BC.\)

Xét tam giác \(ABC\) vuông tại \(A\) nên \(\widehat {ACB} + \widehat {ABC} = 90^\circ \), lại có \(BI\) là phân giác góc \(B\) và \(CI\) là phân giác góc \(C\) nên

\(\widehat {ICB} = \dfrac{1}{2}\widehat {ACB};\,\widehat {IBC} = \dfrac{1}{2}\widehat {ABC} \Rightarrow \widehat {ICB} + \widehat {IBC} = \dfrac{1}{2}\left( {\widehat {ACB} + \widehat {ABC}} \right) = \dfrac{1}{2}.90^\circ  = 45^\circ \)

Xét tam giác \(IBC\) có \(\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = 180^\circ  \Leftrightarrow \widehat {BIC} = 180^\circ  - 45^\circ  = 135^\circ \)

Nên số đo góc \(BIC\) luôn không đổi.

Vậy khi điểm A thay đổi trên đường tròn đường kính BC thì điểm I thay đổi và luôn nhìn đoạn thẳng BC dưới một góc \(135^\circ .\)

Vậy điểm I thuộc hai cung chứa góc \(135^\circ \) dựng trên đoạn BC.

Phần đảo:

Chứng minh mọi điểm I thuộc cung chứa góc 135º dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện.

+ Lấy I trên cung chứa góc 135º dựng trên đoạn BC

+ Kẻ tia Bx sao cho BI là phân giác của góc CBx

+ Kẻ tia Cy sao cho CI là phân giác của góc BCy

+ Bx cắt Cy tại A.

Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC

Ta có:

\(\begin{array}{l} \widehat {BAC} = {180^0} - \left( {\widehat B + \widehat C} \right)\\ = {180^0} - 2\left( {\widehat {IBC} + \widehat {ICB}} \right)\\ = {180^0} - 2\left( {{{180}^0} - \widehat {BIC}} \right)\\ = {180^0} - {360^0} + {2.135^0}\\ = {90^0} \end{array}\)

Vậy ΔABC vuông tại A thỏa mãn đề bài.

Kết luận: Quĩ tích các điểm I là hai cung chứa góc \(135^\circ \) dựng trên đoạn BC.