Bài 43 trang 128 SGK Toán 9 tập 1 — Không quảng cáo

Đề bài

Cho hai đường tròn(O; R) và (O’; r) cắt nhau tại A và $B (R > r)$. Gọi I là trung điểm của OO’. Kẻ đường thẳng vuông góc với IA tại A, đường thẳng này cắt cá đường tròn tâm (O; R) và (O’; r) theo thứ tự tại C và D (khác A).

a) Chứng minh rằng AC = AD.

b) Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng KB vuông góc với AB

Lời giải chi tiết

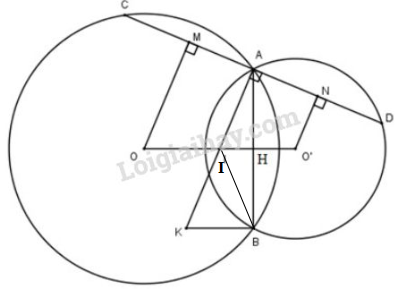
a) Vẽ OM ⊥ AC tại M, O’N ⊥AD tại N.

Xét đường tròn (O), vì $\displaystyle OM \bot AC \Rightarrow MA = MC = {{AC} \over 2}$ (định lý đường kính vuông góc với dây)

Xét đường tròn (O'), vì $\displaystyle O’N ⊥AD \Rightarrow NA = N{\rm{D}} = {{A{\rm{D}}} \over 2}$ (định lý đường kính vuông góc với dây)

Mặt khác, ta có $OM ⊥ CD, IA ⊥ CD, O’N ⊥ CD$

$⇒ OM // IA //O’N.$

Suy ra tứ giác OMNO' là hình thang.

Hình thang OMNO’ có $IA // OM//O'N; IO = IO’$ nên $MA  = NA$ (đường thẳng song song với hai đáy của hình thang và đi qua trung điểm 1 cạnh bên thì đi qua trung điểm cạnh bên còn lại)

Do vậy $2.MA=2.NA$ hay $AC = AD.$

b) Ta có (O) và (O’) cắt nhau tại A, B

⇒ OO’ là đường trung trực của đoạn thẳng AB (tính chất đường nối tâm của hai đường tròn cắt nhau)

$⇒ IA = IB$ (tính chất đường trung trực của đoạn thẳng)

Mặt khác $IA = IK$ ( vì K đối xứng với A qua I)

Do đó: $IA = IB = IK$

Ta có ∆KBA có BI là đường trung tuyến và $\displaystyle BI = {{AK} \over 2}$ nên ∆KBA vuông tại B

$⇒ KB ⊥ AB$