Bài 46 trang 86 SGK Toán 9 tập 2
Dựng một cung chứa góc...
Đề bài
Dựng một cung chứa góc \(55^0\) trên đoạn thẳng \(AB = 3cm.\)
Phương pháp giải - Xem chi tiết
Với đoạn thẳng \(AB\) và góc \(\alpha\, \, (0^0 < \alpha < 180^0)\) cho trước thì quỹ tích các điểm \(M\) thỏa mãn \(\widehat{AMB}=\alpha\) là hai cung chứa góc \(\alpha\) dựng trên đoạn \(AB.\)
Cách vẽ cung chứa góc \( \alpha\) dựng trên đoạn \(AB\).
+ Vẽ tia Ax tạo với AB một góc \( \alpha\)
+ Vẽ đường thẳng \( Ay \bot Ax\).
+ Vẽ đường trung trực d của đoạn thẳng AB. Gọi \( O\) là giao của \( Ay\) với \(d\).
+ Vẽ cung \(AmB\), tâm \(O\), bán kính \(OA\) sao cho cung này nằm ở nửa mặt phẳng bờ \(AB\) không chứa tia \(Ax\).
Cung \(AmB\) là một cung chứa góc \(\alpha\).
Lời giải chi tiết
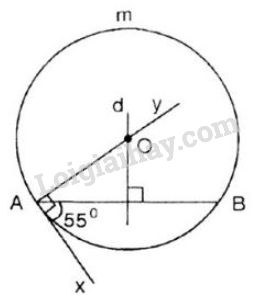
Cách dựng:
- Dựng đoạn thẳng \(AB = 3cm\) (dùng thước đo chia khoảng mm).
- Dựng góc \(\widehat{xAB} = 55^0\) (dùng thước đo góc và thước thẳng).
- Dựng tia \(Ay\) vuông góc với \(Ax\) (dùng êke).
- Dựng đường trung trực \(d\) của đoạn thẳng \(AB\) (dùng thước có chia khoảng và êke). Gọi \(O\) là giao điểm của \(d\) và \(Ay\).
- Dựng đường tròn tâm \(O,\) bán kính \(OA\) (dùng compa).
Ta có: \(\overparen{AmB}\) là cung chứa góc \(55^0\) dựng trên đoạn thẳng \(AB = 3cm\) (một cung).
Chứng minh:
+ O thuộc đường trung trực của AB
⇒ OA = OB
⇒ B thuộc đường tròn (O; OA).
Ax ⊥ AO ⇒ Ax là tiếp tuyến của (O; OA).
⇒ Góc BAx là góc tạo bởi tiếp tuyến Ax và dây AB
Lấy M ∈ cung AmB thì góc AMB là góc nội tiếp chắn cung nhỏ AB
\( \Rightarrow \widehat {BAx} = \widehat {AMB}\)(Góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung)
\(\Rightarrow \widehat {AMB} = {55^0}\)
⇒ \(\overparen{AmB}\) là cung chứa góc 55º dựng trên đoạn AB = 3cm.
Kết luận: Bài toán có một nghiệm hình.