Bài 6 trang 74 SGK Toán 11 tập 2 – Chân trời sáng tạo

Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21,6 m và cạnh đáy dài 34 m.

Đề bài

Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21,6 m và cạnh đáy dài 34 m. Tính độ dài cạnh bên và diện tích xung quanh của kim tự tháp.

Phương pháp giải - Xem chi tiết

Sử dụng định lí Pitago.

Lời giải chi tiết

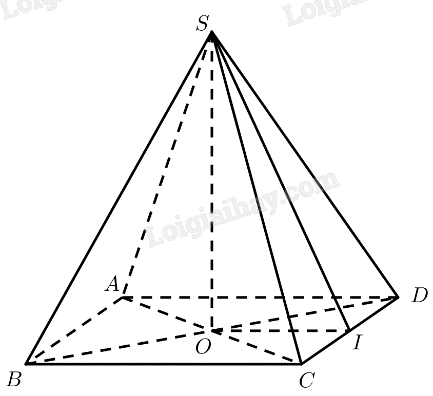
Mô hình hoá hình ảnh kim tự tháp bằng hình chóp tứ giác đều \(S.ABC{\rm{D}}\) có \(O\) là tâm của đáy. Kẻ \(SI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right)\).

Ta có: \(SO = 21,6;C{\rm{D}} = 34\)

\(AC = \sqrt {A{B^2} + B{C^2}} = 34\sqrt 2 \Rightarrow OC = \frac{1}{2}AC = 17\sqrt 2 \)

\(\Delta SOC\) vuông tại \(O\)\( \Rightarrow SC = \sqrt {S{O^2} + O{C^2}} \approx 32,3\)

Vậy độ dài cạnh bên bằng \(32,3\left( m \right)\)

Tam giác \(SCD\) cân tại \(S\)

\( \Rightarrow SI\) vừa là trung tuyến, vừa là đường cao của tam giác

\( \Rightarrow I\) là trung điểm của \(CD\).

Mà \(O\) là trung điểm của \(AD\)

\( \Rightarrow OI\) là đường trung bình của tam giác \(ACD\)

\( \Rightarrow OI = \frac{1}{2}BC = 17\)

\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI\)

\( \Rightarrow \Delta SOI\) vuông tại \(O\)\( \Rightarrow SI = \sqrt {S{O^2} + O{I^2}} \approx 27,5\)