Bài 7. 42 trang 65 SGK Toán 11 tập 2 - Kết nối tri thức — Không quảng cáo

Đề bài

Cho hình hộp $ABCD.A'B'C'D'$ có độ dài tất cả các cạnh bằng $a,AA' \bot (ABCD)$ và $\widehat {BAD} = {60^0}$.

a) Tính thể tích của khối hộp $ABCD.A'B'C'D'$.

b) Tính khoảng cách từ $A$ đến mặt phẳng $\left( {A'BD} \right)$.

Lời giải chi tiết

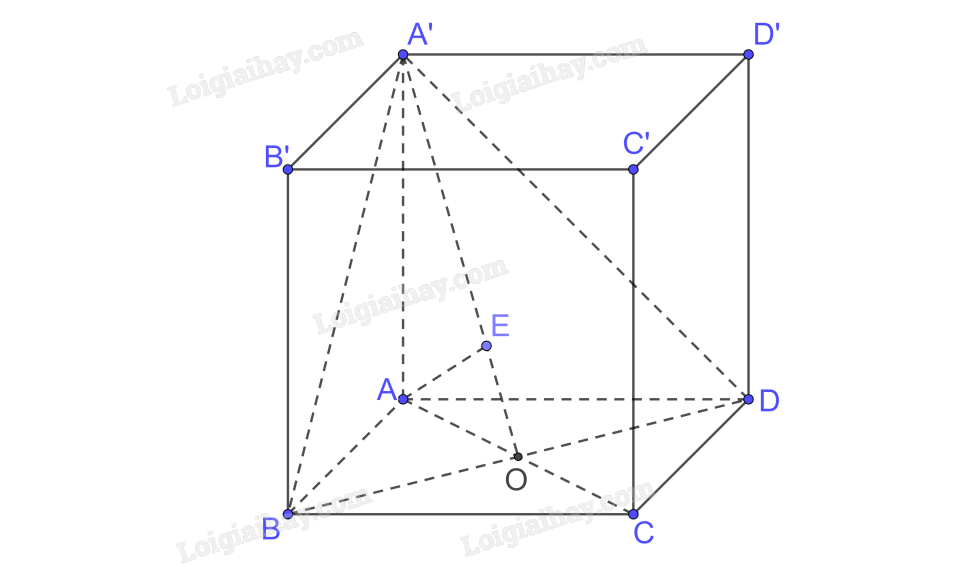
a) Diện tích tam giác ABD bằng diện tích tam giác BCD vì chung đáy BD và chiều cao AO = OC (ABCD là hình thoi)

Diện tích tam giác ABD: ${S_{ABD}} = \frac{1}{2}AB.AD.\sin \widehat {BAD} = \frac{1}{2}a.a.\sin {60^0} = \frac{{{a^2}\sqrt 3 }}{4}$

$\Rightarrow S = 2{S_{ABD}} = \frac{{{a^2}\sqrt 3 }}{2}$

Thể tích khối hộp là $V = AA'.{S_{ABCD}} = a.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{2}$

b) Gọi $AC \cap BD = \left\{ O \right\}$

Ta có $AA' \bot BD,AO \bot BD \Rightarrow BD \bot \left( {A'AO} \right);BD \subset \left( {A'BD} \right) \Rightarrow \left( {A'AO} \right) \bot \left( {A'BD} \right)$

$\left( {A'AO} \right) \cap \left( {A'BD} \right) = A'O$

Trong (A’AO) kẻ $AE \bot A'O$

$\Rightarrow AE \bot \left( {A'BD} \right) \Rightarrow d\left( {A,\left( {A'BD} \right)} \right) = AE$

Xét tam giác ABD có AB = AD và $\widehat {BAD} = {60^0}$ nên tam giác ABD đều

$\Rightarrow OA = \frac{{a\sqrt 3 }}{2}$

Xét tam giác AOA’ vuông tại A có

$\frac{1}{{A{E^2}}} = \frac{1}{{A{{A'}^2}}} + \frac{1}{{O{A^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{7}{{3{a^2}}} \Rightarrow AE = \frac{{a\sqrt {21} }}{7}$

Vậy $d\left( {A,\left( {A'BD} \right)} \right) = \frac{{a\sqrt {21} }}{7}$