Bài 7 trang 56 SGK Toán 11 tập 1 - Cánh diều
Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thể cao xuống với dây đai an toàn buộc xung quanh người)
Đề bài
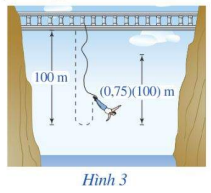
Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thế cao xuống với dây đai an toàn buộc xung quanh người) từ một cây cầu và căng một sợi dây dài 100m. Giả sử sau mỗi lần rơi xuống, người nhảy được kéo lên một quãng đường có độ dài bằng 75% so với lần rơi trước đó và lại bị rơi xuống đúng bằng quãng đường vừa được kéo lên (Hình 3). Tính tổng quãng đường người đó đi được sau 10 lần rơi xuống và lại được kéo lên, tính từ lúc bắt đầu nhảy (làm tròn kết quả đến hàng đơn vị).
Phương pháp giải - Xem chi tiết
Dựa vào công thức cấp số nhân để xác định.
Lời giải chi tiết
Gọi \({u_n}\) là quãng đường người đó rơi xuống lần thứ n.
Khi đó:
\({u_1} = 100\);
\({u_2} = 100.(75\% ) = 75\);
\({u_3} = 100.{(75\% )^2} = 56,25\);
…
Dãy số này lập thành một cấp số nhân có số hạng đầu là 100 và công bội q = 75%, có công thức tổng quát \(u_n = 100.(75\%)^{n-1}\) (m).
Tổng quãng đường người đó đi được khi rơi xuống 10 lần là:
\({S_{10}} = 100.\frac{{1 - {{\left( {75\% } \right)}^n}}}{{1 - 75\% }} \approx 377,47\) (m).
Nhận xét: Người đó sau khi rơi xuống lần 1 thì được kéo lên độ cao bằng quãng đường khi rơi xuống lần 2.
Gọi \({v_n}\) là quãng đường người đó được kéo lên lần thứ n.
Khi đó: \({v_1} = {u_2}\); \({v_2} = {u_3}\);…; \({v_{10}} = {u_{11}}\).
Tổng quãng đường người đó được kéo lên sau 10 lần rơi là:
\(S{'_{10}} = {v_1} + ... + {v_{10}} = {u_2} + ... + {u_{11}}\)
\( = {S_{11}} - {u_1} = 100\frac{{1 - {{(75\% )}^{11}}}}{{1 - 75\% }} - 100 \approx 283,11\) (m).
Vậy tổng quãng đường người đó đi được tính cả rơi xuống và được kéo lên sau 10 lần rơi là khoảng 660 mét.