Bài 83 trang 99 SGK Toán 9 tập 2 — Không quảng cáo

Đề bài

a) Vẽ hình 62 (tạo bởi các cung tròn) với $HI = 10cm$ và $HO = 2cm$. Nêu cách vẽ.

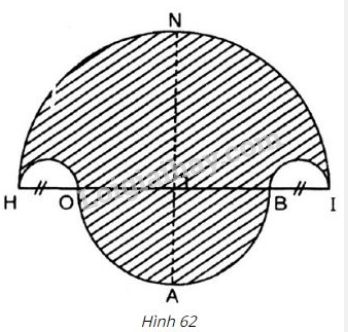
b) Tính diện tích hình $HOABINH$ (miền gạch sọc)

c) Chứng tỏ rằng hình tròn đường kính $NA$ có cùng diện tích với hình $HOABINH$ đó.

Lời giải chi tiết

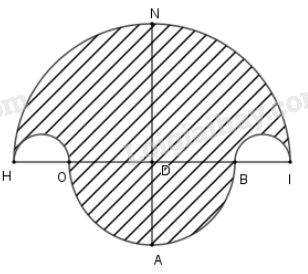
a) + Vẽ đoạn thẳng $HI = 10cm$, trên đoạn $HI$ lấy hai điểm $O$ và $B$ sao cho $HO = BI = 2cm$. Lấy $D$ là trung điểm đoạn thẳng $HI.$

+ Trên cùng một nửa mặt phẳng bờ $HI$, vẽ các nửa đường tròn đường kính $HI;HO;BI$

+ Trên nửa mặt phẳng còn lại ta vẽ nửa đường tròn đường kính $OB.$

+ Vẽ đường trung trực của đoạn $HI$, đường thẳng này cắt nửa đường tròn đường kính $HI$ tại $N$ và cắt nửa đường tròn đường kính $OB$ tại $A.$

+ Bỏ đi hai nửa hình tròn đường kính $HO$ và $BI$, gạch chéo phần hình còn lại vừa vẽ ta được hình theo yêu cầu.

b) Theo cách dựng ta có:

Nửa hình tròn đường kính $HO$ và $BI$ đều có bán kính $r = 2:2 = 1cm$. Hai nửa hình tròn này có diện tích bằng nhau và bằng ${S_3} = \dfrac{1}{2}\pi .{r^2} = \dfrac{1}{2}\pi \,\left( {c{m^2}} \right)$

Nửa hình tròn đường kính $HI$ có bán kính $R = 10:2 = 5cm$ và có tâm $D.$ Nửa hình tròn này có diện tích ${S_1} = \dfrac{1}{2}\pi {R^2} = \dfrac{1}{2}\pi {.5^2} = 12,5\pi \,\left( {c{m^2}} \right)$

Nửa hình tròn đường kính $OB$ có tâm $D$ và có bán kính ${r_2} = OB:2 = \left( {HI - HO - BI} \right):2 = \left( {10 - 2 - 2} \right):2 = 3cm$

Nửa hình tròn này có diện tích bằng ${S_2} = \dfrac{1}{2}\pi r_2^2 = \dfrac{1}{2}\pi {.3^2} = 4,5\pi \left( {c{m^2}} \right)$

Phần hình bị gạch chéo tạo bởi các nửa đường tròn bán kính $5cm;3cm$ và $1cm$.

Diện tích phần bị gạch chéo là $S = {S_1} - 2{S_3} + {S_2} = 12,5\pi  - 2.\dfrac{1}{2}\pi  + 4,5\pi  = 16\pi \left( {c{m^2}} \right)$

Vậy diện tích hình $HOABINH$ là $16\pi \left( {c{m^2}} \right)$

c) Ta có $DN = R = 5cm;\,DA = {r_2} = 3cm \Rightarrow NA = 5 + 3 = 8cm$

Đường tròn đường kính $NA$ có bán kính là $R' = 8:2 = 4cm$

Diện tích hình tròn đường kính $NA$ là $S' = \pi {R'^2} = \pi {.4^2} = 16\pi \left( {c{m^2}} \right)$

Do đó  $S = S'$

Vậy hình tròn đường kính $NA$ có cùng diện tích với hình $HOABINH$ đó.