Bài 99 trang 105 SGK Toán 9 tập 2
Dựng ΔABC, biết BC = 6cm, góc BAC = 80o, đường cao AH có độ dài là 2cm.
Đề bài
Dựng \(ΔABC\), biết \(BC = 6cm\), góc \(\widehat{BAC} = 80^0\), đường cao \(AH\) có độ dài là \(2cm\).
Phương pháp giải - Xem chi tiết
Dựng cung chứa góc \(80^\circ \) trên cạnh \(BC\).
Vẽ đường thẳng song song với \(BC\) và cách \(BC\) khoảng \(2cm\).
Từ đó xác định điểm \(A\) và tam giác \(ABC.\)
Lời giải chi tiết
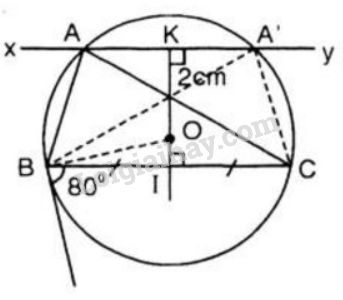
Cách dựng như sau:
- Dựng đoạn \(BC = 6cm\)
- Dựng cung chứa góc \(80^0\) trên đoạn \(BC\) (như bài 46 trang 86)
- Dựng đường thẳng \(xy // BC\) và cách \(BC\) một khoảng là \(2cm\). Đường thẳng \(xy\) cắt cung chứa góc \(80^0\) tại hai điểm \(A\) và \(A’\)
- Tam giác \(ABC\) là tam giác phải dựng thỏa mãn các điều kiện của đề bài
Chứng minh:
+ Theo cách dựng có BC = 6cm.
+ A ∈ cung chứa góc \(80^0\) dựng trên đoạn BC nên \(\widehat {BAC}=80^0\)
+ A ∈ xy song song với BC và cách BC 2cm nên chiều cao \(AH = 2cm.\)
Vậy ΔABC thỏa mãn yêu cầu đề bài.
Biện luận: Do xy cắt cung lớn BC tại hai điểm nên bài toán có hai nghiệm hình (\(∆ABC\) và \(∆A’BC\))