Bài 96 trang 105 SGK Toán 9 tập 2
Cho tam giác ABC nội tiếp đường tròn (O) và tia phân giác của góc A cắt đường tròn tại M.
Đề bài
Cho tam giác \(ABC\) nội tiếp đường tròn \((O)\) và tia phân giác của góc \(A\) cắt đường tròn tại \(M\). Vẽ đường cao \(AH\). Chứng minh rằng:
a) \(OM\) đi qua trung điểm của dây \(BC\).
b) \(AM\) là tia phân giác của góc \(OAH\).
Phương pháp giải - Xem chi tiết
a) + Sử dụng hai góc nội tiếp bằng nhau chắn hai cung bằng nhau
+ Chỉ ra M là điểm chính giữa cung BC.
b) + Chứng minh \(OM//AH\)
+ Sử dụng tính chất hai đường thẳng song song và tính chất tam giác cân.
Lời giải chi tiết
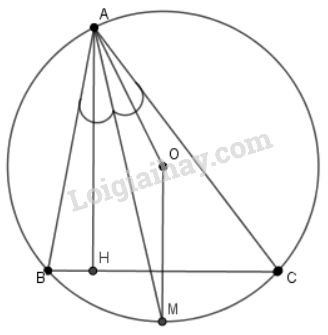

a) Vì \(AM\) là tia phân giác của \(\widehat {BAC}\) nên \(\widehat {BAM} = \widehat {MAC}\)
\( \Rightarrow\) \(\overparen{BM}\)=\(\overparen{MC}\) ( 2 góc nội tiếp bằng nhau thì chắn 2 cung bằng nhau)
\( \Rightarrow\) \(M\) là điểm chính giữa cung \(BC\)
Vậy \(OM \bot BC\) và \(OM\) đi qua trung điểm của \(BC\) (định lí)
b) Ta có : \(OM \bot BC\) và \(AH\bot BC\) nên \(AH//OM\)
\( \Rightarrow \widehat {HAM} = \widehat {AM{\rm{O}}}\) (2 góc so le trong) (1)
Vì \(OA=OM\) (= bán kính đường tròn (O)) nên \(∆OAM\) cân tại \(O\) \( \Rightarrow\) \(\widehat {AM{\rm{O}}} = \widehat {MAO}\) (2)
Từ (1) và (2) \( \Rightarrow\) \(\widehat {HA{\rm{M}}} = \widehat {MAO}\)
Vậy \(AM\) là đường phân giác của góc \(\widehat {OAH}\)