Bài tập 36 trang 98 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho tam giác ABC vuông tại A, BD là phân giác của góc ABC (D thuộc AC).
Đề bài
Cho tam giác ABC vuông tại A, BD là phân giác của góc ABC (D thuộc AC).
Trên nửa mặt phẳng bờ AC không chứa điểm B, qua điểm C vẽ tia Cx vuông góc với CA và cắt tia BD tại E. Chứng minh chu vi tam giác ADB nhỏ hơn chu vi tam giác CDE.
Lời giải chi tiết
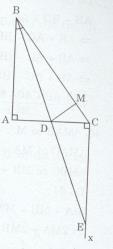
∆ABC vuông tại A. Ta có \(AB \bot AC\) tại A => AB < BC
Trên cạnh BC lấy điểm M sao cho BM = AB
Xét ∆MBD và ∆ABD có: \(\widehat {MBD} = \widehat {ABD}\) (BD là đường phân giác)
MB = AB
BD (cạnh chung)
Do đó ∆MBD = ∆ABD (c.g.c) \( \Rightarrow \widehat {BMD} = \widehat {BAD} = 90^\circ ,AD = MD\)
\(DM \bot BC\) tại M => DM < CD. Nên AD < CD
Mặt khác
\(AB \bot AC,EC \bot AC\)
\( \Rightarrow AB//EC \Rightarrow \widehat {CEB} = \widehat {ABD}\) (so le trong)
Ta có \(\widehat {CEB} = \widehat {MBD}( = \widehat {ABD)}\) => ∆CBE cân tại C => BC = CE
Nên AB < BC = CE
∆ABD vuông tại A => BD 2 = AD 2 + AB 2 (định lí Pythagore)
∆CDE vuông tại E => DE 2 = CD 2 + CE 2
Mà AD < CD và AB < CE. Do đó
BD 2 < DE 2 => BD < DE
Ta có AD + AB + BD < CD + CE + DE
Vậy chu vi tam giác ADB nhỏ hơn chu vi tam giác CDE.