Câu 5 trang 120 SGK Hình học 11 Nâng cao — Không quảng cáo

Đề bài

Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Tính diện tích các tam giác HAB, HBC và HCA.

Lời giải chi tiết

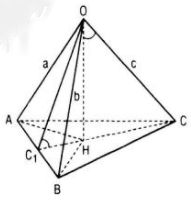
Vì OA, OB, OC đôi một vuông góc và H là hình chiếu của O trên mp(ABC) nên H là trực tâm tam giác ABC. Từ đó HC ₁ ⊥ AB (C ₁ là giao điểm của CH và AB), suy ra OC ₁ ⊥ AB. Như vậy $\widehat {O{C_1}H}$ là góc giữa mp(OAB) và mp(ABC).

Ta có: ${S_{HAB}} = {S_{OAB}}\cos \widehat {O{C_1}H}$

Mà $\widehat {O{C_1}H} = \widehat {HOC}$ nên ${S_{HAB}} = {S_{OAB}}\cos \widehat {HOC}.$

Ta lại có : $\cos \widehat {HOC} = {{OH} \over {OC}},{1 \over {O{H^2}}} = {1 \over {O{A^2}}} + {1 \over {O{B^2}}} + {1 \over {O{C^2}}}$

Từ đó : $\cos \widehat {HOC} = {{ab} \over {\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}$

Mặt khác ${S_{OAB}} = {1 \over 2}ab$

Vậy ${S_{HAB}} = {{{a^2}{b^2}} \over {2\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}$

Tương tự như trên, ta có :

$\eqalign{  & {S_{HBC}} = {{{b^2}{c^2}} \over {2\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}  \cr  & {S_{HAC}} = {{{c^2}{a^2}} \over {2\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }} \cr}$