Dạng 2. Đoạn thẳng, trung điểm của đoạn thẳng Chủ đề 10 Ôn hè Toán 6
Tải về1. Hai đoạn thẳng bằng nhau Đoạn thẳng AB là hình gồm hai điểm A, B và tất cả các điểm nằm giữa giữa A và B.
Lý thuyết
1. Hai đoạn thẳng bằng nhau
Đoạn thẳng AB là hình gồm hai điểm A, B và tất cả các điểm nằm giữa giữa A và B.
Đoạn thẳng AB còn gọi là đoạn thẳng BA.
Hai điểm A, B gọi là hai đầu mút (hoặc hai mút) của đoạn thẳng AB.
2. Độ dài đoạn thẳng
- Mỗi đoạn thẳng có một độ dài. Độ dài đoạn thẳng là một số dương.
- Độ dài đoạn thẳng AB là khoảng cách giữa hai điểm A và B.
- Nếu hai điểm trùng nhau thì khoảng cách giữa chúng bằng 0.
Ví dụ : Đoạn thẳng CD dài 4 cm
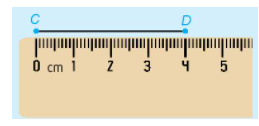
*So sánh hai đoạn thẳng
Ta so sánh hai đoạn thẳng bằng cách so sánh độ dài của chúng.
+ Ta có thể dùng mệnh đề: “Nếu \(AM + MB \ne AB\) thì điểm \(M\) không nằm giữa \(A\) và \(B\)”
+ Nếu điểm \(M\) nằm giữa \(A\) và \(B\); điểm \(N\) nằm giữa \(M\) và \(B\) thì \(AM + MN + NB = AB.\)
3. Trung điểm của đoạn thẳng
Trung điểm của đoạn thẳng là điểm nằm giữa và cách đều hai đầu đoạn thẳng. Trung điểm của đoạn thẳng còn gọi là điểm chính giữa của đoạn thẳng.
Tóm tắt:
\(I\) là trung điểm của đoạn thẳng AB\( \Leftrightarrow \)\({\rm{IA\; = \;IB}}.\) và \(I\) nằm giữa hai điểm A;B.
hoặc \(I\) là trung điểm của đoạn thẳng AB \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{AI + IB = AB}\\{{\rm{IA\; = \;IB}}}\end{array}} \right.\)
hoặc \(I\) là trung điểm của đoạn thẳng AB \( \Leftrightarrow {\rm{AI\; = \;BI\; = }}\dfrac{1}{2}AB\)
Bài tập
Bài 1:
Cho hình vẽ sau:
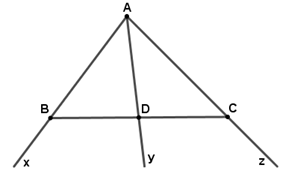
a) Kể tên các đoạn thẳng trên hình vẽ.
b) Những cặp đoạn thẳng nào không cắt nhau?
c) Tia nào cắt đoạn thẳng tại điểm nằm giữa hai đầu của đoạn thẳng đó?
Bài 2:
Cho \(n\) điểm phân biệt \(\left( {n \ge 2,\,n \in \mathbb{N}} \right)\), trong đó không có ba điểm nào thẳng hàng. Vẽ các đoạn thẳng có hai đầu mút là hai trong số các điểm đã cho. Biết vẽ được tất cả \(120\) đoạn thẳng. Tìm giá trị của \(\,n.\)
Bài 3:
Trên tia \(Ox\) lấy hai điểm \(A\) và \(B\) sao cho \(OA = 3cm;\,\,OB = 6cm\).
a) Điểm \(A\) có nằm giữa hai điểm \(O\) và \(B\) không?
b) So sánh \(OA\) và \(AB\).
c) Điểm \(A\) có là trung điểm của đoạn thẳng \(OB\) không? Vì sao?
Bài 4:
Trên đường thẳng \(xy\) lấy một điểm \(O\). Trên tia \(Ox\) lấy điểm \(M\) sao cho \(OM = 2cm\). Trên tia \(Oy\) lấy điểm \(N\) và \(P\) sao cho \(ON = 2cm\) và \(OP = a > 2cm\).
a) Chứng tỏ rằng \(O\) là trung điểm của \(MN\).
b) Tìm giá trị của \(a\) để \(N\) là trung điểm của \(OP\).
Bài 5:
Trên tia \(Ox\) lấy ba điểm \(A,\,\,B,\,\,C\) sao cho \(OA = 2cm\), \(OB = 5cm\) và \(OC = 8cm\).
a) Trong ba điểm \(A,\,\,B,\,\,C\) điểm nào là trung điểm của đoạn thẳng có hai đầu mút là hai điểm còn lại?
b) Gọi \(H,\,\,I,\,\,K\) lần lượt là trung điểm của các đoạn \(OA,\,\,AB,\,\,BC\). Tính độ dài các đoạn thẳng \(HI,\,\,HK\) và \(IK\).
Lời giải chi tiết:
Bài 1:
Cho hình vẽ sau:
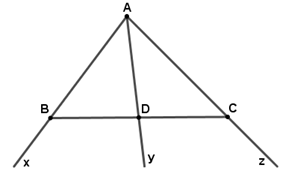
a) Kể tên các đoạn thẳng trên hình vẽ.
b) Những cặp đoạn thẳng nào không cắt nhau?
c) Tia nào cắt đoạn thẳng tại điểm nằm giữa hai đầu của đoạn thẳng đó?
Phương pháp
+ Đoạn thẳng \(AB\) là hình gồm điểm \(A,\,B\) và tất cả các điểm nằm giữa \(AB\).
+ Hai đoạn thẳng cắt nhau có một điểm chung.
Lời giải
a) Các đoạn thẳng có trên hình vẽ là: \(AB,\,\,AD,\,\,AC,\,\,BD,\,\,BC,\,\,DC\)
b) Các cặp đoạn thẳng không cắt nhau là: \(AB\) và \(DC\), \(AC\) và \(BD\)
c) Tia \(Ay\) cắt đoạn thẳng \(BC\) tại điểm \(D\) nằm giữa \(B\) và \(C\).
Bài 2:
Cho \(n\) điểm phân biệt \(\left( {n \ge 2,\,n \in \mathbb{N}} \right)\), trong đó không có ba điểm nào thẳng hàng. Vẽ các đoạn thẳng có hai đầu mút là hai trong số các điểm đã cho. Biết vẽ được tất cả \(120\) đoạn thẳng. Tìm giá trị của \(\,n.\)
Phương pháp
Từ \(n\) điểm \(\left( {n \in \mathbb{N},\,\,n \ge 2} \right)\) ta có thể kẻ được \(\dfrac{{n\left( {n - 1} \right)}}{2}\) đoạn thẳng.
Lời giải
Qua một điểm và \(\left( {n - 1} \right)\) điểm còn lại ta kẻ được \(n - 1\) đoạn thẳng.
Với \(n\) điểm ta kẻ được \(n\left( {n - 1} \right)\) đoạn thẳng.
Nhưng mỗi đoạn thẳng được tính hai lần, số đoạn thẳng kẻ được là \(\dfrac{{n\left( {n - 1} \right)}}{2}\) đoạn thẳng.
Theo đề bài, ta có: \(\dfrac{{n\left( {n - 1} \right)}}{2} = 120\)
\( \Rightarrow n\left( {n - 1} \right) = 120.2\)
\( \Rightarrow n\left( {n - 1} \right) = 240\)
Mà \(240 = 16.15\) nên \(n = 16\).
Vậy \(n = 16\).
Bài 3:
Trên tia \(Ox\) lấy hai điểm \(A\) và \(B\) sao cho \(OA = 3cm;\,\,OB = 6cm\).
a) Điểm \(A\) có nằm giữa hai điểm \(O\) và \(B\) không?
b) So sánh \(OA\) và \(AB\).
c) Điểm \(A\) có là trung điểm của đoạn thẳng \(OB\) không? Vì sao?
Phương pháp
Áp dụng kiến thức:
+) Trên tia \(Ox\) có hai điểm \(M\) và \(N\), \(OM = a,\,\,ON = b\), nếu \(a < b\) thì điểm \(M\) nằm giữa hai điểm \(O\) và \(N\).
+) Điểm \(M\) nằm giữa hai điểm \(A\) và \(B\) thì \(MA + MB = AB\).
+) \(M\) là trung điểm của đoạn thẳng \(AB\) khi và chỉ khi \(AM + MB = AB\) và \(AM = MB\).
Lời giải
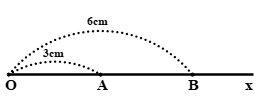
a) Trên tia \(Ox\) ta có \(OA < OB\) (vì \(3cm < 6cm\)) nên điểm \(A\) nằm giữa hai điểm \(O\) và \(B\).
b) Vì điểm \(A\) nằm giữa hai điểm \(O\) và \(B\) nên ta có:
\(OA + AB = OB\)
\( \Rightarrow AB = OB - OA\)\( = 6cm - 3cm = 3cm\)
\( \Rightarrow OA = AB = 3cm\).
Vậy \(OA = AB\).
c) Ta có:
+) Điểm \(A\) nằm giữa hai điểm \(O\) và \(B\).
+) \(OA = AB\)
\( \Rightarrow \) Điểm \(A\) là trung điểm của \(OB\).
Bài 4:
Trên đường thẳng \(xy\) lấy một điểm \(O\). Trên tia \(Ox\) lấy điểm \(M\) sao cho \(OM = 2cm\). Trên tia \(Oy\) lấy điểm \(N\) và \(P\) sao cho \(ON = 2cm\) và \(OP = a > 2cm\).
a) Chứng tỏ rằng \(O\) là trung điểm của \(MN\).
b) Tìm giá trị của \(a\) để \(N\) là trung điểm của \(OP\).
Phương pháp
Áp dụng kiến thức:
+) Trên tia \(Ox\) có hai điểm \(M\) và \(N\), \(OM = a,\,\,ON = b\), nếu \(a < b\) thì điểm \(M\) nằm giữa hai điểm \(O\) và \(N\).
+) Điểm \(M\) nằm giữa hai điểm \(A\) và \(B\) thì \(MA + MB = AB\).
+) \(M\) là trung điểm của đoạn thẳng \(AB\) khi và chỉ khi \(AM + MB = AB\) và \(AM = MB\).
+) Định nghĩa hai tia đối nhau.
Lời giải

a) Vì điểm \(O\) nằm trên đường thẳng \(xy\) nên \(Ox\) và \(Oy\) là hai tia đối nhau.
Vì \(M \in Ox\), \(N \in Oy\) mà \(Ox\) và \(Oy\) là hai tia đối nhau nên điểm \(O\) nằm giữa hai điểm \(M\) và \(N\).
Ta lại có: \(OM = 2cm,\,\,ON = 2cm\)\( \Rightarrow OM = ON\)
\( \Rightarrow \) Điểm \(O\) là trung điểm của đoạn thẳng \(MN\).
b) Trên tia \(Oy\) ta có \(ON < OP\,\,\left( {2\,cm < a\,cm} \right)\) nên điểm \(N\) nằm giữa hai điểm \(O\) và \(P\).
Khi đó, ta có: \(ON + NP = OP\) \( \Rightarrow NP = OP - ON = a - 2\,\,\left( {cm} \right)\)
Để \(N\) là trung điểm của \(OP\) thì \(NP = ON\)\( \Rightarrow a - 2 = 2\)\( \Rightarrow a = 4\,\,\left( {cm} \right)\).
Vậy \(a = 4\,\,\left( {cm} \right)\).
Bài 5:
Trên tia \(Ox\) lấy ba điểm \(A,\,\,B,\,\,C\) sao cho \(OA = 2cm\), \(OB = 5cm\) và \(OC = 8cm\).
a) Trong ba điểm \(A,\,\,B,\,\,C\) điểm nào là trung điểm của đoạn thẳng có hai đầu mút là hai điểm còn lại?
b) Gọi \(H,\,\,I,\,\,K\) lần lượt là trung điểm của các đoạn \(OA,\,\,AB,\,\,BC\). Tính độ dài các đoạn thẳng \(HI,\,\,HK\) và \(IK\).
Phương pháp
Áp dụng kiến thức:
+) Trên tia \(Ox\) có hai điểm \(M\) và \(N\), \(OM = a,\,\,ON = b\), nếu \(a < b\) thì điểm \(M\) nằm giữa hai điểm \(O\) và \(N\).
+) Điểm \(M\) nằm giữa hai điểm \(A\) và \(B\) thì \(MA + MB = AB\).
+) \(M\) là trung điểm của đoạn thẳng \(AB\) khi và chỉ khi \(AM + MB = AB\) và \(AM = MB\).
Lời giải
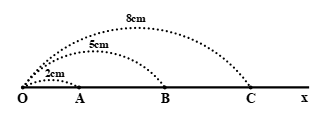
a) Trên tia \(Ox\) ta có \(OA < OB\,\,\left( {2\,cm < 5\,cm} \right)\) nên điểm \(A\) nằm giữa hai điểm \(O\) và \(B\).
Ta có: \(OA + AB = OB\)\( \Rightarrow AB = OB - OA\)\( = 5cm - 2cm = 3cm\)
Trên tia \(Ox\) ta có \(OB < OC\,\,\left( {5\,cm < 8\,cm} \right)\) nên điểm \(B\) nằm giữa hai điểm \(O\) và \(C\).
Ta có: \(OB + BC = OC\)\( \Rightarrow BC = OC - OB\)\( = 8cm - 5cm = 3cm\)
\( \Rightarrow AB = BC = 3cm\)
Trên tia \(Ox\) ta có \(OA < OB < OC\) \(\left( {2cm < 5cm < 8cm} \right)\) nên điểm \(B\) nằm giữa hai điểm \(A\) và \(C\).
Ta có: điểm \(B\) nằm giữa hai điểm \(A,\,\,C\) và \(AB = BC = 3cm\)
\( \Rightarrow \) Điểm \(B\) là trung điểm của đoạn thẳng \(AC\).
b) Ta có hình vẽ:

Vì:
+ Điểm \(H\) là trung điểm của \(OA\) nên \(OH = HA = \dfrac{{OA}}{2} = \dfrac{2}{2} = 1\,\,\left( {cm} \right)\).
+ Điểm \(I\) là trung điểm của \(AB\) nên \(AI = IB = \dfrac{{AB}}{2} = \dfrac{3}{2} = 1,5\,\,\left( {cm} \right)\).
+ Điểm \(K\) là trung điểm của \(BC\) nên \(BK = KC = \dfrac{{BC}}{2} = \dfrac{3}{2} = 1,5\,\,\left( {cm} \right)\).
Do \(H\) và \(I\) thuộc hai tia đối nhau gốc \(A\) nên điểm \(A\) nằm giữa \(H\) và \(I\). Ta có:
\(HA + AI = HI\) \( \Rightarrow HI = 1cm + 1,5cm = 2,5cm\)
Do \(K\) và \(I\) thuộc hai tia đối nhau gốc \(B\) nên điểm \(B\) nằm giữa \(K\) và \(I\). Ta có:
\(IB + BK = IK\) \( \Rightarrow KI = 1,5cm + 1,5cm = 3cm\)
Ta có:
+ Điểm \(A\) nằm giữa \(H\) và \(I\) nên \(H\) và \(A\) nằm cùng phía so với điểm \(I\).
+ Điểm \(B\) nằm giữa \(K\) và \(I\) nên \(K\) và \(B\) nằm cùng phía so với điểm \(I\).
+ Điểm \(I\) nằm giữa \(A\) và \(B\) nên \(B\) và \(A\) nằm khác phía so với điểm \(I\).
Suy ra, \(H\) và \(K\) nằm khác phía so với điểm \(I\).
Suy ra, điểm \(I\) nằm giữa hai điểm \(H\) và \(K\).
Ta có: \(IH + IK = HK\)\( \Rightarrow HK = 2,5cm + 3cm = 5,5cm\).