Đề kiểm tra 15 phút - Đề số 10 - Bài 5 - Chương 3 - Hình học 9

Giải Đề kiểm tra 15 phút - Đề số 10 - Bài 5 - Chương 3 - Hình học 9

Đề bài

Cho đường tròn (O; R) đường kính BC. Lấy A là điểm chính giữa của cung BC. D là điểm di động trên cung AC, AD cắt BC tại E. Xác định vị trí điểm D để \(2AD + AE\) nhỏ nhất.

Phương pháp giải - Xem chi tiết

Sử dụng:

+Số đo góc có đỉnh bên ngoài đường tròn

+Số đo góc nội tiếp bằng nửa cung bị chắn

+ Tam giác đồng dạng

+ Định lý Py-ta go

+BĐT Cô-si cho 2 số dương

Lời giải chi tiết

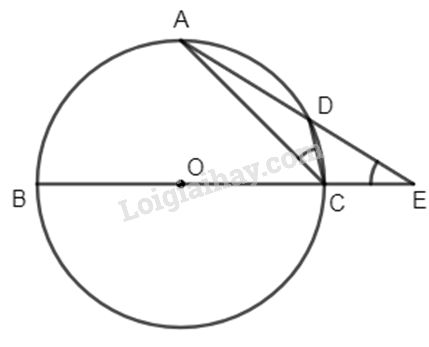
Ta có :

\(\widehat {AEC} = \dfrac{{sd\overparen{AB} - sd\overparen{CD}} }{ 2} \)\(\,= \dfrac{{sd\overparen{AC} - sd\overparen{CD}}}{ 2} = \dfrac{{sd\overparen{AD}} }{ 2}\) ( vì \(\overparen{AB} = \overparen{AC}\) )

Lại có \(\widehat {ACD} = \dfrac{{sd\overparen{AD}}}{2} \Rightarrow \widehat {AEC} = \widehat {ACD}\)

\( \Rightarrow ∆ACD\) và \(∆AEC\) đồng dạng (g.g)

\( \Rightarrow \dfrac{{AD} }{ {AC}} =\dfrac {{AC} }{{AE}} \Rightarrow A{C^2} = AD.AE\)

\(∆ABC\) vuông cân ( chắn nửa đường tròn) có \(BC = 2R.\)

Đặt \(AB = AC = x.\)

Theo định lí Py-ta-go:

\(\eqalign{ & {x^2} + {x^2} = {\left( {2R} \right)^2} \Rightarrow 2{x^2} = 4{R^2} \cr & \Rightarrow {x^2} = 2{R^2} \Rightarrow x = R\sqrt 2 \cr} \)

Vậy \(AB = AC = R\sqrt 2 \)

\( \Rightarrow {\left( {R\sqrt 2 } \right)^2} = AD.AE \)

\(\Rightarrow AD.AE = 2{R^2}.\)

Áp dụng bất đẳng thức Côsi cho hai số dương, ta có :

\(2AD + AE \ge 2\sqrt {2AD.AE} \)