Đề kiểm tra 15 phút Toán 6 Chân trời sáng tạo - Đề số 1
Đề bài
Phát biểu nào sau đây đúng ?
-
A.
Nếu \(x \in \mathbb{N}\) thì \(x \notin \mathbb{N}^*\)
-
B.
Nếu \(x \in \mathbb{N}\) thì \(x \in \mathbb{N}^*\)
-
C.
Nếu \(x \notin \mathbb{N}^*\) thì \(x \notin \mathbb{N}\)
-
D.
Nếu \(x \in \mathbb{N}^*\) thì \(x \in \mathbb{N}\)
Dùng ba chữ số \(0;4;6\) để viết tập hợp các số có ba chữ số khác nhau. Hỏi tập này có bao nhiêu phần tử?
-
A.
\(3\)
-
B.
\(4\)
-
C.
\(2\)
-
D.
\(5\)
Chọn câu sai .
-
A.
\({a^m}.{a^n} = {a^{m + n}}\)
-
B.
\({a^m}:{a^n} = {a^{m - n}}\) với $ m \ge n$ và $ a\ne 0$
-
C.
\({a^0} = 1\)
-
D.
\({a^1} = 0\)
\(789 \times 123\) bằng:
-
A.
97047
-
B.
79047
-
C.
47097
-
D.
77047
Khối lớp 6 của một trường có 255 học sinh đi dã ngoại. Cô phụ trách muốn chia đều các học sinh của khối 6 thành 9 nhóm. Hỏi cô chia như vậy đúng hay sai?
Đúng
Sai
Giá trị của biểu thức \(2\left[ {\left( {195 + 35:7} \right):8 + 195} \right] - 400\) bằng
-
A.
$140$
-
B.
$60$
-
C.
$80$
-
D.
$40$
Cho hình vẽ sau:
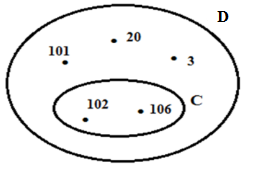
Viết tập hợp C và D.
-
A.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {20;101;102;106} \right\}\)
-
B.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {3;20;102;106} \right\}\)
-
C.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {3;20;101} \right\}\)
-
D.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {3;20;101;102;106} \right\}\)
Không tính giá trị cụ thể, hãy so sánh \(A = 1987657.1987655\) và \(B = 1987656.1987656\)
-
A.
\(A > B\)
-
B.
\(A < B\)
-
C.
\(A \le B\)
-
D.
\(A = B\)

Điền số thích hợp vào ô trống:
\(161291 + \)
\(= (6000 + 725) + 161291\)
Để đánh số các trang của một quyển sách người ta phải dùng tất cả \(600\) chữ số. Hỏi quyển sách có bao nhiêu trang?
-
A.
\(326\)
-
B.
\(136\)
-
C.
\(263\)
-
D.
\(236\)
Lời giải và đáp án
Phát biểu nào sau đây đúng ?
-
A.
Nếu \(x \in \mathbb{N}\) thì \(x \notin \mathbb{N}^*\)
-
B.
Nếu \(x \in \mathbb{N}\) thì \(x \in \mathbb{N}^*\)
-
C.
Nếu \(x \notin \mathbb{N}^*\) thì \(x \notin \mathbb{N}\)
-
D.
Nếu \(x \in \mathbb{N}^*\) thì \(x \in \mathbb{N}\)
Đáp án : D
\(\mathbb{N}^*\) là tập hợp các số tự nhiên khác 0.
\(\mathbb{N}\) là tập hợp các số tự nhiên khác.
Đáp án A sai vì: 1 thuộc \(\mathbb{N}\) và cũng thuộc \(\mathbb{N}^*\) .
Đáp án B sai vì: 0 thuộc \(\mathbb{N}\) nhưng không thuộc \(\mathbb{N}^*\)
Đáp án C sai vì: 0 không thuộc \(\mathbb{N}^*\) nhưng 0 thuộc \(\mathbb{N}\) .
Đáp án D đúng vì: \(x \in \mathbb{N}^*\) có nghĩa là x là số tự nhiên khác 0, khi đó x là số tự nhiên, hay x thuộc \(\mathbb{N}\) .
Dùng ba chữ số \(0;4;6\) để viết tập hợp các số có ba chữ số khác nhau. Hỏi tập này có bao nhiêu phần tử?
-
A.
\(3\)
-
B.
\(4\)
-
C.
\(2\)
-
D.
\(5\)
Đáp án : B
+ Viết các số có ba chữ số khác nhau lập thành từ ba chữ số \(0;4;6\)
+ Đếm các số viết được ta được số phần tử của tập hợp
Với ba chữ số \(0;4;6\) ta có thể lập được bốn số có ba chữ số khác nhau là \(640;604;406;460\) . Do đó tập hợp cần tìm có bốn phần tử.
Chọn câu sai .
-
A.
\({a^m}.{a^n} = {a^{m + n}}\)
-
B.
\({a^m}:{a^n} = {a^{m - n}}\) với $ m \ge n$ và $ a\ne 0$
-
C.
\({a^0} = 1\)
-
D.
\({a^1} = 0\)
Đáp án : D
Sử dụng các công thức chia hai lũy thừa cùng cơ số; nhân hai lũy thừa cùng cơ số và các qui ước
Ta có với $ a,m,n \in N$ thì
+ \({a^m}.{a^n} = {a^{m + n}}\) nên A đúng
+ \({a^m}:{a^n} = {a^{m - n}}\) với $ m \ge n$ và $ a\ne 0$ nên B đúng
+ $a^0=1$ nên C đúng.
+ \({a^1} = a\) nên D sai.
\(789 \times 123\) bằng:
-
A.
97047
-
B.
79047
-
C.
47097
-
D.
77047
Đáp án : A
Đặt tính rồi tính.
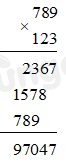
Vậy \(789 \times 123 = 97047\)
Khối lớp 6 của một trường có 255 học sinh đi dã ngoại. Cô phụ trách muốn chia đều các học sinh của khối 6 thành 9 nhóm. Hỏi cô chia như vậy đúng hay sai?
Đúng
Sai
Đúng
Sai
Số học sinh chia đều được 9 nhóm nếu số học sinh chia hết cho 9.
Ta có 255 có tổng các chữ số bằng 2+5+5=12 không chia hết cho 9 nên cô phụ trách không thể chia đều số học sinh thành 9 nhóm được.
Giá trị của biểu thức \(2\left[ {\left( {195 + 35:7} \right):8 + 195} \right] - 400\) bằng
-
A.
$140$
-
B.
$60$
-
C.
$80$
-
D.
$40$
Đáp án : D
Thực hiện phép tính trong ngoặc tròn rồi đến ngoặc vuông. Sau đó là phép nhân và phép trừ.
Ta có \(2\left[ {\left( {195 + 35:7} \right):8 + 195} \right] - 400\)
\( = 2\left[ {\left( {195 + 5} \right):8 + 195} \right] - 400\)
\( = 2\left[ {200:8 + 195} \right] - 400\)
\( = 2\left( {25 + 195} \right) - 400\)
\( = 2.220 - 400\)
\( = 440 - 400\)
\( = 40\)
Cho hình vẽ sau:

Viết tập hợp C và D.
-
A.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {20;101;102;106} \right\}\)
-
B.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {3;20;102;106} \right\}\)
-
C.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {3;20;101} \right\}\)
-
D.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {3;20;101;102;106} \right\}\)
Đáp án : D
Các phần tử trong vòng tròn là các phần tử thuộc tập hợp.
Từ hình vẽ ta viết các tập hợp dưới dạng liệt kê.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {3;20;101;102;106} \right\}\)
Không tính giá trị cụ thể, hãy so sánh \(A = 1987657.1987655\) và \(B = 1987656.1987656\)
-
A.
\(A > B\)
-
B.
\(A < B\)
-
C.
\(A \le B\)
-
D.
\(A = B\)
Đáp án : B
Áp dụng tính chất phân phối giữa phép nhân với phép cộng để biến đổi và so sánh \(A,B.\)
Ta có \(A = 1987657.1987655\)\( = \left( {1987656 + 1} \right).1987655\)\( = 1987656.1987655 + 1987655\,\,\,\left( 1 \right)\)
Và \(B = 1987656.\left( {1987655 + 1} \right)\) \( = 1987656.1987655 + 1987656\,\,\,\left( 2 \right)\)
Vì \(1987655 < 1987656\) và từ (1) và (2) suy ra \(A < B.\)

Điền số thích hợp vào ô trống:
\(161291 + \)
\(= (6000 + 725) + 161291\)
\(161291 + \)
\(= (6000 + 725) + 161291\)
Áp dụng tính chất giao hoán của phép cộng: Khi đổi chỗ các số hạng trong một tổng thì tổng đó không thay đổi.
Ta có: \((6000 + 725) + 161291 = 6725 + 161291\)
Hay \(161291 + 6725 = (6000 + 725) + 161291\)
Vậy đáp án đúng điền vào ô trống là \(6725\).
Để đánh số các trang của một quyển sách người ta phải dùng tất cả \(600\) chữ số. Hỏi quyển sách có bao nhiêu trang?
-
A.
\(326\)
-
B.
\(136\)
-
C.
\(263\)
-
D.
\(236\)
Đáp án : D
Chia ra thành các trang đánh \(1\) chữ số; \(2\) chữ số và \(3\) chữ số để tìm số trang của quyển sách.
\(99\) trang đầu cần dùng \(9.1 + 90.2 = 189\) chữ số
\(999\) trang đầu cần dùng \(9.1 + 90.2 + 900.3 = 2889\) chữ số
Vì \(189 < 600 < 2889\) nên trang cuối cùng phải có ba chữ số
Số chữ số dùng để đánh số trang có ba chữ số là \(600 - 189 = 411\) (chữ số)
Số trang có ba chữ số là \(411:3 = 137\) trang
Số trang của quyển sách là \(99 + 137 = 236\) trang