Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 3 - Hình học 9 — Không quảng cáo

Đề bài

Bài 1: Cho hình vuông ABCD cạnh a. Lấy M thuộc cạnh AB, N thuộc cạnh AD sao cho $\widehat {MCN} = 45^\circ$. Gọi E, F lần lượt là giao điểm của CM và CN với BD.

a) Chứng minh tứ giác DCEN nội tiếp.

b) Gọi H là giao điểm của MF và NE. Chứng minh CH vuông góc với MN tại I.

c) Chứng minh MN là tiếp tuyến của đường tròn ngoại tiếp ∆DIB.

Bài 2: Cho đường tròn (O; R) và ba điểm A, B, C sao cho $sđ\overparen{AC} =30^o$, dây cung $AB = R\sqrt 3$ và AB, AC ở về hai phía AO.

a) Tính độ dài cung CAB theo R.

b) Chứng minh : OC // AB.

LG bài 1

Phương pháp giải:

a.Chứng minh tứ giác DCNE và BCFM nội tiếp và H là trực tâm của tam giác CMN

b.Chứng minh tứ giác MEFN và BCFMN nội tiếp, từ đó chứng minh CI=CB và MN vuông góc với CH

Lời giải chi tiết:

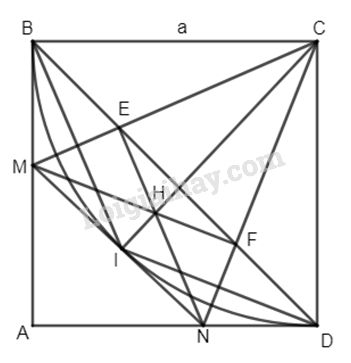
Ta có $\widehat {ECN} = \widehat {EDN} = 45^\circ$ $\Rightarrow$ Bốn điểm D, C, E, N cùng thuộc một đường tròn hay tứ giác DCEN nội tiếp.

a)Tứ giác DCEN nội tiếp (cmt) mà $\widehat {CDN} = 90^\circ$(gt)

$\Rightarrow \widehat {CEN} = 90^\circ$ hay $NE \bot CM.$

Tương tự ta chứng minh được tứ giác BCFM nội tiếp ( $\widehat {MBF} = \widehat {MCF} = 45^\circ$)

$\Rightarrow \widehat {MFC} = \widehat {MBC} = 90^\circ$ hay $MF \bot CN$ mà MF và NE giao nhau tại H nên H là trực tâm ∆CMN.

$\Rightarrow$ CH là đường cao hay $CH \bot MN.$

b) Ta có tứ giác MEFN nội tiếp ( $\widehat {MEN} = \widehat {MFN} = 90^\circ$)

$\Rightarrow \widehat {CMI} = \widehat {CFB}$ ( cùng bù với $\widehat {NFE}$ )

Lại có tứ giác BCFM nội tiếp (cmt)

$\Rightarrow \widehat {CMB} = \widehat {CFB}$ ( góc nội tiếp cùng chắn cung BC) $\Rightarrow \widehat {CMI} = \widehat {CMB}$

Do đó $∆CBM = ∆CIM$ ( cạnh huyền – góc nhọn)

$\Rightarrow  CI = CB = a$ mà $MN \bot CH$ tại I (cmt) nên MN là tiếp tuyến của đườn tròn ngoại tiếp ∆DIB có tâm C và bán kính bằng a.

LG bài 2

Phương pháp giải:

Sử dụng:

+ Số đo của góc nội tiếp bằng số đo của cung bị chắn

+Công thức: $l = \frac{{\pi Rn}}{{180}}$

Lời giải chi tiết:

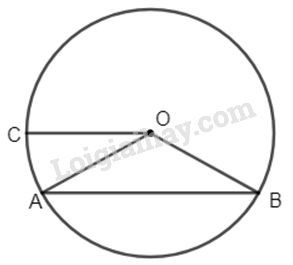
a) Ta có :$AB = R\sqrt 3  \Rightarrow \widehat {AOB} = 120^\circ$

$sđ\overparen{AC} = 30^o \Rightarrow  \widehat {AOC} = 30^\circ$.

Vậy $\widehat {BOC} = 150^\circ$.

Khi đó ${l_{\overparen {BAC}}} = \dfrac{{\pi R.150} }{ {180}} =\dfrac {{5\pi R} }{ 6}$.

b)      ∆AOB cân tại O có $\widehat {AOB} = 120^\circ$

$\Rightarrow \widehat {OAB} = \widehat {OBA} =\dfrac {{180^\circ  - 120^\circ }}{2}$$\, = 30^\circ$

Do đó $\widehat {OAB} = \widehat {AOC} = 30^\circ$

$\Rightarrow$ OC // AB ( cặp góc so le trong bằng nhau).