Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương 2 - Đại số 9 — Không quảng cáo

Đề bài

Bài 1. Tìm điều kiện xác định của hàm số:

a. \(y = {1 \over {x - 1}}\)

b. \(y = \sqrt {1 - x} \)

Bài 2. Chứng minh rằng hàm số \(y = f\left( x \right) =  - x + 1\) nghịch biến trên \(\mathbb R\) .

So sánh \(f\left( {1 - \sqrt 2 } \right)\) và \(f\left( {1 + \sqrt 2 } \right)\)

Bài 3. Cho hàm số \(y = \sqrt 2 x + 1\)

a. Vẽ đồ thị (d) của hàm số

b. Tính góc tạo bởi (d) và trục Ox (làm tròn đến phút)

c. Viết phương trình đường thẳng (d’) qua O và song song với đường thẳng \(y = \sqrt 2 x + 1\)

LG bài 1

Phương pháp giải:

Hàm số \(\dfrac {1}{A}\) xác định khi \(A\ne 0\)

Hàm số \(\sqrt A\) xác định khi \(A\ge 0\)

Lời giải chi tiết:

a. \({1 \over {x - 1}}\) xác định \(⇔ x – 1 ≠ 0 ⇔ x ≠ 1\).

b. \(\sqrt {1 - x} \) xác định \(⇔ 1 – x ≥ 0 ⇔ x ≤ 1\).

LG bài 2

Phương pháp giải:

Giả sử \({x_1} < {x_2}\) và \({x_1},{x_2} \in \mathbb R\). Xét hiệu \(H = f\left( {{x_1}} \right) - f\left( {{x_2}} \right)\).

+ Nếu \(H < 0\) thì hàm số đồng biến trên \(\mathbb R \)

+ Nếu \(H > 0\) thì hàm số nghịch biến trên \(\mathbb R \)

Lời giải chi tiết:

Với \({x_1},{\rm{ }}{x_2}\) bất kì thuộc \(\mathbb R\) và \({x_1} < {\rm{ }}{x_2}\). Ta có:

\(\eqalign{  & f\left( {{x_1}} \right) =  - {x_1} + 1;f\left( {{x_2}} \right) =  - {x_2} + 1\cr& \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) =  - \left( {{x_1} - {x_2}} \right)  \cr  & \text{Vì }{x_1} < {x_2} \Rightarrow {x_1} - {x_2} < 0 \cr&\Rightarrow  - \left( {{x_1} - {x_2}} \right) > 0  \cr  &  \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right) \cr} \)

Vậy hàm số đã cho nghịch biến trên \(\mathbb R\).

Ta có: \(1 - \sqrt 2  < 1 + \sqrt 2 \) và hàm số \(y = f\left( x \right) =  - x + 1\) nghịch biến \( \Rightarrow f\left( {1 - \sqrt 2 } \right) > f\left( {1 + \sqrt 2 } \right)\)

LG bài 3

Phương pháp giải:

a) Xác định tọa độ 2 điểm thuộc đồ thị hàm số rồi vẽ đường thẳng đi qua hai điểm đó

b) Tính góc dựa vào tỉ số lượng giác của góc nhọn

c) Hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) song song với nhau khi và chỉ khi \(a = a', b ≠ b'\).

Lời giải chi tiết:

a. Bảng giá trị:

Đồ thị của hàm số là đường thẳng (d) đi qua hai điểm \(A\left( { - \sqrt 2 ; - 1} \right)\) và \(B(0; 1)\).

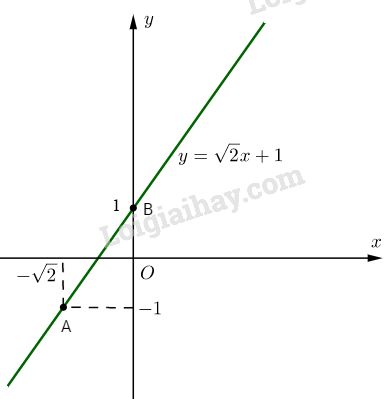
b. Trong tam giác ABC với \(C(0 ; -1)\), ta có:

\(\tan \widehat {BAC} = {2 \over {\sqrt 2 }} = \sqrt 2\)

\(  \Rightarrow \widehat {BAC} = 54^\circ 44'\)

Ta có: \(\widehat {BDO} = \widehat {BAC} = \alpha  \Rightarrow \alpha  \approx 54^\circ 44'\)

c. Phương trình (d’) có dạng: \(y = \sqrt 2 x + b\,\left( {b \ne 1} \right)\)

\(O ∈ (d’) ⇒ b = 0\). Vậy \(y = \sqrt 2 x\)