Đề kiểm tra học kì 1 Toán 6 Kết nối tri thức - Đề số 4
Đề bài
Viết tập hợp A các số tự nhiên lớn hơn \(5\) và nhỏ hơn \(10.\)
-
A.
\(A = \left\{ {6;7;8;9} \right\}.\)
-
B.
\(A = \left\{ {5;6;7;8;9} \right\}.\)
-
C.
\(A = \left\{ {6;7;8;9;10} \right\}.\)
-
D.
\(A = \left\{ {6;7;8} \right\}.\)
-
A.
Chiếc bàn có tâm đối xứng
-
B.
Chiếc bàn có trục đối xứng
-
C.
Chiếc bàn vừa có tâm đối xứng và trục đối xứng
-
D.
Chiếc bàn không có tâm đối xứng và trục đối xứng
Thay dấu * để được số nguyên tố $\overline {3*} $:
-
A.
$7$
-
B.
$4$
-
C.
$6$
-
D.
$9$
Cho \(\overline {55a62} \) chia hết cho 3. Số thay thế cho \(a\) có thể là
-
A.
1
-
B.
2
-
C.
3
-
D.
5
Cho tổng \(M = 75 + 120 + x\) . Với giá trị nào của \(x\) dưới đây thì \(M \, \vdots \, 3?\)
-
A.
$7$
-
B.
$5$
-
C.
$4$
-
D.
$12$
Cho n là một số tự nhiên lớn hơn 2 và nhỏ hơn 5. Khẳng định nào sau đây đúng ?
-
A.
n nằm bên phải điểm 5 trên tia số
-
B.
n nằm bên trái điểm 2 trên tia số
-
C.
n nằm bên phải điểm 2 trên tia số
-
D.
n nằm bên phải điểm 5 và cách điểm 5 một đơn vị trên tia số.
Cho tam giác đều \(MNP\) có \(MN = 5\,cm\), khẳng định nào sau đây đúng?
-
A.
\(NP = 3\,cm\)
-
B.
\(MP = 4\,cm\)
-
C.
\(NP = 6\,cm\)
-
D.
\(MP = 5\,cm\)
$BCNN(9;24)$ là bao nhiêu?
-
A.
$54$
-
B.
$18$
-
C.
$72$
-
D.
$36$
Trong các số sau, số nào vừa chia hết cho 2 vừa chia hết cho 5?
-
A.
550
-
B.
9724
-
C.
7905
-
D.
5628
Cho \(x - 236\) là số đối của số 0 thì x là:
-
A.
\( - 234\)
-
B.
\(234\)
-
C.
\(0\)
-
D.
\(236\)
Trong các câu sau câu nào sai:
-
A.
Hình vuông có đúng 4 trục đối xứng
-
B.
Hình thoi, các góc khác \({90^0}\), có đúng hai trục đối xứng
-
C.
Hình lục giác đều có đúng 3 trục đối xứng
-
D.
Hình chữ nhật với hai kích thước khác nhau có đúng hai trục đối xứng
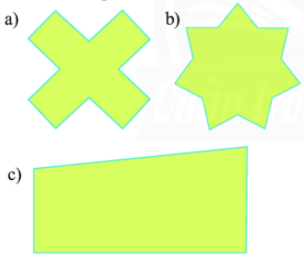
-
A.
hình a
-
B.
hình b
-
C.
hình a và hình b
-
D.
không có hình nào
Tìm \(x\) biết \(9 + x = 2.\)
-
A.
$7$
-
B.
$ - 7$
-
C.
$11$
-
D.
$ - 11$
Phát biểu nào sau đây sai ?
-
A.
Hình lục giác đều có 6 đỉnh
-
B.
Hình lục giác đều có 6 cạnh
-
C.
Hình lục giác đều có 6 đường chéo chính
-
D.
Hình lục giác đều có 6 góc
Tính giá trị biểu thức \(P = {\left( { - 13} \right)^2}.\left( { - 9} \right)\) ta có
-
A.
\(117\)
-
B.
\( - 117\)
-
C.
\(1521\)
-
D.
\( - 1521\)
Cho \(a,b,c\) là các số tự nhiên tùy ý. Khẳng định nào sau đây sai ?
-
A.
\(abc = \left( {ab} \right)c\)
-
B.
\(abc = a\left( {bc} \right)\)
-
C.
\(abc = b\left( {ac} \right)\)
-
D.
\(abc = a + b + c\)
-
A.
EF
-
B.
HG
-
C.
HF
-
D.
FG
Thứ tự thực hiện phép tính nào sau đây là đúng đối với biểu thức không có dấu ngoặc?
-
A.
Cộng và trừ \( \to \) Nhân và chia \( \to \)Lũy thừa
-
B.
Nhân và chia\( \to \)Lũy thừa\( \to \) Cộng và trừ
-
C.
Lũy thừa\( \to \) Nhân và chia \( \to \) Cộng và trừ
-
D.
Cả ba đáp án A,B,C đều đúng

-
A.
\( - 3\) và \( - 5\)
-
B.
\( - 3\) và \( - 2\)
-
C.
\(1\) và \(2\)
-
D.
\( - 5\) và \( - 6\)
\(5125 + 456875\) bằng
-
A.
\(46200\)
-
B.
\(462000\)
-
C.
\(46300\)
-
D.
\(426000\)
+) Tích của một số chẵn các số nguyên âm là một số nguyên ..(1)..
+) Tích của một số lẻ các số nguyên âm là một số nguyên ..(2)..
Từ thích hợp để điền vào hai chỗ chấm trên lần lượt là:
-
A.
âm, dương
-
B.
dương, âm
-
C.
âm, âm
-
D.
dương, dương
Chọn phát biểu sai :
-
A.
Tam giác đều có ba cạnh
-
B.
Ba cạnh của tam giác đều bằng nhau
-
C.
Bốn góc của tam giác đều bằng nhau
-
D.
Tam giác đều có ba đỉnh
Chọn phát biểu sai ?
-
A.
Hình vuông có bốn cạnh bằng nhau
-
B.
Hình vuông có bốn cặp cạnh đối song song
-
C.
Hình vuông có hai đường chéo bằng nhau
-
D.
Hình vuông có bốn góc bằng nhau
Viết tập hợp $A = \{ x|22 < x \le 27\} $ dưới dạng liệt kê các phần tử ta được:
-
A.
\(A = \left\{ {22;23;24;25;26} \right\}\)
-
B.
\(A = \left\{ {22;23;24;25;26;27} \right\}\)
-
C.
\(A = \left\{ {23;24;25;26;27} \right\}\)
-
D.
\(A = \left\{ {23;24;25;26} \right\}\)
Để đánh số trang của một quyển sách dày \(2746\) trang (bắt đầu từ số 1), ta cần dùng bao nhiêu chữ số?
-
A.
\(9875\)
-
B.
\(9876\)
-
C.
\(9877\)
-
D.
\(9878\)
Một căn phòng hình chữ nhật dài $680$cm, rộng $480$cm. Người ta muốn lát kín căn phòng đó bằng gạch hình vuông mà không có viên gạch nào bị cắt xén. Hỏi viên gạch có độ dài lớn nhất là bao nhiêu?
-
A.
$5\,cm$
-
B.
$10\,cm$
-
C.
$20\,cm$
-
D.
$40\,cm$
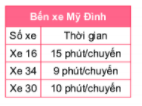
Lịch xuất bến của một số xe buýt tại bến xe Mỹ Đình (Hà Nội) được ghi ở bảng bên. Giả sử các xe buýt xuất bến cùng lúc vào 10 giờ 35 phút. Hỏi vào sau bao lâu thì cả 3 xe xuất bến cùng một lúc lần nữa (kể từ lần đầu tiên)?
-
A.
90 phút
-
B.
45 phút
-
C.
180 phút
-
D.
30 phút
-
A.
\( - {2^o}C\)
-
B.
\({2^o}C\)
-
C.
\( - {10^o}C\)
-
D.
\({10^o}C\)
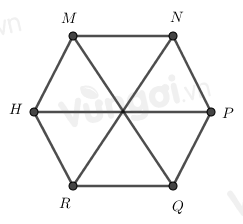
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
-
A.
8
-
B.
2
-
C.
4
-
D.
6
Tính diện tích của hình thoi có tổng độ dài hai đường chéo là 30cm và đường chéo lớn hơn đường chéo bé 2cm.
-
A.
110 cm 2
-
B.
112 cm 2
-
C.
111 cm 2
-
D.
114 cm 2
Bản thiết kế một hiên nhà được biểu thị ở hình sau. Nếu chi phí làm mỗi 9 dm 2 hiên là 103 nghìn đồng thì chi phí của cả hiên nhà sẽ là bao nhiêu?

-
A.
32 445 000 (đồng)
-
B.
34 225 000 (đồng)
-
C.
32 455 000 (đồng)
-
D.
32 544 000 (đồng)
Một hình chữ nhật có chu vi 36 cm và chiều dài gấp đôi chiều rộng thì diện tích của nó bằng bao nhiêu?
-
A.
18 cm 2
-
B.
36 cm 2
-
C.
72 cm 2
-
D.
288 cm 2
-
A.
hình a
-
B.
hình b
-
C.
hình b và hình c
-
D.
hình a và hình b
-
A.
Tam giác đều, trái tim, cánh diều
-
B.
Cánh quạt, trái tim, cánh diều
-
C.
Trái tim, Cánh diều
-
D.
Cả bốn hình

Điền số thích hợp vào ô trống:
\(161291 + \)
\(= (6000 + 725) + 161291\)
Tìm giá trị lớn nhất của biểu thức: \(C = - {\left( {x - 5} \right)^2} + 10\)
-
A.
\( - 10\)
-
B.
\(5\)
-
C.
\(0\)
-
D.
\(10\)
Tìm các giá trị thích hợp của chữ số $a$ sao cho: \( - \overline {a99} > - 649 > - \overline {6a0} \)
-
A.
$6$
-
B.
$5$
-
C.
$4$
-
D.
$7$
Cho \(P = 1 + {5^3} + {5^6} + {5^9} + ... + {5^{99}}\). Chọn đáp án đúng.
-
A.
\(123.P = {5^{102}} - 1\)
-
B.
\(124.P = {5^{102}} - 1\)
-
C.
\(124.P = {5^{101}} - 1\)
-
D.
\(124.P = {5^{102}}\)
Cho 2 số: $14n + 3$ và $21n + 4$ với $n$ là số tự nhiên, chọn đáp án đúng.
-
A.
Hai số trên có hai ước chung
-
B.
Hai số trên có ba ước chung
-
C.
Hai số trên là hai số nguyên tố cùng nhau
-
D.
Hai số trên chỉ có một ước chung là 3.
Cho \(A = 3 + {3^2} + {3^3} + ... + {3^{100}}\) . Tìm số tự nhiên \(n\) biết rằng \(2A + 3 = {3^n}.\)
-
A.
\(n = 99\)
-
B.
\(n = 100\)
-
C.
\(n = 101\)
-
D.
\(n = 102\)
Lời giải và đáp án
Viết tập hợp A các số tự nhiên lớn hơn \(5\) và nhỏ hơn \(10.\)
-
A.
\(A = \left\{ {6;7;8;9} \right\}.\)
-
B.
\(A = \left\{ {5;6;7;8;9} \right\}.\)
-
C.
\(A = \left\{ {6;7;8;9;10} \right\}.\)
-
D.
\(A = \left\{ {6;7;8} \right\}.\)
Đáp án : A
Viết tập hợp \(A\) dưới dạng liệt kê các phần tử thỏa mãn đề bài.
Tập hợp A các số tự nhiên lớn hơn \(5\) và nhỏ hơn \(10\) là \(A = \left\{ {6;7;8;9} \right\}.\)
-
A.
Chiếc bàn có tâm đối xứng
-
B.
Chiếc bàn có trục đối xứng
-
C.
Chiếc bàn vừa có tâm đối xứng và trục đối xứng
-
D.
Chiếc bàn không có tâm đối xứng và trục đối xứng
Đáp án : C
Quan sát hình vẽ ta thấy: Chiếc đĩa vừa có tâm đối xứng và trục đối xứng
Thay dấu * để được số nguyên tố $\overline {3*} $:
-
A.
$7$
-
B.
$4$
-
C.
$6$
-
D.
$9$
Đáp án : A
- Dấu * có thể nhận các giá trị ${\rm{\{ 7; 4; 6; 9\} }}$
- Dùng định nghĩa số nguyên tố để tìm ra số nguyên tố.
Đáp án A: Vì $37$ chỉ chia hết cho \(1\) và \(37\) nên \(37\) là số nguyên tố, do đó chọn A.
Đáp án B: $34$ không phải là số nguyên tố ($34$ chia hết cho $\left\{ {2;{\rm{ }}4;{\rm{ }} \ldots } \right\}$). Do đó loại B.
Đáp án C: $36$ không phải là số nguyên tố ($36$ chia hết cho $\left\{ {1;\,\,2;{\rm{ 3;}}\,...;\,{\rm{36}}} \right\}$). Do đó loại C.
Đáp án D: $39$ không phải là số nguyên tố ($39$ chia hết cho $\left\{ {1;\,\,3;...\,;\,39} \right\}).$ Do đó loại D.
Cho \(\overline {55a62} \) chia hết cho 3. Số thay thế cho \(a\) có thể là
-
A.
1
-
B.
2
-
C.
3
-
D.
5
Đáp án : C
Tìm điều kiện của \(a\) .
Tính tổng các chữ số trong \(\overline {55a62} \)
Tìm \(a\) để tổng đó chia hết cho 3.
Tổng các chữ số của \(\overline {55a62} \) là \(5 + 5 + a + 6 + 2 = a + 18\) để số \(\overline {55a62} \) chia hết cho 3 thì \(a + 18\) phải chia hết cho 3.
Do a là các số tự nhiên từ 0 đến 9 nên
\(\begin{array}{l}0 + 18 \le a + 18 \le 9 + 18\\ \Rightarrow 18 \le a + 18 \le 27\end{array}\)
Số chia hết cho 3 từ 18 đến 27 có thể là các số: 18, 21, 24, 27
Tức là \(a + 18\) có thể nhận các giá trị: 18, 21, 24, 27
Với \(a + 18\) bằng 18 thì \(a = 18 - 18 = 0\)
Với \(a + 18\) bằng 21 thì \(a = 21 - 18 = 3\)
Với \(a + 18\) bằng 24 thì \(a = 24 - 18 = 6\)
Với \(a + 18\) bằng 27 thì \(a = 27 - 18 = 9\)
Vậy số có thể thay thế cho a là một trong các số 0;3;6;9.
Vậy số thay thế cho a trong đề bài chỉ có thể là 3
Cho tổng \(M = 75 + 120 + x\) . Với giá trị nào của \(x\) dưới đây thì \(M \, \vdots \, 3?\)
-
A.
$7$
-
B.
$5$
-
C.
$4$
-
D.
$12$
Đáp án : D
Sử dụng tính chất 1: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó. \(a\, \vdots \,m;\,b\, \vdots \,m;\,c\, \vdots \,m \Rightarrow \left( {a + b + c} \right) \vdots \,m\)
Vì \(75\, \vdots \,3;\,120\, \vdots \,3\) nên để \(M = 75 + 120 + x\) chia hết cho \(3\) thì \(x\, \vdots \,3\) nên ta chọn \(x = 12.\)
Cho n là một số tự nhiên lớn hơn 2 và nhỏ hơn 5. Khẳng định nào sau đây đúng ?
-
A.
n nằm bên phải điểm 5 trên tia số
-
B.
n nằm bên trái điểm 2 trên tia số
-
C.
n nằm bên phải điểm 2 trên tia số
-
D.
n nằm bên phải điểm 5 và cách điểm 5 một đơn vị trên tia số.
Đáp án : C
+ Vẽ tia số.
+ Số tự nhiên lớn hơn thì nằm bên phải, nhỏ hơn thì nằm bên trái.
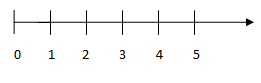
n là một số tự nhiên lớn hơn 2 nên n nằm bên phải điểm 2 => B sai, C đúng
n là một số tự nhiên nhỏ hơn 5 nên n nằm bên trái điểm 2 =>A,D sai.
Cho tam giác đều \(MNP\) có \(MN = 5\,cm\), khẳng định nào sau đây đúng?
-
A.
\(NP = 3\,cm\)
-
B.
\(MP = 4\,cm\)
-
C.
\(NP = 6\,cm\)
-
D.
\(MP = 5\,cm\)
Đáp án : D
Trong tam giác đều ba cạnh bằng nhau mà \(MN = 5\,cm\) nên ta có: \(MN = NP = MP = 5\,cm\)
=> Chọn D
$BCNN(9;24)$ là bao nhiêu?
-
A.
$54$
-
B.
$18$
-
C.
$72$
-
D.
$36$
Đáp án : C
Bước 1 : Phân tích mỗi số ra thừa số nguyên tố.
Bước 2 : Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3 : Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
Ta có:
$\begin{array}{l}9 = {3^2};24 = {2^3}.3\\ \Rightarrow BCNN\left( {9;24} \right) = {2^3}{.3^2} = 8.9 = 72\end{array}$
Trong các số sau, số nào vừa chia hết cho 2 vừa chia hết cho 5?
-
A.
550
-
B.
9724
-
C.
7905
-
D.
5628
Đáp án : A
Sử dụng dấu hiệu chia hết cho 2: Các số có chữ số tận cùng là 0,2,4,6,8 thì chia hết cho 2 và chỉ những số đó chia hết cho 2.
Dấu hiệu chia hết cho 5: Các chữ số có tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó chia hết cho 5.
Tìm số thỏa mãn cả 2 dấu hiệu trên.
550 có chữ số tận cùng là 0.
Số có chữ số tận cùng là 0 thì chia hết cho 2 và chia hết cho 5.
Vậy 550 vừa chia hết cho 2 vừa chia hết cho 5
Cho \(x - 236\) là số đối của số 0 thì x là:
-
A.
\( - 234\)
-
B.
\(234\)
-
C.
\(0\)
-
D.
\(236\)
Đáp án : D
+ Số đối của 0 là 0.
+ Áp dụng quy tắc chuyển vế, quy tắc cộng hai số nguyên cùng dấu để tìm x.
Số đối của số 0 là 0.
Vì \(x - 236\) là số đối của số 0 nên
\(\begin{array}{l}x - 236 = 0\\x\;\;\;\;\;\;\;\;\; = 0 + 236\\x\;\;\;\;\;\;\;\;\; = 236.\end{array}\)
Trong các câu sau câu nào sai:
-
A.
Hình vuông có đúng 4 trục đối xứng
-
B.
Hình thoi, các góc khác \({90^0}\), có đúng hai trục đối xứng
-
C.
Hình lục giác đều có đúng 3 trục đối xứng
-
D.
Hình chữ nhật với hai kích thước khác nhau có đúng hai trục đối xứng
Đáp án : C
Các câu A, B, D đúng.
Hình lục giác đều có 6 trục đối xứng gồm 3 đường thẳng đi qua hai định đổi diện và 3 đường thẳng đi qua trung điểm của hai cạnh đối diện => C sai.
-
A.
hình a
-
B.
hình b
-
C.
hình a và hình b
-
D.
không có hình nào
Đáp án : A
Hình a có trục đối xứng.
Tìm \(x\) biết \(9 + x = 2.\)
-
A.
$7$
-
B.
$ - 7$
-
C.
$11$
-
D.
$ - 11$
Đáp án : B
Muốn tìm số hạng chưa biết trong một tổng, ta thực hiện: Số hạng chưa biết $ = $ Tổng $ - $ Số hạng đã biết
\(\begin{array}{l}9 + x = 2\\x = 2 - 9\\x = - 7\end{array}\)
Phát biểu nào sau đây sai ?
-
A.
Hình lục giác đều có 6 đỉnh
-
B.
Hình lục giác đều có 6 cạnh
-
C.
Hình lục giác đều có 6 đường chéo chính
-
D.
Hình lục giác đều có 6 góc
Đáp án : C
Sử dụng dấu hiệu nhận biết lục giác đều.
Các đáp án A, B, D đúng.
Hình lục giác đều có 3 đường chéo chính => Đáp án C sai .
Tính giá trị biểu thức \(P = {\left( { - 13} \right)^2}.\left( { - 9} \right)\) ta có
-
A.
\(117\)
-
B.
\( - 117\)
-
C.
\(1521\)
-
D.
\( - 1521\)
Đáp án : D
Thứ tự thực hiện phép tính: Bình phương trước rồi thực hiện phép nhân hai số nguyên.
\(P = {\left( { - 13} \right)^2}.\left( { - 9} \right) = 169.\left( { - 9} \right) = - 1521\)
Cho \(a,b,c\) là các số tự nhiên tùy ý. Khẳng định nào sau đây sai ?
-
A.
\(abc = \left( {ab} \right)c\)
-
B.
\(abc = a\left( {bc} \right)\)
-
C.
\(abc = b\left( {ac} \right)\)
-
D.
\(abc = a + b + c\)
Đáp án : D
Tích \(\left( {ab} \right)c\) hay \(a\left( {bc} \right)\) gọi là tích cả ba số a, b, c và viết gọn là \(abc\) .
Tính chất giao hoán: \(a.b = b.a\)
\(\begin{array}{l}\left( {ab} \right)c = \left( {a.b} \right).c = a.b.c = abc\\a\left( {bc} \right) = a.\left( {b.c} \right) = a.b.c = abc\\b\left( {ac} \right) = b.\left( {a.c} \right) = b.a.c = a.b.c = abc\end{array}\)
-
A.
EF
-
B.
HG
-
C.
HF
-
D.
FG
Đáp án : D
Sử dụng: Trong hình thang cân hai cạnh bên bằng nhau.
Do góc EH và FG là cạnh bên của hình thang EFGH nên:
\(EH=FG\)
Thứ tự thực hiện phép tính nào sau đây là đúng đối với biểu thức không có dấu ngoặc?
-
A.
Cộng và trừ \( \to \) Nhân và chia \( \to \)Lũy thừa
-
B.
Nhân và chia\( \to \)Lũy thừa\( \to \) Cộng và trừ
-
C.
Lũy thừa\( \to \) Nhân và chia \( \to \) Cộng và trừ
-
D.
Cả ba đáp án A,B,C đều đúng
Đáp án : C
Đối với biểu thức không có dấu ngoặc thì thứ tự thực hiện phép tính đúng là : Lũy thừa\( \to \) Nhân và chia \( \to \) Cộng và trừ

-
A.
\( - 3\) và \( - 5\)
-
B.
\( - 3\) và \( - 2\)
-
C.
\(1\) và \(2\)
-
D.
\( - 5\) và \( - 6\)
Đáp án : B
\(5125 + 456875\) bằng
-
A.
\(46200\)
-
B.
\(462000\)
-
C.
\(46300\)
-
D.
\(426000\)
Đáp án : B
Đặt tính rồi tính.

Vậy \(5125 + 456875 = 462000\)
+) Tích của một số chẵn các số nguyên âm là một số nguyên ..(1)..
+) Tích của một số lẻ các số nguyên âm là một số nguyên ..(2)..
Từ thích hợp để điền vào hai chỗ chấm trên lần lượt là:
-
A.
âm, dương
-
B.
dương, âm
-
C.
âm, âm
-
D.
dương, dương
Đáp án : B
- Tích của hai số nguyên trái dấu là số nguyên âm.
- Tính của hai số nguyên cùng dấu là số nguyên dương.
+) Tích của một số chẵn các số nguyên âm là một số nguyên dương
+) Tích của một số lẻ các số nguyên âm là một số nguyên âm
Chọn phát biểu sai :
-
A.
Tam giác đều có ba cạnh
-
B.
Ba cạnh của tam giác đều bằng nhau
-
C.
Bốn góc của tam giác đều bằng nhau
-
D.
Tam giác đều có ba đỉnh
Đáp án : C
Trong tam giác đều ba góc bằng nhau => Đáp án C sai.
Chọn phát biểu sai ?
-
A.
Hình vuông có bốn cạnh bằng nhau
-
B.
Hình vuông có bốn cặp cạnh đối song song
-
C.
Hình vuông có hai đường chéo bằng nhau
-
D.
Hình vuông có bốn góc bằng nhau
Đáp án : B
Sử dụng dấu hiệu nhận biết của hình vuông.
Hình vuông có hai cặp cạnh đối song song => Đáp án B sai.
Viết tập hợp $A = \{ x|22 < x \le 27\} $ dưới dạng liệt kê các phần tử ta được:
-
A.
\(A = \left\{ {22;23;24;25;26} \right\}\)
-
B.
\(A = \left\{ {22;23;24;25;26;27} \right\}\)
-
C.
\(A = \left\{ {23;24;25;26;27} \right\}\)
-
D.
\(A = \left\{ {23;24;25;26} \right\}\)
Đáp án : C
+ Chỉ ra các số lớn hơn \(22\) và nhỏ hơn hoặc bằng \(27.\)
+ Từ đó viết tập hợp A dưới dạng liệt kê.
Các số lớn hơn \(22\) và nhỏ hơn hoặc bằng \(27\) là \(23;24;25;26;27.\)
Nên \(A = \left\{ {23;24;25;26;27} \right\}.\)
Để đánh số trang của một quyển sách dày \(2746\) trang (bắt đầu từ số 1), ta cần dùng bao nhiêu chữ số?
-
A.
\(9875\)
-
B.
\(9876\)
-
C.
\(9877\)
-
D.
\(9878\)
Đáp án : C
+ Tìm số trang có đánh 1 chữ số, số trang đánh 2 chữ số, số trang đánh 3 chữ số, số trang đánh 4 chữ số
+ Từ đó suy ra số chữ số cần dùng.
Quyển sách có:
+ Số trang có \(1\) chữ số là \(9 - 1 + 1 = 9\)
+ Số trang có \(2\) chữ số là \(99 - 10 + 1 = 90\) trang
+ Số trang có \(3\) chữ số là \(999 - 100 + 1 = 900\) trang
+ Số trang có \(4\) chữ số là \(2746 - 1000 + 1 = 1747\) trang
Vậy số chữ số cần dùng là:
\(1.9 + 2.90 + 3.900 + 4.1747 = 9877\) (chữ số)
Một căn phòng hình chữ nhật dài $680$cm, rộng $480$cm. Người ta muốn lát kín căn phòng đó bằng gạch hình vuông mà không có viên gạch nào bị cắt xén. Hỏi viên gạch có độ dài lớn nhất là bao nhiêu?
-
A.
$5\,cm$
-
B.
$10\,cm$
-
C.
$20\,cm$
-
D.
$40\,cm$
Đáp án : D
Vì muốn lát gạch kín căn phòng mà không có viên gạch nào bị cắt xén thì độ dài cạnh viên gạch phải là ước của $680$ và $480.$ Để viên gạch có độ dài lớn nhất thì đồ dài cạnh viên gạch bằng ƯCLN$\left( {680;480} \right).$
Ta có: Gọi chiều dài viên gạch là $x.$ Để lát kín căn phòng mà không có có viên gạch nào bị cắt xén thì $x$ phải là ước của chiều dài và chiều rộng căn phòng Hay $680 \, \vdots \, x$ và $480 \, \vdots \, x$ $ \Rightarrow x \in $ ƯC$\left( {680;480} \right)$ Để x là lớn nhất $ \Rightarrow x = $ƯCLN$\left( {680;480} \right)$ Ta có: $680 = {2^3}.5.17;$ $480 = {2^5}.3.5$ $ \Rightarrow x = $ ƯCLN$\left( {680;480} \right)$$ = {2^3}.5 = 40$ Vậy để lát kín căn phòng mà không có viên gạch nào bị cắt xén thì độ dài cạnh viên gạch lớn nhất là $40$ $cm.$
Lịch xuất bến của một số xe buýt tại bến xe Mỹ Đình (Hà Nội) được ghi ở bảng bên. Giả sử các xe buýt xuất bến cùng lúc vào 10 giờ 35 phút. Hỏi vào sau bao lâu thì cả 3 xe xuất bến cùng một lúc lần nữa (kể từ lần đầu tiên)?

-
A.
90 phút
-
B.
45 phút
-
C.
180 phút
-
D.
30 phút
Đáp án : A
- Tính xem cứ bao nhiêu phút thì các xe xuất bến cùng lúc: BCNN(15, 9, 10)
Thời gian các xe cùng xuất bến cách 10h35p các khoảng thời gian là BC(9, 10, 15)
Ta có: 9 = \({3^2}\), 10 = 2.5, 15 = 3.5.
Thừa số chung và riêng là 2, 3 và 5
Số mũ lớn nhất của 2 là 1
Số mũ lớn nhất của 3 là 2
Số mũ lớn nhất của 5 là 1
=> BCNN(9, 10, 15) = \({2.3^2}.5\) = 90
Vậy cứ 90 phút thì các xe xuất bến cùng một lúc.
-
A.
\( - {2^o}C\)
-
B.
\({2^o}C\)
-
C.
\( - {10^o}C\)
-
D.
\({10^o}C\)
Đáp án : B
- Nhiệt độ 10h = ( Nhiệt độ lúc 7h ) + \(6^\circ C\).
- Sử dụng quy tắc cộng hai số nguyên khác dấu.
Nhiệt độ ở Ôt-ta-oa lúc 10 giờ là:
\(\left( { - 4} \right) + 6 = 6 - 4 = 2\left( {^\circ C} \right)\)
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều

-
A.
8
-
B.
2
-
C.
4
-
D.
6
Đáp án : D
Đếm số tam giác đều đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
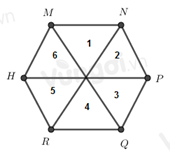
Ta đánh số như hình trên
Nhận thấy có các hình tam giác đều là: 1, 2, 3, 4, 5, 6.
Vậy có 6 tam giác đều.
Tính diện tích của hình thoi có tổng độ dài hai đường chéo là 30cm và đường chéo lớn hơn đường chéo bé 2cm.
-
A.
110 cm 2
-
B.
112 cm 2
-
C.
111 cm 2
-
D.
114 cm 2
Đáp án : B
- Độ dài đường chéo lớn = (Tổng độ dài hai đường chéo + Hiệu độ dài hai đường chéo) : 2
=> Độ dài đường chéo bé = Tổng độ dài hai đường chéo - Độ dài đường chéo lớn
- Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\).
Độ dài đường chéo lớn là: \(\left( {30 + 2} \right):2 = 16\,\left( {cm} \right)\)
Độ dài đường chéo bé là: \(30 - 16 = 14\left( {cm} \right)\)
Diện tích hình thoi là: \(\frac{{16.14}}{2} = 112\left( {c{m^2}} \right)\)
Bản thiết kế một hiên nhà được biểu thị ở hình sau. Nếu chi phí làm mỗi 9 dm 2 hiên là 103 nghìn đồng thì chi phí của cả hiên nhà sẽ là bao nhiêu?

-
A.
32 445 000 (đồng)
-
B.
34 225 000 (đồng)
-
C.
32 455 000 (đồng)
-
D.
32 544 000 (đồng)
Đáp án : A
Diện tích hình hình thang = \(\frac{1}{2}\). Chiều cao.(đáy lớn + đáy nhỏ).
Chi phí = Diện tích hình thang : 9 . 103 000
Diện tích của hiên nhà là: \(\frac{1}{2}\).45.(54 + 72) = 2835 (dm 2 )
Vậy chi phí của cả hiên là: 2835 : 9 . 103 000 = 32 445 000 (đồng).
Một hình chữ nhật có chu vi 36 cm và chiều dài gấp đôi chiều rộng thì diện tích của nó bằng bao nhiêu?
-
A.
18 cm 2
-
B.
36 cm 2
-
C.
72 cm 2
-
D.
288 cm 2
Đáp án : C
- Tính nửa chu vi HCN
- Tính chiều dài và chiều rộng hình chữ nhật (Đưa về bài toán tìm hai số khi biết tổng và tỉ số của chúng).
- Tính diện tích HCN
Nửa chu vi hình chữ nhật là:
\(36:2 = 18\,\left( {cm} \right)\)
Chiều dài hình chữ nhật là:
\(18:\left( {2 + 1} \right).2 = 12\left( {cm} \right)\)
Chiều rộng hình chữ nhật là:
\(18 - 12 = 6\,\left( {cm} \right)\)
Diện tích hình chữ nhật là:
\(12.6 = 72\,\,(c{m^2})\)
-
A.
hình a
-
B.
hình b
-
C.
hình b và hình c
-
D.
hình a và hình b
Đáp án : D
Hình a và hình b có trục đối xứng, ví dụ ta có thể vẽ trục đối xứng của chúng như sau:

-
A.
Tam giác đều, trái tim, cánh diều
-
B.
Cánh quạt, trái tim, cánh diều
-
C.
Trái tim, Cánh diều
-
D.
Cả bốn hình
Đáp án : D
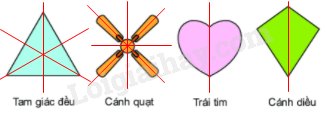
Những hình có trục đối xứng: tam giác đều, cánh quạt, trái tim, cánh diều.

Điền số thích hợp vào ô trống:
\(161291 + \)
\(= (6000 + 725) + 161291\)
\(161291 + \)
\(= (6000 + 725) + 161291\)
Áp dụng tính chất giao hoán của phép cộng: Khi đổi chỗ các số hạng trong một tổng thì tổng đó không thay đổi.
Ta có: \((6000 + 725) + 161291 = 6725 + 161291\)
Hay \(161291 + 6725 = (6000 + 725) + 161291\)
Vậy đáp án đúng điền vào ô trống là \(6725\).
Tìm giá trị lớn nhất của biểu thức: \(C = - {\left( {x - 5} \right)^2} + 10\)
-
A.
\( - 10\)
-
B.
\(5\)
-
C.
\(0\)
-
D.
\(10\)
Đáp án : D
Áp dụng tính chất \({A^2} \ge 0\) với mọi A và tính chất \(m - {A^2} \le m\) để tìm giá trị lớn nhất của biểu thức.
\(C = - {\left( {x - 5} \right)^2} + 10\)
Ta có: \({\left( {x - 5} \right)^2} \ge 0,\,\forall x \in \mathbb{Z} \Rightarrow - {\left( {x - 5} \right)^2} \le 0,\;\,\forall x \in \mathbb{Z}\)\( \Rightarrow - {\left( {x - 5} \right)^2} + 10 \le 10,\,\;\forall x \in \mathbb{Z}\)
Suy ra \(C \le 10\,\,\forall x \in \mathbb{Z}\) .
\(C = 10\) khi \({\left( {x - 5} \right)^2} = 0 \Rightarrow x - 5 = 0 \Rightarrow x = 5\)
Vậy giá trị lớn nhất của C là 10 khi \(x = 5\) .
Tìm các giá trị thích hợp của chữ số $a$ sao cho: \( - \overline {a99} > - 649 > - \overline {6a0} \)
-
A.
$6$
-
B.
$5$
-
C.
$4$
-
D.
$7$
Đáp án : B
Dựa vào việc so sánh hai số nguyên:
+ Với \(a,b \in Z\), nếu điểm $a$ nằm bên trái điểm $b$ trên trục số nằm ngang thì \(a < b\)
+ Số nguyên $b$ là số liền sau của số nguyên $a$ nếu \(a < b\) và giữa $a$ và $b$ không có số nguyên nào nữa.
\( - \overline {a99} > - 649 > - \overline {6a0} \Rightarrow \overline {a99} < 649 < \overline {6a0} \Rightarrow \left\{ \begin{array}{l}a < 6\\4 < a\end{array} \right. \Rightarrow 4 < a < 6\).
Mà \(a \in {N^*}\) nên \(a = 5\).
Cho \(P = 1 + {5^3} + {5^6} + {5^9} + ... + {5^{99}}\). Chọn đáp án đúng.
-
A.
\(123.P = {5^{102}} - 1\)
-
B.
\(124.P = {5^{102}} - 1\)
-
C.
\(124.P = {5^{101}} - 1\)
-
D.
\(124.P = {5^{102}}\)
Đáp án : B
Nhân thêm vào hai vế của biểu thức $P$ với \({5^3}\) để được biểu thức mới, sau đó lấy biểu thức mới trừ đi biểu thức ban đầu, biến đổi để được biểu thức rút gọn của $P$.
\(\begin{array}{l}P = 1 + {5^3} + {5^6} + {5^9} + ... + {5^{99}}\\{5^3}.P = {5^3}.\left( {1 + {5^3} + {5^6} + {5^9} + ... + {5^{99}}} \right) = {5^3} + {5^6} + {5^9} + ... + {5^{99}} + {5^{102}}\\125.P = {5^3} + {5^6} + {5^9} + ... + {5^{99}} + {5^{102}}\\ \Rightarrow 125.P - P = \left( {{5^3} + {5^6} + {5^9} + ... + {5^{99}} + {5^{102}}} \right) - \left( {1 + {5^3} + {5^6} + {5^9} + ... + {5^{99}}} \right)\\ \Rightarrow 124.P = {5^{102}} - 1\end{array}\)
Cho 2 số: $14n + 3$ và $21n + 4$ với $n$ là số tự nhiên, chọn đáp án đúng.
-
A.
Hai số trên có hai ước chung
-
B.
Hai số trên có ba ước chung
-
C.
Hai số trên là hai số nguyên tố cùng nhau
-
D.
Hai số trên chỉ có một ước chung là 3.
Đáp án : C
Dựa vào kiến thức 2 số nguyên tố cùng nhau là 2 số nguyên tố có ước chung lớn nhất là 1.
Áp dụng tính chất chia hết của 1 hiệu: Nếu $a \vdots c;b \vdots c \Rightarrow \left( {a - b} \right) \vdots c$
Gọi \(d = UCLN\left( {14n + 3;21n + 4} \right)\) ta có:
\(14n + 3\, \vdots \,d\) và \(21n + 4 \, \vdots \, d\)
\(3\left( {14n + 3} \right) \vdots \, d\) và \(2\left( {21n + 4} \right) \vdots d\)
\(42n + 9 \,\vdots \, d\) và \(42n + 8 \, \vdots \, d\)
\(\left( {42n + 9} \right) - \left( {42n + 8} \right) \vdots d\)
Suy ra \(1 \vdots d\)
\(d = 1\)
Vậy \(ƯCLN\left( {14n + 3;21n + 4} \right) = 1\) hay hai số đó là hai số nguyên tố cùng nhau.
Cho \(A = 3 + {3^2} + {3^3} + ... + {3^{100}}\) . Tìm số tự nhiên \(n\) biết rằng \(2A + 3 = {3^n}.\)
-
A.
\(n = 99\)
-
B.
\(n = 100\)
-
C.
\(n = 101\)
-
D.
\(n = 102\)
Đáp án : C
+ Tính \(3A\) sau đó tính \(2A = 3A - A\)
+ Sử dụng điều kiện ở đề bài để đưa về dạng hai lũy thừa cùng cơ số. Cho hai số mũ bằng nhau ta tìm được \(n.\)
Ta có \(A = 3 + {3^2} + {3^3} + ... + {3^{100}}\,\,\left( 1 \right)\) nên \(3A = {3^2} + {3^3} + {3^4} + ... + {3^{100}} + {3^{101}}\,\,\left( 2 \right)\)
Lấy \(\left( 2 \right)\) trừ \(\left( 1 \right)\) ta được \(2A = {3^{101}} - 3\) do đó \(2A + 3 = {3^{101}}\) mà theo đề bài \(2A + 3 = {3^n}\)
Suy ra \({3^n} = {3^{101}}\) nên \(n = 101.\)