Đề kiểm tra giữa học kì 1 Toán 6 Kết nối tri thức - Đề số 4
Đề bài

Các số không chia hết cho \(5\) có chữ số tận cùng là:
A. \(1\,;\,\,2\,;\,\,3\,;\,\,4\)
B. \(6\,;\,\,7\)
C. \(8\,;\,\,9\)
D. Tất cả các đáp án trên đều đúng
Tìm chu vi hình tam giác ABC có ba cạnh bằng nhau, biết cạnh AC = 5 cm.
-
A.
15 dm
-
B.
10 cm
-
C.
15 cm
-
D.
20 cm
Chọn phát biểu sai ?
-
A.
Hình vuông có bốn cạnh bằng nhau
-
B.
Hình vuông có bốn cặp cạnh đối song song
-
C.
Hình vuông có hai đường chéo bằng nhau
-
D.
Hình vuông có bốn góc bằng nhau
Khi phân tích các số \(2150;1490;2340\) ra thừa số nguyên tố thì số nào có chứa tất cả các thừa số nguyên tố \(2;3\) và \(5?\)
-
A.
$2340$
-
B.
$2150$
-
C.
$1490$
-
D.
Cả ba số trên.
Cho tổng A = 12 + 14 + 16 + x; x là số tự nhiên. Để A không chia hết cho 2 thì
-
A.
\(x = 199\)
-
B.
\(x = 198\)
-
C.
\(x = 1000\)
-
D.
\(x = 50054\)
 Điền số hoặc chữ thích hợp vào ô trống:
Điền số hoặc chữ thích hợp vào ô trống:
\(a + b + 91 = (a + b) +\)
\(=\)
\(+ (b + 91)\)
Cho hình vuông ABCD có chu vi bằng 28cm. Diện tích hình vuông ABCD là:
-
A.
\(49\,cm\)
-
B.
\(28\,c{m^2}\)
-
C.
\(49\,c{m^2}\)
-
D.
\(112\,c{m^2}\)
Tìm BCNN(4, 7).
-
A.
24
-
B.
21
-
C.
28
-
D.
0

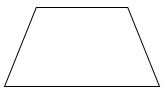
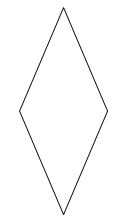
Trong các hình sau, hình nào là hình thoi?
A.
B.
C.

D.

Chọn câu đúng:
-
A.
Chu vi của một hình bình hành bằng tổng một cặp cạnh kề nhau bất kỳ.
-
B.
Chu vi hình bình hành bằng tổng của cạnh đáy và chiều cao.
-
C.
Chu vi hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
-
D.
Chu vi của một hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.
Số $x$ là bội chung của ${\rm{a;b;c}}$ nếu:
-
A.
$x \, \vdots \, a$ hoặc $x \, \vdots \, b$ hoặc $x \, \vdots \, c$
-
B.
$x \, \vdots \, a$ và $x \, \vdots \, b$
-
C.
$x \, \vdots \, b$ và $x \, \vdots \, c$
-
D.
$x \, \vdots \, a$ và $x \, \vdots \, b$ và $x \, \vdots \, c$
Diện tích hình thoi có độ dài hai đường chéo là 15cm và 6cm là:
-
A.
90 cm 2
-
B.
45 dm 2
-
C.
45 cm 2
-
D.
50 cm 2
Viết tập hợp A các số tự nhiên lớn hơn \(5\) và nhỏ hơn \(10.\)
-
A.
\(A = \left\{ {6;7;8;9} \right\}.\)
-
B.
\(A = \left\{ {5;6;7;8;9} \right\}.\)
-
C.
\(A = \left\{ {6;7;8;9;10} \right\}.\)
-
D.
\(A = \left\{ {6;7;8} \right\}.\)
Cho phép tính \(231 - 87\). Chọn câu đúng.
-
A.
\(231\) là số trừ
-
B.
\(87\) là số bị trừ
-
C.
\(231\) là số bị trừ
-
D.
\(87\) là hiệu
Với ba chữ số \(0;1;3\) có thể viết được bao nhiêu số có ba chữ số khác nhau?
-
A.
\(4\)
-
B.
\(3\)
-
C.
\(5\)
-
D.
\(6\)
Thứ tự thực hiện phép tính nào sau đây là đúng đối với biểu thức có dấu ngoặc?
-
A.
\(\left[ {} \right] \to \left( {} \right) \to \left\{ {} \right\}\)
-
B.
\(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
-
C.
\(\left\{ {} \right\} \to \left[ {} \right] \to \left( {} \right)\)
-
D.
\(\left[ {} \right] \to \left\{ {} \right\} \to \left( {} \right)\)
Khẳng định nào sau đây sai ?
-
A.
\(a + b + c = \left( {a + b} \right) + c\)
-
B.
\(a + b + c = \left( {a + c} \right) + b\)
-
C.
\(a + b + c = \left( {a + b} \right) + b\)
-
D.
\(a + b + c = a + \left( {b + c} \right)\)
Trong những khẳng định sau, khẳng định nào sai ?
-
A.
Hình bình hành có 4 đỉnh
-
B.
Hình bình hành có bốn cạnh
-
C.
Hình có bốn đỉnh là hình bình hành
-
D.
Hình bình hành có hai cạnh đối song song.
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
Phép toán \({6^2}:4.3 + {2.5^2}\) có kết quả là:
-
A.
$77$
-
B.
$78$
-
C.
$79$
-
D.
$80$
Tìm số tự nhiên $x$ thỏa mãn: $7+x=362$.
-
A.
300
-
B.
355
-
C.
305
-
D.
362
-
A.
\(BC\, = 5\,cm\)
-
B.
\(AC = 5\,cm\)
-
C.
\(AD = \,5\,cm\)
-
D.
\(DC = 5\,cm\)
Cho \(\overline {1a52} \) chia hết cho 9. Số thay thế cho \(a\) có thể là
-
A.
1
-
B.
2
-
C.
3
-
D.
5
Các số có chữ số tận cùng là … thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
-
A.
0, 1, 2, 3
-
B.
0, 2, 4, 6, 8
-
C.
1, 3, 5, 7, 9
-
D.
0 hoặc 5
Kết quả của phép tính $12.100 + 100.36 - 100.19$ là
-
A.
\(29000\)
-
B.
\(3800\)
-
C.
\(290\)
-
D.
\(2900\)
Cho hình vẽ như sau:
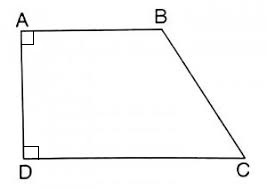
Cạnh AB song song với cạnh nào dưới đây?
A. BC
B. DC
C. AD
-
A.
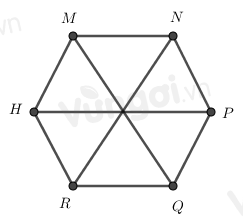
6 đỉnh là M, N, P, Q, R, H
-
B.
6 cạnh là MN, NP, PQ, MQ, QR, HM
-
C.
3 đường chéo chính là MQ, HP, RN.
-
D.
3 đường chéo chính cắt nhau tại 1 điểm.
Không tính giá trị cụ thể, hãy so sánh \(A = 1987657.1987655\) và \(B = 1987656.1987656\)
-
A.
\(A > B\)
-
B.
\(A < B\)
-
C.
\(A \le B\)
-
D.
\(A = B\)
Tìm số tự nhiên \(x\) biết rằng \(x - 50:25 = 8.\)
-
A.
\(11\)
-
B.
\(250\)
-
C.
\(10\)
-
D.
\(20\)
Tính giá trị của biểu thức \(A = \dfrac{{{{11.3}^{22}}{{.3}^7} - {9^{15}}}}{{{{\left( {{{2.3}^{13}}} \right)}^2}}}\)
-
A.
\(A = 18\)
-
B.
\(A = 9\)
-
C.
\(A = 54.\)
-
D.
\(A = 6\)
Có bao nhiêu số tự nhiên \(n\) để \( (n + 4) \, \vdots \, n\) ?
-
A.
\(3\)
-
B.
\(4\)
-
C.
\(2\)
-
D.
\(1\)

Từ ba chữ số $2\,;\,\,5\,;\,\,8{\rm{ }}$ hãy viết các số có hai chữ số khác nhau và chia hết cho \(5\).
A. \(28\,;\,\,58\)
B.\(\,25;\,\,85\)
C. \(25\,\, ;\,\,\,58\,\)
D. \(25\,;\,55\,;\,85\,\)
Tìm các chữ số $x, y$ biết rằng: \(\overline {23x5y} \) chia hết cho $2; 5$ và $9.$
-
A.
\(x = 0;y = 6\)
-
B.
\(x = 6;y = 0\)
-
C.
\(x = 8;y = 0\)
-
D.
\(x = 0;y = 8\)
Một hình vuông có diện tích là \(1936\,{m^2}.\) Tính cạnh của hình vuông đó.
-
A.
$44$
-
B.
$46$
-
C.
$22$
-
D.
$48$
Tìm \(x\) biết $120$ $ \vdots $ $x$; $200$ $ \vdots $ $x$ và \(x < 40\)
-
A.
\(x \in \left\{ {1;2;4;5;8;10;20} \right\}\)
-
B.
\(x \in \left\{ {2;5;10;20;40} \right\}\)
-
C.
\(x \in \left\{ {1;2;5;10;20;40} \right\}\)
-
D.
\(x \in \left\{ {2;5;10;20} \right\}\)
Tính diện tích của hình thoi có tổng độ dài hai đường chéo là 30cm và đường chéo lớn hơn đường chéo bé 2cm.
-
A.
110 cm 2
-
B.
112 cm 2
-
C.
111 cm 2
-
D.
114 cm 2
Để đánh số các trang của một quyển sách người ta phải dùng tất cả \(600\) chữ số. Hỏi quyển sách có bao nhiêu trang?
-
A.
\(326\)
-
B.
\(136\)
-
C.
\(263\)
-
D.
\(236\)
 Tìm \(x\) biết: \(45 + (1234 + x) = 1234 + (45 + 120)\)
Tìm \(x\) biết: \(45 + (1234 + x) = 1234 + (45 + 120)\)
A. \(x = 120\)
B. \(x = 125\)
C. \(x = 145\)
D. \(x = 165\)

Điền số thích hợp vào ô trống:
Từ bốn chữ số $0;{\rm{ 3; 5;}}\,\,9$ có thể viết được
số có ba chữ số khác nhau và chia hết cho \(5\).
Sân trường em hình vuông. Để tăng thêm diện tích nhà trường mở rộng về mỗi phía 4m thì diện tích tăng thêm 192m 2 . Hỏi trước đây sân trường em có diện tích là bao nhiêu m 2 ?
-
A.
16 m 2
-
B.
32 m 2
-
C.
64 m 2
-
D.
128 m 2
Lời giải và đáp án

Các số không chia hết cho \(5\) có chữ số tận cùng là:
A. \(1\,;\,\,2\,;\,\,3\,;\,\,4\)
B. \(6\,;\,\,7\)
C. \(8\,;\,\,9\)
D. Tất cả các đáp án trên đều đúng
D. Tất cả các đáp án trên đều đúng
Các số không có chữ số tận cùng là \(0\) hoặc \(5\) thì không chia hết cho \(5\).
Do đó các số không chia hết cho \(5\) có chữ số tận cùng là \(1\,;\,\,2\,;\,\,3\,;\,\,4;\,\,6\,;\,\,7\,;\,\,8\,;\,\,9\).
Vậy tất cả các đáp án A, B, C đều đúng.
Tìm chu vi hình tam giác ABC có ba cạnh bằng nhau, biết cạnh AC = 5 cm.
-
A.
15 dm
-
B.
10 cm
-
C.
15 cm
-
D.
20 cm
Đáp án : C
Chu vi của một hình tam giác bằng tổng độ dài 3 cạnh.
Do hình tam giác ABC có bốn cạnh bằng nhau và AC = 5 cm nên :
Chu vi tam giác ABC là: \(5 + 5 + 5 = 15\)(cm)
Cách khác:
Chu vi tam giác ABC là: \(5.3 = 15\) (cm).
Chọn phát biểu sai ?
-
A.
Hình vuông có bốn cạnh bằng nhau
-
B.
Hình vuông có bốn cặp cạnh đối song song
-
C.
Hình vuông có hai đường chéo bằng nhau
-
D.
Hình vuông có bốn góc bằng nhau
Đáp án : B
Sử dụng dấu hiệu nhận biết của hình vuông.
Hình vuông có hai cặp cạnh đối song song => Đáp án B sai.
Khi phân tích các số \(2150;1490;2340\) ra thừa số nguyên tố thì số nào có chứa tất cả các thừa số nguyên tố \(2;3\) và \(5?\)
-
A.
$2340$
-
B.
$2150$
-
C.
$1490$
-
D.
Cả ba số trên.
Đáp án : A
Sử dụng cách phân tích một số ra thừa số nguyên tố theo hàng dọc. Từ đó xét xem số nào được phân tích ra thừa số nguyên tố mà chứa cả các thừa số nguyên tố \(2;3\) và \(5.\)
+) Phân tích số \(2150\) thành thừa số nguyên tố
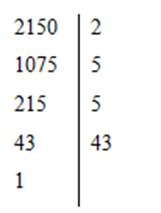
Suy ra \(2150 = {2.5^2}.43\)
+) Phân tích số \(1490\) thành thừa số nguyên tố

Suy ra \(1490 = 2.5.149\)
+) Phân tích số \(2340\) thành thừa số nguyên tố

Suy ra \(2340 = {2^2}{.3^2}.5.13\)
Vậy có số \(2340\) thỏa mãn yêu cầu đề bài.
Cho tổng A = 12 + 14 + 16 + x; x là số tự nhiên. Để A không chia hết cho 2 thì
-
A.
\(x = 199\)
-
B.
\(x = 198\)
-
C.
\(x = 1000\)
-
D.
\(x = 50054\)
Đáp án : A
Nếu tất cả các số hạng chia hết cho 2 thì A chia hết cho 2, nếu trong tổng có 1 số hạng không chia hết cho 2 thì A không chia hết cho 2.
Do 12\( \vdots \)2; 14\( \vdots \)2; 16\( \vdots \)2 nên để A \(\not\vdots \)2 thì x \(\not\vdots \)2
=> x\( \in \){1; 3; 5; 7;…} là các số lẻ.
 Điền số hoặc chữ thích hợp vào ô trống:
Điền số hoặc chữ thích hợp vào ô trống:
\(a + b + 91 = (a + b) +\)
\(=\)
\(+ (b + 91)\)
\(a + b + 91 = (a + b) +\)
\(=\)
\(+ (b + 91)\)
Áp dụng công thức: $a + b + c{\rm{ }} = {\rm{ }}\left( {a + b} \right) + c{\rm{ }} = {\rm{ }}a + \left( {b + c} \right)$
Ta có: \(a + b + 91 =\left( {a + b} \right) +91 =a + \left( {b + 91} \right)\)
Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(91\,;\,\,a\).
Cho hình vuông ABCD có chu vi bằng 28cm. Diện tích hình vuông ABCD là:
-
A.
\(49\,cm\)
-
B.
\(28\,c{m^2}\)
-
C.
\(49\,c{m^2}\)
-
D.
\(112\,c{m^2}\)
Đáp án : C
- Cạnh của hình vuông = Chu vi : 4
=> Diện tích hình vuông.
- Ta có cạnh AB = BC = CD = DA = 28 : 4 = 7 cm. - Diện tích hình vuông ABCD = 7 .7 = 49 cm 2 .
Tìm BCNN(4, 7).
-
A.
24
-
B.
21
-
C.
28
-
D.
0
Đáp án : C
Tìm B(4), B(7)
Tìm BC(4,7)
Tìm BCNN của 4 và 7: Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.
B(4) = {0; 4; 8; 12; 16; 20; 24; 28; 32; ...}
B(7) = {0; 7; 14; 21; 28; 35;... }
=> BCNN(4, 7) = 28

Trong các hình sau, hình nào là hình thoi?
A.

B.

C.

D.

B.

Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Quan sát các hình đã cho ta thấy hình A là hình thang, hình B là hình thoi, hình C là hình tròn, hình D là hình bình hành.
Vậy trong các hình đã cho, hình B là hình thoi.
Chọn câu đúng:
-
A.
Chu vi của một hình bình hành bằng tổng một cặp cạnh kề nhau bất kỳ.
-
B.
Chu vi hình bình hành bằng tổng của cạnh đáy và chiều cao.
-
C.
Chu vi hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
-
D.
Chu vi của một hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.
Đáp án : D
Sử dụng công thức tính chu vi hình bình hành.
Chu vi của một hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.
Số $x$ là bội chung của ${\rm{a;b;c}}$ nếu:
-
A.
$x \, \vdots \, a$ hoặc $x \, \vdots \, b$ hoặc $x \, \vdots \, c$
-
B.
$x \, \vdots \, a$ và $x \, \vdots \, b$
-
C.
$x \, \vdots \, b$ và $x \, \vdots \, c$
-
D.
$x \, \vdots \, a$ và $x \, \vdots \, b$ và $x \, \vdots \, c$
Đáp án : D
- Sử dụng kiến thức bội chung $2$ hay nhiều số: bội chung của $2$ hay nhiều số là bội của tất cả các số đó.
Số \(x\) là bội chung của $3$ số $a,b,c$ nếu \(x\) chia hết cho cả \(a,b,c\).
Diện tích hình thoi có độ dài hai đường chéo là 15cm và 6cm là:
-
A.
90 cm 2
-
B.
45 dm 2
-
C.
45 cm 2
-
D.
50 cm 2
Đáp án : C
Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\)
Diện tích hình thoi là: \(S = \frac{{15.6}}{2} = 45\,\,\left( {c{m^2}} \right)\).
Viết tập hợp A các số tự nhiên lớn hơn \(5\) và nhỏ hơn \(10.\)
-
A.
\(A = \left\{ {6;7;8;9} \right\}.\)
-
B.
\(A = \left\{ {5;6;7;8;9} \right\}.\)
-
C.
\(A = \left\{ {6;7;8;9;10} \right\}.\)
-
D.
\(A = \left\{ {6;7;8} \right\}.\)
Đáp án : A
Viết tập hợp \(A\) dưới dạng liệt kê các phần tử thỏa mãn đề bài.
Tập hợp A các số tự nhiên lớn hơn \(5\) và nhỏ hơn \(10\) là \(A = \left\{ {6;7;8;9} \right\}.\)
Cho phép tính \(231 - 87\). Chọn câu đúng.
-
A.
\(231\) là số trừ
-
B.
\(87\) là số bị trừ
-
C.
\(231\) là số bị trừ
-
D.
\(87\) là hiệu
Đáp án : C
Trong phép trừ $a - b = x$ thì \(a\) là số bị trừ; \(b\) là số trừ và \(x\) là hiệu.
Trong phép trừ \(231 - 87\) thì \(231\) là số bị trừ và \(87\) là số trừ nên C đúng.
Với ba chữ số \(0;1;3\) có thể viết được bao nhiêu số có ba chữ số khác nhau?
-
A.
\(4\)
-
B.
\(3\)
-
C.
\(5\)
-
D.
\(6\)
Đáp án : A
- Ta viết các số tự nhiên có ba chữ số khác nhau lập thành từ ba số \(0;1;3\) sao cho chữ số hằng trăm khác \(0\).
- Đếm các số.
Có bốn số tự nhiên thỏa mãn đề bài là \(310;301;103;130.\)
Thứ tự thực hiện phép tính nào sau đây là đúng đối với biểu thức có dấu ngoặc?
-
A.
\(\left[ {} \right] \to \left( {} \right) \to \left\{ {} \right\}\)
-
B.
\(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
-
C.
\(\left\{ {} \right\} \to \left[ {} \right] \to \left( {} \right)\)
-
D.
\(\left[ {} \right] \to \left\{ {} \right\} \to \left( {} \right)\)
Đáp án : B
Nếu biểu thức có các dấu ngoặc : ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính theo thứ tự : \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
Khẳng định nào sau đây sai ?
-
A.
\(a + b + c = \left( {a + b} \right) + c\)
-
B.
\(a + b + c = \left( {a + c} \right) + b\)
-
C.
\(a + b + c = \left( {a + b} \right) + b\)
-
D.
\(a + b + c = a + \left( {b + c} \right)\)
Đáp án : C
- Áp dụng tính chất giao hoán của phép cộng.
- Áp dụng tính chất kết hợp của phép cộng.
\(a + b + c = \left( {a + b} \right) + b\) sai vì \(c\) không thể bằng \(b\).
Trong những khẳng định sau, khẳng định nào sai ?
-
A.
Hình bình hành có 4 đỉnh
-
B.
Hình bình hành có bốn cạnh
-
C.
Hình có bốn đỉnh là hình bình hành
-
D.
Hình bình hành có hai cạnh đối song song.
Đáp án : C
Dựa vào cách nhận biết hình bình hành.
Hình bình hành có 4 đỉnh, có bốn cạnh, hai cạnh đối song song => A, B, D đúng
Hình có bốn đỉnh chưa chắc là hình bình hành, ví dụ:
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
Đáp án : A
Sử dụng dấu hiệu nhận biết hình chữ nhật
Hình chữ nhật có bốn đỉnh, hai cặp cạnh đối song song, hai đường chéo bằng nhau.
=> Đáp án B, C, D đúng.
Hình có 4 đỉnh chưa chắc là hình chữ nhật ví dụ:
Phép toán \({6^2}:4.3 + {2.5^2}\) có kết quả là:
-
A.
$77$
-
B.
$78$
-
C.
$79$
-
D.
$80$
Đáp án : A
Thực hiện phép tính nâng lên lũy thừa rồi đến nhân chia cuối cùng là cộng trừ.
Ta có \({6^2}:4.3 + {2.5^2} = 36:4.3 + 2.25 = 9.3 + 50 = 27 + 50 = 77\) .
Tìm số tự nhiên $x$ thỏa mãn: $7+x=362$.
-
A.
300
-
B.
355
-
C.
305
-
D.
362
Đáp án : B
Tìm số hạng chưa biết: Lấy tổng trừ đi số hạng đã biết.
Ta có:
$7+x=362$
$x=362-7$
$x=355$.
-
A.
\(BC\, = 5\,cm\)
-
B.
\(AC = 5\,cm\)
-
C.
\(AD = \,5\,cm\)
-
D.
\(DC = 5\,cm\)
Đáp án : D
Trong hình chữ nhật hai cạnh đối bằng nhau.
Trong hình chữ nhật ABCD, cạnh đối của cạnh AB là DC nên \(AB = DC = 5\,cm\)
Cho \(\overline {1a52} \) chia hết cho 9. Số thay thế cho \(a\) có thể là
-
A.
1
-
B.
2
-
C.
3
-
D.
5
Đáp án : A
Tìm điều kiện của \(a\).
Tính tổng các chữ số trong \(\overline {1a52} \)
Tìm \(a\) để tổng đó chia hết cho 9.
Tổng các chữ số của \(\overline {1a52} \) là \(1 + a + 5 + 2 = a + 8\) để số \(\overline {1a52} \) chia hết cho 9 thì \(a + 8\) phải chia hết cho 9.
Do a là các số tự nhiên từ 0 đến 9 nên
\(\begin{array}{l}0 + 8 \le a + 8 \le 9 + 8\\ \Rightarrow 8 \le a + 8 \le 17\end{array}\)
Số chia hết cho 9 từ 8 đến 17 chỉ có đúng một số 9, do đó \(a + 8 = 9 \Rightarrow a = 1\)
Vậy số thay thế cho a chỉ có thể là 1
Các số có chữ số tận cùng là … thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
-
A.
0, 1, 2, 3
-
B.
0, 2, 4, 6, 8
-
C.
1, 3, 5, 7, 9
-
D.
0 hoặc 5
Đáp án : D
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Kết quả của phép tính $12.100 + 100.36 - 100.19$ là
-
A.
\(29000\)
-
B.
\(3800\)
-
C.
\(290\)
-
D.
\(2900\)
Đáp án : D
Sử dụng tính chất phân phối của phép nhân với phép cộng; phép trừ \(ab + ac - ad = a\left( {b + d - c} \right).\)
Ta có $12.100 + 100.36 - 100.19$\( = 100.\left( {12 + 36 - 19} \right) = 100.29 = 2900.\)
Cho hình vẽ như sau:

Cạnh AB song song với cạnh nào dưới đây?
A. BC
B. DC
C. AD
B. DC
Quan sát hình vẽ để tìm cặp cạnh song song với nhau.
Quan sát hình vẽ ta thấy cạnh AB song song với cạnh DC.
-
A.
6 đỉnh là M, N, P, Q, R, H
-
B.
6 cạnh là MN, NP, PQ, MQ, QR, HM
-
C.
3 đường chéo chính là MQ, HP, RN.
-
D.
3 đường chéo chính cắt nhau tại 1 điểm.
Đáp án : B
- Trong hình lục giác đều:
+ 6 cạnh bằng nhau
+ 3 đường chéo chính bằng nhau.
Đáp án B sai do MQ là đường chéo chính, sửa lại:
6 cạnh là MN, NP, PQ, HR, QR, HM
Không tính giá trị cụ thể, hãy so sánh \(A = 1987657.1987655\) và \(B = 1987656.1987656\)
-
A.
\(A > B\)
-
B.
\(A < B\)
-
C.
\(A \le B\)
-
D.
\(A = B\)
Đáp án : B
Áp dụng tính chất phân phối giữa phép nhân với phép cộng để biến đổi và so sánh \(A,B.\)
Ta có \(A = 1987657.1987655\)\( = \left( {1987656 + 1} \right).1987655\)\( = 1987656.1987655 + 1987655\,\,\,\left( 1 \right)\)
Và \(B = 1987656.\left( {1987655 + 1} \right)\) \( = 1987656.1987655 + 1987656\,\,\,\left( 2 \right)\)
Vì \(1987655 < 1987656\) và từ (1) và (2) suy ra \(A < B.\)
Tìm số tự nhiên \(x\) biết rằng \(x - 50:25 = 8.\)
-
A.
\(11\)
-
B.
\(250\)
-
C.
\(10\)
-
D.
\(20\)
Đáp án : C
Thực hiện phép chia trước rồi tìm \(x\) bằng cách lấy hiệu cộng với số trừ.
Ta có \(x - 50:25 = 8\)
\(x - 2 = 8\)
\(x = 8 + 2\)
\(x = 10.\)
Tính giá trị của biểu thức \(A = \dfrac{{{{11.3}^{22}}{{.3}^7} - {9^{15}}}}{{{{\left( {{{2.3}^{13}}} \right)}^2}}}\)
-
A.
\(A = 18\)
-
B.
\(A = 9\)
-
C.
\(A = 54.\)
-
D.
\(A = 6\)
Đáp án : C
Sử dụng các công thức ${a^m}.{a^n} = {a^{m + n}};{a^m}:{a^n} = {a^{m - n}};\,$${\left( {{a^m}} \right)^n} = {a^{m.n}};\,{\left( {ab} \right)^m} = {a^m}.{b^m}\left( {a;b \ne 0,m \ge n} \right).$
Và tính chất \(ab - ac = a\left( {b - c} \right).\)
Ta có \(A = \dfrac{{{{11.3}^{22}}{{.3}^7} - {9^{15}}}}{{{{\left( {{{2.3}^{13}}} \right)}^2}}}\)\( = \dfrac{{{{11.3}^{22 + 7}} - {{\left( {{3^2}} \right)}^{15}}}}{{{2^2}.{{\left( {{3^{13}}} \right)}^2}}}\)\( = \dfrac{{{{11.3}^{29}} - {3^{2.15}}}}{{{2^2}{{.3}^{13.2}}}}\)\( = \dfrac{{{{11.3}^{29}} - {3^{30}}}}{{{2^2}{{.3}^{26}}}}\)\( = \dfrac{{{{11.3}^{29}} - {3^{29}}.3}}{{{2^2}{{.3}^{26}}}}\)
\( = \dfrac{{{3^{29}}\left( {11 - 3} \right)}}{{{2^2}{{.3}^{26}}}} = \dfrac{{{3^{29}}.8}}{{{{4.3}^{26}}}} = {2.3^{29 - 26}} = {2.3^3} = 54.\)
Vậy \(A = 54.\)
Có bao nhiêu số tự nhiên \(n\) để \( (n + 4) \, \vdots \, n\) ?
-
A.
\(3\)
-
B.
\(4\)
-
C.
\(2\)
-
D.
\(1\)
Đáp án : A
Sử dụng tính chất 1: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó để suy ra điều kiện của \(n.\)
Vì \(n \, \vdots \, n\) nên để \((n + 4) \, \vdots \, n\) thì \(4 \, \vdots \, n\) suy ra \(n \in \left\{ {1;2;4} \right\}\)
Vậy có ba giá trị của \(n\) thỏa mãn điều kiện đề bài.

Từ ba chữ số $2\,;\,\,5\,;\,\,8{\rm{ }}$ hãy viết các số có hai chữ số khác nhau và chia hết cho \(5\).
A. \(28\,;\,\,58\)
B.\(\,25;\,\,85\)
C. \(25\,\, ;\,\,\,58\,\)
D. \(25\,;\,55\,;\,85\,\)
B.\(\,25;\,\,85\)
Viết các số có hai chữ số khác nhau từ ba chữ số $2;\,5;\,8{\rm{ }}$.
Số nào có chữ số tận cùng là \(0\) hoặc \(5\) thì không chia hết cho \(5\).
Từ ba chữ số $2;\,\,5;\,\,8$ viết được các số có hai chữ số khác nhau là \(25\,;\,\,28\,;\,\,52\,;\,\,58\,;\,\,82\,;\,\,85\).
Các số \(\,25;\,\,85\) có chữ số tận cùng là \(5\) nên chia hết cho \(5\).
Vậy từ ba chữ số $2;\,\,5;\,\,8{\rm{ }}$ ta viết được các số có hai chữ số khác nhau và chia hết cho \(5\) là \(\,25;\,\,85\).
Tìm các chữ số $x, y$ biết rằng: \(\overline {23x5y} \) chia hết cho $2; 5$ và $9.$
-
A.
\(x = 0;y = 6\)
-
B.
\(x = 6;y = 0\)
-
C.
\(x = 8;y = 0\)
-
D.
\(x = 0;y = 8\)
Đáp án : C
Điều kiện: \(x; y \in \left\{ {0;\,\,1;\,\,2;\,\,.......;\,\,9} \right\}\)
Vì \(\overline {23x5y} \) chia hết cho cả $2$ và $5$ nên \(y = 0\) ta được số \(\overline {23x50} \) .
Số \(\overline {23x50} \,\, \vdots \,\,9 \Rightarrow \left( {2 + 3 + x + 5 + 0} \right)\,\, \vdots \,\,9 \Rightarrow \left( {10 + x} \right)\,\, \vdots \,\,9 \Rightarrow x = 8.\)
Vậy \(x = 8;y = 0\), ta có số $23850.$
Một hình vuông có diện tích là \(1936\,{m^2}.\) Tính cạnh của hình vuông đó.
-
A.
$44$
-
B.
$46$
-
C.
$22$
-
D.
$48$
Đáp án : A
+ Phân tích số \(1936\) ra thừa số nguyên tố, từ đó phân tích thành tích các thừa số.
+ Dựa vào bốn cạnh hình vuông bằng nhau và diện tích hình vuông bằng cạnh nhân cạnh để tìm các thừa số phù hợp. Đó chính là độ dài cạnh hình vuông.
Phân tích số \(1936\) ra thừa số nguyên tố ta được

Hay \(1936 = {2^4}{.11^2} = \left( {{2^2}.11} \right).\left( {{2^2}.11} \right) = 44.44\)
Vậy cạnh hình vuông bằng \(44\,m.\)
Tìm \(x\) biết $120$ $ \vdots $ $x$; $200$ $ \vdots $ $x$ và \(x < 40\)
-
A.
\(x \in \left\{ {1;2;4;5;8;10;20} \right\}\)
-
B.
\(x \in \left\{ {2;5;10;20;40} \right\}\)
-
C.
\(x \in \left\{ {1;2;5;10;20;40} \right\}\)
-
D.
\(x \in \left\{ {2;5;10;20} \right\}\)
Đáp án : A
+Tìm các ước chung nhỏ hơn \(40\) của \(120\) và \(200.\)
+) Vì \(120 \, \vdots \, x\) nên \(x \in \)Ư\(\left( {120} \right)\)\( = \left\{ {1;2;3;4;5;6;8;10;12;15;20;24;30;40;60;120} \right\}\)
+) Vì \(200 \, \vdots \, x\) nên \(x \in \)Ư\(\left( {200} \right)\)\( = \left\{ {1;2;4;5;8;10;20;25; 40;50;100;200} \right\}\)
Nên \(x \in \)ƯC\(\left( {120;200} \right) = \left\{ {1;2;4;5;8;10;20;40} \right\}\) mà \(x < 40\) nên \(x \in \left\{ {1;2;4; 5;8;10;20} \right\}.\)
Tính diện tích của hình thoi có tổng độ dài hai đường chéo là 30cm và đường chéo lớn hơn đường chéo bé 2cm.
-
A.
110 cm 2
-
B.
112 cm 2
-
C.
111 cm 2
-
D.
114 cm 2
Đáp án : B
- Độ dài đường chéo lớn = (Tổng độ dài hai đường chéo + Hiệu độ dài hai đường chéo) : 2
=> Độ dài đường chéo bé = Tổng độ dài hai đường chéo - Độ dài đường chéo lớn
- Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\).
Độ dài đường chéo lớn là: \(\left( {30 + 2} \right):2 = 16\,\left( {cm} \right)\)
Độ dài đường chéo bé là: \(30 - 16 = 14\left( {cm} \right)\)
Diện tích hình thoi là: \(\frac{{16.14}}{2} = 112\left( {c{m^2}} \right)\)
Để đánh số các trang của một quyển sách người ta phải dùng tất cả \(600\) chữ số. Hỏi quyển sách có bao nhiêu trang?
-
A.
\(326\)
-
B.
\(136\)
-
C.
\(263\)
-
D.
\(236\)
Đáp án : D
Chia ra thành các trang đánh \(1\) chữ số; \(2\) chữ số và \(3\) chữ số để tìm số trang của quyển sách.
\(99\) trang đầu cần dùng \(9.1 + 90.2 = 189\) chữ số
\(999\) trang đầu cần dùng \(9.1 + 90.2 + 900.3 = 2889\) chữ số
Vì \(189 < 600 < 2889\) nên trang cuối cùng phải có ba chữ số
Số chữ số dùng để đánh số trang có ba chữ số là \(600 - 189 = 411\) (chữ số)
Số trang có ba chữ số là \(411:3 = 137\) trang
Số trang của quyển sách là \(99 + 137 = 236\) trang
 Tìm \(x\) biết: \(45 + (1234 + x) = 1234 + (45 + 120)\)
Tìm \(x\) biết: \(45 + (1234 + x) = 1234 + (45 + 120)\)
A. \(x = 120\)
B. \(x = 125\)
C. \(x = 145\)
D. \(x = 165\)
A. \(x = 120\)
Áp dụng tính chất giao hoán và kết hợp của phép cộng.
Ta có: $45 + \left( {1234 + x} \right){\rm{ }} = {\rm{ }}45 + 1234 + x = 1234 + \left( {45+x} \right)$
Theo đề bài ta có: \(45 + (1234 + x) = 1234 + (45 + 120)\)
Nên: $1234 + \left( {45+x} \right) = 1234 + \left( {45{\rm{ + 120}}} \right)$
Từ đó suy ra \(x = 120\).

Điền số thích hợp vào ô trống:
Từ bốn chữ số $0;{\rm{ 3; 5;}}\,\,9$ có thể viết được
số có ba chữ số khác nhau và chia hết cho \(5\).
Từ bốn chữ số $0;{\rm{ 3; 5;}}\,\,9$ có thể viết được
số có ba chữ số khác nhau và chia hết cho \(5\).
Áp dụng tính chất các số chữ số tận cùng là \(0\) hoặc \(5\) thì chia hết cho \(5\) để viết các số có ba chữ số khác nhau từ bốn chữ số trên mà chia hết cho \(5\).
Ta đếm số lượng các số chia hết cho \(5\) và điền vào ô trống.
Để lập được số chia hết cho \(5\) thì các số đó phải có chữ số tận cùng là \(0\) hoặc \(5\).
Từ bốn chữ số $0;{\rm{ 3; 5;}}\,9$ ta viết được các số có ba chữ số khác nhau và chia hết cho \(5\) là:
\(350\,;\,\,390\,;\,530\,;\,\,590;\,\,930\,;\,\,950;\,\,\,305\,;\,\,395\,;\,\,905\,;935\).
Có \(10\) số có ba chữ số khác nhau và chia hết cho \(5\). Vậy đáp án đúng điền vào ô trống là \(10\).
Sân trường em hình vuông. Để tăng thêm diện tích nhà trường mở rộng về mỗi phía 4m thì diện tích tăng thêm 192m 2 . Hỏi trước đây sân trường em có diện tích là bao nhiêu m 2 ?
-
A.
16 m 2
-
B.
32 m 2
-
C.
64 m 2
-
D.
128 m 2
Đáp án : C
- Diện tích tăng thêm bằng diện tích 4 hình vuông nhỏ cạnh bằng 4m và 4 hình chữ nhật có 1 cạnh bằng 4 m và 1 cạnh bằng cạnh hình vuông
- Tinh diện tích 4 hình vuông nhỏ
- Tính diện tích 4 hình chữ nhật
- Tính diện tích 1 hình chữ nhật
- Tính cạnh hình vuông đã cho
=> Diện tích sân trường lúc chưa mở rộng.
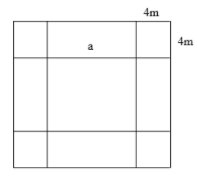
Diện tích tăng thêm bằng diện tích 4 hình vuông nhỏ cạnh bằng 4m và 4 hình chữ nhật có 1 cạnh bằng 4 m và 1 cạnh bằng cạnh hình vuông
Diện tích 4 hình vuông nhỏ là: 4 . (4 . 4) = 64 m 2
Diện tích 4 hình chữ nhật là: 192 - 64 = 128 m 2
Diện tích 1 hình chữ nhật là 128 : 4 = 32 m 2
Cạnh hình vuông đã cho là: 32 : 4 = 8 m
Diện tích sân trường lúc chưa mở rộng là: 8 . 8 = 64 m 2