Đề kiểm tra giữa học kì 1 Toán 6 Kết nối tri thức - Đề số 2
Đề bài
Dạng tổng quát của số tự nhiên chia cho \(5\) dư \(2\) là
-
A.
\(2k + 5\,\left( {k \in N} \right)\)
-
B.
\(5k + 2\,\left( {k \in N} \right)\)
-
C.
\(2k\,\left( {k \in N} \right)\)
-
D.
\(5k + 4\,\left( {k \in N} \right)\)
Chọn câu đúng:
-
A.
Diện tích hình bình hành bằng nửa tích của cạnh đáy nhân với chiều cao.
-
B.
Diện tích hình bình hành bằng tổng của cạnh đáy và chiều cao.
-
C.
Diện tích hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
-
D.
Diện tích hình bình hành bằng hiệu của cạnh đáy và chiều cao.
Kết quả của phép tính $12.100 + 100.36 - 100.19$ là
-
A.
\(29000\)
-
B.
\(3800\)
-
C.
\(290\)
-
D.
\(2900\)
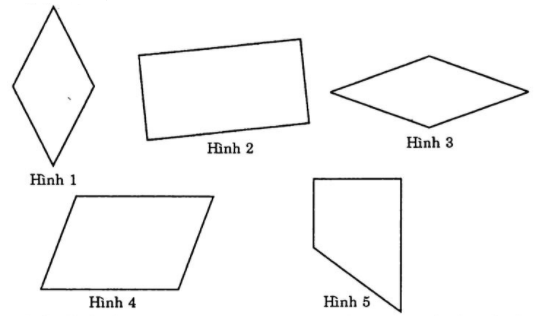
-
A.
Hình 1, Hình 2
-
B.
Hình 3, Hình 4
-
C.
Hình 1, Hình 3
-
D.
Hình 3, Hình 5
Thực hiện các phép tính sau:\(\dfrac{3}{8} + \dfrac{5}{{24}}\). Với kết quả là phân số tối giản.
-
A.
\(\dfrac{{14}}{{24}}\)
-
B.
\(\dfrac{7}{{12}}\)
-
C.
\(\dfrac{{112}}{{192}}\)
-
D.
\(\dfrac{{12}}{7}\)
Một ước nguyên tố của 91 là
-
A.
1
-
B.
2
-
C.
3
-
D.
7
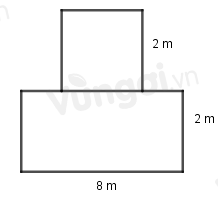
-
A.
4 m 2
-
B.
16 m 2
-
C.
20 m 2
-
D.
24 m 2
Viết tập hợp A các số tự nhiên lớn hơn \(5\) và nhỏ hơn \(10.\)
-
A.
\(A = \left\{ {6;7;8;9} \right\}.\)
-
B.
\(A = \left\{ {5;6;7;8;9} \right\}.\)
-
C.
\(A = \left\{ {6;7;8;9;10} \right\}.\)
-
D.
\(A = \left\{ {6;7;8} \right\}.\)

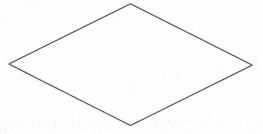
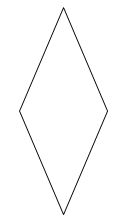
Trong các hình sau, hình nào là hình thoi?

Cho tổng: \(15946 + ? = 51612 + 15946\). Dấu “?” trong tổng trên là:
-
A.
\(51612\)
-
B.
\(15946\)
-
C.
\(67558\)
-
D.
\(35666\)
Nếu \(x \, \vdots \, 2\) và \(y \, \vdots \, 4\) thì tổng \(x + y\) chia hết cho
-
A.
$2$
-
B.
$4$
-
C.
$8$
-
D.
không xác định
Số $x$ là ước chung của số $a$ và số $b$ nếu:
-
A.
$x \in $Ư$\left( a \right)$ và $x \in B(b)$
-
B.
$x \subset Ư(a)$và $x \subset Ư(b)$
-
C.
$x \in $Ư\(\left( a \right)\) và $x \in $Ư\(\left( b \right)\)
-
D.
$x \notin Ư(a)$ và $x \notin Ư(b)$
Tìm ước chung của $9$ và $15$.
-
A.
${\rm{\{ 1;3\} }}$
-
B.
${\rm{\{ 0;3\} }}$
-
C.
${\rm{\{ 1;5\} }}$
-
D.
${\rm{\{ 1;3;9\} }}$
Viết các tập hợp $Ư(6);Ư(20);ƯC(6,20).$
-
A.
Ư$(6) = \left\{ {{\rm{1,2,3,6}}} \right\}$; Ư${\rm{(20) = }}\left\{ {{\rm{1,2,4,5,10,20}}} \right\}$; ƯC${\rm{(6,20) = }}\left\{ {{\rm{1,2}}} \right\}$
-
B.
Ư$(6) = \left\{ {{\rm{1,2,3,6}}} \right\}$; Ư${\rm{(20) = }}\left\{ {{\rm{1,2,4,5,20}}} \right\}$; ƯC${\rm{(6,20) = }}\left\{ {{\rm{1,2}}} \right\}$
-
C.
Ư$(6) = \left\{ {{\rm{1,2,3}}} \right\}$; Ư${\rm{(20) = }}\left\{ {{\rm{1,2,4,5,10,20}}} \right\}$; ƯC${\rm{(6,20) = }}\left\{ {{\rm{1,2}}} \right\}$
-
D.
Ư$(6) = \left\{ {{\rm{1,2,4,6}}} \right\}$; Ư${\rm{(20) = }}\left\{ {{\rm{1,2,4,20}}} \right\}$; ƯC${\rm{(6,20) = }}\left\{ {{\rm{1,2,4}}} \right\}$
Phát biểu nào sau đây sai ?
-
A.
Hình lục giác đều có 6 đỉnh
-
B.
Hình lục giác đều có 6 cạnh
-
C.
Hình lục giác đều có 6 đường chéo chính
-
D.
Hình lục giác đều có 6 góc
-
A.
A={Hình chữ nhật, hình vuông, hình tam giác}
-
B.
A={Hình chữ nhật, hình vuông, hình tam giác, hình bình hành}
-
C.
A={Hình chữ nhật, hình vuông, hình tam giác, hình bình hành, hình thang cân}
-
D.
A={Hình chữ nhật, hình vuông, hình tam giác, hình bình hành, hình thang}
Cho hình vẽ như sau:
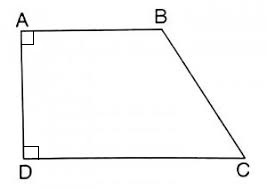
Cạnh AB song song với cạnh nào dưới đây?
A. BC
B. DC
C. AD
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là 0
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung
Các số có … chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
-
A.
các chữ số
-
B.
tổng các chữ số
-
C.
tổng
-
D.
chữ số tận cùng
Trong các số $333; 354; 360; 2457; 1617; 152,$ các số chia hết cho $9$ là
-
A.
$333$
-
B.
$360$
-
C.
$2457$
-
D.
Cả A, B, C đều đúng
Cho \(a \vdots m\) và \(b \vdots m\) và \(c \vdots m\) với m là số tự nhiên khác 0. Các số a,b,c là số tự nhiên tùy ý.
Khẳng định nào sau đây chưa đúng?
(Xét trong tập số tự nhiên, số bị trừ phải lớn hơn hoặc bằng số trừ)
-
A.
\(\left( {a + b} \right) \vdots m\)
-
B.
\(\left( {a - b} \right) \vdots m\)
-
C.
\(\left( {a + b + c} \right) \vdots m\)
-
D.
\(\left( {b + c} \right) \vdots m\)
Tính nhanh tổng \(53 + 25 + 47 + 75\)?
-
A.
\(200\)
-
B.
\(201\)
-
C.
\(100\)
-
D.
\(300\)
Chu vi và diện tích hình vuông có cạnh là 7 cm lần lượt là
-
A.
\(28\,\,cm;\,\,49\,cm\)
-
B.
\(28\,\,c{m^2};\,\,49\,cm\)
-
C.
\(49\,cm;\,\,28\,\,c{m^2}\)
-
D.
\(28\,\,cm;\,\,49\,c{m^2}\)
Tính: \(1 + 12.3.5\)
-
A.
181
-
B.
195
-
C.
180
-
D.
15
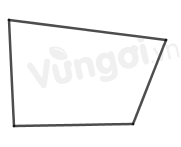
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
Các số có chữ số tận cùng là … thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
-
A.
0, 1, 2, 3
-
B.
0, 2, 4, 6, 8
-
C.
1, 3, 5, 7, 9
-
D.
0 hoặc 5
Trong các số 3,5,8,9, số nào thuộc tập hợp \(A = \left\{ {x \in \mathbb{N}\left| {x \ge 8} \right.} \right\}\) , số nào thuộc tập hợp \(B = \left\{ {x \in \mathbb{N}\left| {x < 5} \right.} \right\}\) ?
-
A.
9 thuộc A; 3 và 5 thuộc B
-
B.
9 thuộc A; 3, 5, 8 thuộc B
-
C.
8 và 9 thuộc A; 3 và 5 thuộc B
-
D.
8 và 9 thuộc A; 3 thuộc B.
Tìm số tự nhiên \(n\) biết \({3^n} = 81.\)
-
A.
\(n = 2\)
-
B.
\(n = 4\)
-
C.
\(n = 5\)
-
D.
\(n = 8\)
Giá trị của biểu thức \(2\left[ {\left( {195 + 35:7} \right):8 + 195} \right] - 400\) bằng
-
A.
$140$
-
B.
$60$
-
C.
$80$
-
D.
$40$
Tìm số tự nhiên \(x\) biết rằng \(x - 50:25 = 8.\)
-
A.
\(11\)
-
B.
\(250\)
-
C.
\(10\)
-
D.
\(20\)
Số tự nhiên \(x\) nào dưới đây thỏa mãn \({4^x} = {4^3}{.4^5}?\)
-
A.
\(x = 32\)
-
B.
\(x = 16\)
-
C.
\(x = 4\)
-
D.
\(x = 8\)
Có bao nhiêu giá trị của \(x\) thỏa mãn \(240 - \left[ {23 + \left( {13 + 24.3 - x} \right)} \right] = 132?\)
-
A.
$3$
-
B.
$2$
-
C.
$1$
-
D.
$4$
Dùng ba trong bốn chữ số \(5;8;4;0\) hãy lập ra các số tự nhiên chia hết cho \(3\) mà không chia hết cho \(9.\)
-
A.
\(840;804;408\)
-
B.
\(840;804;408;480\)
-
C.
\(540;450;405\)
-
D.
\(540;450;405;504\)
Có bao nhiêu số tự nhiên \(x\) khác \(0\) thỏa mãn $x \in BC(12 ; 15 ; 20) $ và $x$ $ \le $ $100$
-
A.
$4$
-
B.
$3$
-
C.
$2$
-
D.
$1$

Độ dài đáy của hình bình hành có chiều cao \(24cm\) và diện tích là \(432c{m^2}\) là:
A. \(16cm\)
B. \(17cm\)
C. \(18cm\)
D. \(19cm\)
Một mảnh giấy hình chữ nhật có diện tích \(96 cm^2\). Một cạnh có độ dài 12 cm. Tính chu vi của mảnh giấy đó?
-
A.
8 cm
-
B.
20 cm
-
C.
40 cm
-
D.
80 cm

Điền số thích hợp vào ô trống:
Từ bốn chữ số $0;{\rm{ 3; 5;}}\,\,9$ có thể viết được
số có ba chữ số khác nhau và chia hết cho \(5\).
-
A.
91 m 2
-
B.
18 m 2
-
C.
87 m 2
-
D.
69 m 2
Một miếng đất hình chữ nhật có chiều dài 64 m, chiều rộng 34 m. Người ta giảm chiều dài và tăng chiều rộng để miếng đất là hình vuông, biết phần diện tích giảm theo chiều dài là 272. Tìm phần diện tích tăng thêm theo chiều rộng.
-
A.
\(176\,{m^2}\)
-
B.
\(2176\,{m^2}\)
-
C.
\(1232\,{m^2}\)
-
D.
\(3136\,{m^2}\)
-
A.
9
-
B.
14
-
C.
10
-
D.
13
Lời giải và đáp án
Dạng tổng quát của số tự nhiên chia cho \(5\) dư \(2\) là
-
A.
\(2k + 5\,\left( {k \in N} \right)\)
-
B.
\(5k + 2\,\left( {k \in N} \right)\)
-
C.
\(2k\,\left( {k \in N} \right)\)
-
D.
\(5k + 4\,\left( {k \in N} \right)\)
Đáp án : B
Số tự nhiên \(a\) chia cho \(b\) được thương \(q\) và dư $r$ có dạng \(a = b.q + r.\)
Dạng tổng quát của số tự nhiên chia cho \(5\) dư \(2\) là \(a = 5k + 2\,\left( {k \in N} \right).\)
Chọn câu đúng:
-
A.
Diện tích hình bình hành bằng nửa tích của cạnh đáy nhân với chiều cao.
-
B.
Diện tích hình bình hành bằng tổng của cạnh đáy và chiều cao.
-
C.
Diện tích hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
-
D.
Diện tích hình bình hành bằng hiệu của cạnh đáy và chiều cao.
Đáp án : C
Diện tích hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
Kết quả của phép tính $12.100 + 100.36 - 100.19$ là
-
A.
\(29000\)
-
B.
\(3800\)
-
C.
\(290\)
-
D.
\(2900\)
Đáp án : D
Sử dụng tính chất phân phối của phép nhân với phép cộng; phép trừ \(ab + ac - ad = a\left( {b + d - c} \right).\)
Ta có $12.100 + 100.36 - 100.19$\( = 100.\left( {12 + 36 - 19} \right) = 100.29 = 2900.\)
-
A.
Hình 1, Hình 2
-
B.
Hình 3, Hình 4
-
C.
Hình 1, Hình 3
-
D.
Hình 3, Hình 5
Đáp án : C
Hình thoi là hình tứ giác có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Hình thoi là hình tứ giác có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
=> Hình 1 và Hình 3 là hình thoi
Thực hiện các phép tính sau:\(\dfrac{3}{8} + \dfrac{5}{{24}}\). Với kết quả là phân số tối giản.
-
A.
\(\dfrac{{14}}{{24}}\)
-
B.
\(\dfrac{7}{{12}}\)
-
C.
\(\dfrac{{112}}{{192}}\)
-
D.
\(\dfrac{{12}}{7}\)
Đáp án : B
- Để quy đồng mẫu hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\), ta phải tìm mẫu chung của hai phân số đó. Thông thường ta nên chọn mẫu chung là bội chung nhỏ nhất của hai mẫu.
- Để cộng, trừ các phân số khác mẫu ta đi quy đồng mẫu số các phân số rồi thực hiện cộng(trừ) tử số và giữ nguyên mẫu.
Ta có BCNN(8; 24) = 24 nên:
\(\dfrac{3}{8} + \dfrac{5}{{24}} = \dfrac{{3.3}}{{8.3}} + \dfrac{5}{{24}} = \dfrac{9}{{24}} + \dfrac{5}{{24}} = \dfrac{{14}}{{24}} = \dfrac{7}{{12}}\)
Một ước nguyên tố của 91 là
-
A.
1
-
B.
2
-
C.
3
-
D.
7
Đáp án : D
Ước nguyên tố của số a là một ước của a và ước đó là số nguyên tố.
91 có tổng các chữ số bằng 10 không chia hết cho 3 nên 3 không là ước nguyên tố của 91
91 có chữ số tận cùng là 1 nên 91 không chia hết cho 2, do đó 2 không là ước nguyên tố.
Một ước số nguyên tố của 91 là: 7.
-
A.
4 m 2
-
B.
16 m 2
-
C.
20 m 2
-
D.
24 m 2
Đáp án : C
Diện tích mảnh vườn = Diện tích phần đất hình vuông + Diện tích phần đất hình chữ nhật.
+ Diện tích hình vuông = Cạnh . Cạnh
+ Diện tích hình chữ nhật = Chiều dài . chiều rộng
Diện tích phần đất hình vuông là: \({2^2} = 4\left( {{m^2}} \right)\)
Diện tích phần đất hình chữ nhật là: \(8.2 = 16\left( {{m^2}} \right)\)
Diện tích mảnh vườn là: \(4 + 16 = 20\,\left( {{m^2}} \right)\)
Viết tập hợp A các số tự nhiên lớn hơn \(5\) và nhỏ hơn \(10.\)
-
A.
\(A = \left\{ {6;7;8;9} \right\}.\)
-
B.
\(A = \left\{ {5;6;7;8;9} \right\}.\)
-
C.
\(A = \left\{ {6;7;8;9;10} \right\}.\)
-
D.
\(A = \left\{ {6;7;8} \right\}.\)
Đáp án : A
Viết tập hợp \(A\) dưới dạng liệt kê các phần tử thỏa mãn đề bài.
Tập hợp A các số tự nhiên lớn hơn \(5\) và nhỏ hơn \(10\) là \(A = \left\{ {6;7;8;9} \right\}.\)

Trong các hình sau, hình nào là hình thoi?






Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Quan sát các hình đã cho ta thấy hình thứ nhất và thứ hai từ trên xuống là hình thoi.
Hình thứ ba là hình thang và hình thứ tư là hình bình hành.
Cho tổng: \(15946 + ? = 51612 + 15946\). Dấu “?” trong tổng trên là:
-
A.
\(51612\)
-
B.
\(15946\)
-
C.
\(67558\)
-
D.
\(35666\)
Đáp án : A
Áp dụng tính chất giao hoán của phép cộng.
Áp dụng tính chất giao hoán của phép cộng ta có:
\(15946 + 51612 = 51612 + 15946\). Suy ra "?" có giá trị \(51612\).
Nếu \(x \, \vdots \, 2\) và \(y \, \vdots \, 4\) thì tổng \(x + y\) chia hết cho
-
A.
$2$
-
B.
$4$
-
C.
$8$
-
D.
không xác định
Đáp án : A
Tính chất 1: Nếu số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
Ta có: \(x\,\, \vdots \,\,2;\,\,y\,\, \vdots \,\,4 \Rightarrow y\,\, \vdots \,\,2 \Rightarrow \left( {x + y} \right)\,\, \vdots \,\,2\)
Số $x$ là ước chung của số $a$ và số $b$ nếu:
-
A.
$x \in $Ư$\left( a \right)$ và $x \in B(b)$
-
B.
$x \subset Ư(a)$và $x \subset Ư(b)$
-
C.
$x \in $Ư\(\left( a \right)\) và $x \in $Ư\(\left( b \right)\)
-
D.
$x \notin Ư(a)$ và $x \notin Ư(b)$
Đáp án : C
- Sử dụng kiến ước chung của $2$ số: ước chung của $2$ hay nhiều số là ước của tất cả các số đó.
Số \(x\) là ước chung của \(a,b\) nếu \(x\) vừa là ước của \(a\) vừa là ước của \(b\).
Tìm ước chung của $9$ và $15$.
-
A.
${\rm{\{ 1;3\} }}$
-
B.
${\rm{\{ 0;3\} }}$
-
C.
${\rm{\{ 1;5\} }}$
-
D.
${\rm{\{ 1;3;9\} }}$
Đáp án : A
- Tìm ước của \(9\) và \(15\).
- Tìm các ước chung của $2$ hay số.
- Ta có:
Ư$(9) = {\rm{\{ 1,3,9\} }}$ và Ư$(15) = {\rm{\{ 1,3,5,15\} }}$
Vậy ƯC$(9,15) = $Ư\(\left( 9 \right) \cap \) Ư\(\left( {15} \right)\)$ = {\rm{\{ 1,3\} }}$
Viết các tập hợp $Ư(6);Ư(20);ƯC(6,20).$
-
A.
Ư$(6) = \left\{ {{\rm{1,2,3,6}}} \right\}$; Ư${\rm{(20) = }}\left\{ {{\rm{1,2,4,5,10,20}}} \right\}$; ƯC${\rm{(6,20) = }}\left\{ {{\rm{1,2}}} \right\}$
-
B.
Ư$(6) = \left\{ {{\rm{1,2,3,6}}} \right\}$; Ư${\rm{(20) = }}\left\{ {{\rm{1,2,4,5,20}}} \right\}$; ƯC${\rm{(6,20) = }}\left\{ {{\rm{1,2}}} \right\}$
-
C.
Ư$(6) = \left\{ {{\rm{1,2,3}}} \right\}$; Ư${\rm{(20) = }}\left\{ {{\rm{1,2,4,5,10,20}}} \right\}$; ƯC${\rm{(6,20) = }}\left\{ {{\rm{1,2}}} \right\}$
-
D.
Ư$(6) = \left\{ {{\rm{1,2,4,6}}} \right\}$; Ư${\rm{(20) = }}\left\{ {{\rm{1,2,4,20}}} \right\}$; ƯC${\rm{(6,20) = }}\left\{ {{\rm{1,2,4}}} \right\}$
Đáp án : A
- Sử dụng kiến thức ước của một số và ước chung của hai hay nhiều số.
- Viết (liệt kê) các phần tử tập hợp.
Ta có:
Ư$(6) = \left\{ {{\rm{1,2,3,6}}} \right\}$ và Ư${\rm{(20) = }}\left\{ {{\rm{1,2,4,5,10,20}}} \right\}$
Vậy ƯC${\rm{(6,20) = }}\left\{ {{\rm{1,2}}} \right\}$
Phát biểu nào sau đây sai ?
-
A.
Hình lục giác đều có 6 đỉnh
-
B.
Hình lục giác đều có 6 cạnh
-
C.
Hình lục giác đều có 6 đường chéo chính
-
D.
Hình lục giác đều có 6 góc
Đáp án : C
Sử dụng dấu hiệu nhận biết lục giác đều.
Các đáp án A, B, D đúng.
Hình lục giác đều có 3 đường chéo chính => Đáp án C sai .
-
A.
A={Hình chữ nhật, hình vuông, hình tam giác}
-
B.
A={Hình chữ nhật, hình vuông, hình tam giác, hình bình hành}
-
C.
A={Hình chữ nhật, hình vuông, hình tam giác, hình bình hành, hình thang cân}
-
D.
A={Hình chữ nhật, hình vuông, hình tam giác, hình bình hành, hình thang}
Đáp án : D
+) Quan sát và nhận dạng các hình.
+) Các phần tử của A viết trong dấu ngoặc nhọn { }, cách nhau bởi dấu phẩy “,”
+) Các phần tử là tên các loại hình học.
Các hình trên theo thứ tự từ trái sang phải lần lượt là hình chữ nhật, hình vuông, hình bình hành, hình tam giác, hình thang.
Vậy A = {hình chữ nhật, hình vuông, hình bình hành, hình tam giác, hình thang}
Cho hình vẽ như sau:

Cạnh AB song song với cạnh nào dưới đây?
A. BC
B. DC
C. AD
B. DC
Quan sát hình vẽ để tìm cặp cạnh song song với nhau.
Quan sát hình vẽ ta thấy cạnh AB song song với cạnh DC.
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là 0
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung
Đáp án : A
- Áp dụng kiến thức:
Mọi số tự nhiên đều có ước là $1$.
Số nguyên tố có $2$ ước là $1$ và chính nó.
Mọi số nguyên tố khác nhau đều có ước chung duy nhất là $1$.
A. Đáp án này đúng vì mọi số tự nhiên đều có ước chung là $1$
B. Đáp án này sai, vì $0$ không là ước của $1$ số nào cả.
C. Đáp án này sai, vì số nguyên tố có $2$ ước là $1$ và chính nó.
D. Đáp án này sai, vì $2$ số nguyên tố có ước chung là $1$.
Các số có … chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
-
A.
các chữ số
-
B.
tổng các chữ số
-
C.
tổng
-
D.
chữ số tận cùng
Đáp án : B
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
Trong các số $333; 354; 360; 2457; 1617; 152,$ các số chia hết cho $9$ là
-
A.
$333$
-
B.
$360$
-
C.
$2457$
-
D.
Cả A, B, C đều đúng
Đáp án : D
Sử dụng dấu hiệu chia hết cho $9$ : Các số có tổng các chữ số chia hết cho $9$ thì chia hết cho $9.$
Các số $333;2457;360$ là các số chia hết cho $9$ vì tổng các chữ số của nó chia hết cho $9.$
+) Số $333$ có tổng các chữ số là $3+3+3=9 \, \vdots \, 9$ nên $ 333 \, \vdots \, 9.$
+) Số $2457$ có tổng các chữ số là $2+4+5+7=18 \, \vdots \, 9$ nên $ 2457 \, \vdots \, 9.$
+) Số $360$ có tổng các chữ số là $3+6+0=9 \, \vdots \, 9$ nên $ 360 \, \vdots \, 9.$
Các số còn lại $354; 1617; 152$ đều có tổng các chữ số không chia hết cho $9$ nên chúng không chia hết cho $9$.
Cho \(a \vdots m\) và \(b \vdots m\) và \(c \vdots m\) với m là số tự nhiên khác 0. Các số a,b,c là số tự nhiên tùy ý.
Khẳng định nào sau đây chưa đúng?
(Xét trong tập số tự nhiên, số bị trừ phải lớn hơn hoặc bằng số trừ)
-
A.
\(\left( {a + b} \right) \vdots m\)
-
B.
\(\left( {a - b} \right) \vdots m\)
-
C.
\(\left( {a + b + c} \right) \vdots m\)
-
D.
\(\left( {b + c} \right) \vdots m\)
Đáp án : B
Tính chất 1 : Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
\(a \vdots m\) và \(b \vdots m\) \( \Rightarrow \left( {a + b} \right) \vdots m\)
\(a \vdots m\) và \(b \vdots m\) \( \Rightarrow \left( {a - b} \right) \vdots m\) với \(\left( {a \ge b} \right)\)
\(a \vdots m;b \vdots m;c \vdots m \Rightarrow \left( {a + b + c} \right) \vdots m\)
\(\left( {a - b} \right) \vdots m\) sai vì thiếu điều kiện \(a \ge b\)
Tính nhanh tổng \(53 + 25 + 47 + 75\)?
-
A.
\(200\)
-
B.
\(201\)
-
C.
\(100\)
-
D.
\(300\)
Đáp án : A
Sử dụng tính chất giao hoán của phép cộng để tính nhanh tổng đã cho
Ta có \(53 + 25 + 47 + 75\)\( = \left( {53 + 47} \right) + \left( {25 + 75} \right) = 100 + 100 = 200\)
Chu vi và diện tích hình vuông có cạnh là 7 cm lần lượt là
-
A.
\(28\,\,cm;\,\,49\,cm\)
-
B.
\(28\,\,c{m^2};\,\,49\,cm\)
-
C.
\(49\,cm;\,\,28\,\,c{m^2}\)
-
D.
\(28\,\,cm;\,\,49\,c{m^2}\)
Đáp án : D
Chu vi hình vuông cạnh \(a\) là: \(C = 4a\)
Diện tích hình vuông cạnh \(a\) là: \(S = a.a = {a^2}\).
Chu vi hình vuông là: \(4.7 = 28\) (\(cm\))
Diện tích hình vuông là: \({7^2} = 49\,(c{m^2})\)
Tính: \(1 + 12.3.5\)
-
A.
181
-
B.
195
-
C.
180
-
D.
15
Đáp án : A
Thực hiện theo quy tắc:
N hân và chia \( \to \) cộng và trừ.
\(1 + 12.3.5 = 1+\left( {12.3} \right).5 = 1 + 36.5 = 1 + 180 = 181\)
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
Đáp án : A
Sử dụng dấu hiệu nhận biết hình chữ nhật
Hình chữ nhật có bốn đỉnh, hai cặp cạnh đối song song, hai đường chéo bằng nhau.
=> Đáp án B, C, D đúng.
Hình có 4 đỉnh chưa chắc là hình chữ nhật ví dụ:
Các số có chữ số tận cùng là … thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
-
A.
0, 1, 2, 3
-
B.
0, 2, 4, 6, 8
-
C.
1, 3, 5, 7, 9
-
D.
0 hoặc 5
Đáp án : D
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Trong các số 3,5,8,9, số nào thuộc tập hợp \(A = \left\{ {x \in \mathbb{N}\left| {x \ge 8} \right.} \right\}\) , số nào thuộc tập hợp \(B = \left\{ {x \in \mathbb{N}\left| {x < 5} \right.} \right\}\) ?
-
A.
9 thuộc A; 3 và 5 thuộc B
-
B.
9 thuộc A; 3, 5, 8 thuộc B
-
C.
8 và 9 thuộc A; 3 và 5 thuộc B
-
D.
8 và 9 thuộc A; 3 thuộc B.
Đáp án : D
Kí hiệu để nói “ \(a > b\) hoặc \(a = b\) ”
\(A = \left\{ {x \in \mathbb{N}\left| {x \ge 8} \right.} \right\}\) là tập hợp các số lớn hơn 8 và số 8
=> A có 2 phần tử là số 8 và số 9
\(B = \left\{ {x \in \mathbb{N}\left| {x < 5} \right.} \right\} = \left\{ 3 \right\}\)
Vậy 8 và 9 thuộc a; 3 thuộc B.
Tìm số tự nhiên \(n\) biết \({3^n} = 81.\)
-
A.
\(n = 2\)
-
B.
\(n = 4\)
-
C.
\(n = 5\)
-
D.
\(n = 8\)
Đáp án : B
Đưa hai vế về hai lũy thừa cùng số mũ rồi sử dụng \({a^n} = {a^m}\left( {a \ne 0;a \ne 1} \right)\) thì \(n = m.\)
Ta có \({3^n} = 81\) mà \(81 = {3^4}\) nên \({3^n} = {3^4}\) suy ra \(n = 4.\)
Giá trị của biểu thức \(2\left[ {\left( {195 + 35:7} \right):8 + 195} \right] - 400\) bằng
-
A.
$140$
-
B.
$60$
-
C.
$80$
-
D.
$40$
Đáp án : D
Thực hiện phép tính trong ngoặc tròn rồi đến ngoặc vuông. Sau đó là phép nhân và phép trừ.
Ta có \(2\left[ {\left( {195 + 35:7} \right):8 + 195} \right] - 400\)
\( = 2\left[ {\left( {195 + 5} \right):8 + 195} \right] - 400\)
\( = 2\left[ {200:8 + 195} \right] - 400\)
\( = 2\left( {25 + 195} \right) - 400\)
\( = 2.220 - 400\)
\( = 440 - 400\)
\( = 40\)
Tìm số tự nhiên \(x\) biết rằng \(x - 50:25 = 8.\)
-
A.
\(11\)
-
B.
\(250\)
-
C.
\(10\)
-
D.
\(20\)
Đáp án : C
Thực hiện phép chia trước rồi tìm \(x\) bằng cách lấy hiệu cộng với số trừ.
Ta có \(x - 50:25 = 8\)
\(x - 2 = 8\)
\(x = 8 + 2\)
\(x = 10.\)
Số tự nhiên \(x\) nào dưới đây thỏa mãn \({4^x} = {4^3}{.4^5}?\)
-
A.
\(x = 32\)
-
B.
\(x = 16\)
-
C.
\(x = 4\)
-
D.
\(x = 8\)
Đáp án : D
+ Sử dụng công thức ${a^m}.{a^n} = {a^{m + n}}$ để tính vế trái.
+ Sử dụng \({a^n} = {a^m}\left( {a \ne 0;a \ne 1} \right)\) thì \(n = m.\)
Ta có \({4^x} = {4^3}{.4^5}\)
\({4^x} = {4^{3 + 5}}\)
\({4^x} = {4^8}\)
\(x = 8\)
Vậy \(x = 8.\)
Có bao nhiêu giá trị của \(x\) thỏa mãn \(240 - \left[ {23 + \left( {13 + 24.3 - x} \right)} \right] = 132?\)
-
A.
$3$
-
B.
$2$
-
C.
$1$
-
D.
$4$
Đáp án : C
+ Tìm số trừ bằng cách lấy số bị trừ trừ đi hiệu.
+ Tìm số hạng bằng tổng trừ đi số hạng đã biết.
Ta có \(240 - \left[ {23 + \left( {13 + 24.3 - x} \right)} \right] = 132\)
\(23 + \left( {13 + 72 - x} \right) = 240 - 132\)
\(23 + \left( {85 - x} \right) = 108\)
\(85 - x = 108 - 23\)
\(85 - x = 85\)
\(x = 85 - 85\)
\(x = 0.\)
Vậy có một giá trị \(x = 0\) thỏa mãn đề bài.
Dùng ba trong bốn chữ số \(5;8;4;0\) hãy lập ra các số tự nhiên chia hết cho \(3\) mà không chia hết cho \(9.\)
-
A.
\(840;804;408\)
-
B.
\(840;804;408;480\)
-
C.
\(540;450;405\)
-
D.
\(540;450;405;504\)
Đáp án : B
Sử dụng dấu hiệu chia hết cho \(3.\) Ta lập các bộ số có tổng chia hết cho \(3\) mà không chia hết cho \(9.\)
Sau đó tìm ra các số thỏa mãn đề bài từ bộ số tìm được.
Ta thấy chỉ có \(8 + 4 + 0 = 12\) chia hết cho \(3\) nhưng không chia hết cho \(9\) nên các số cần tìm là \(840;480;408;804.\)
Có bao nhiêu số tự nhiên \(x\) khác \(0\) thỏa mãn $x \in BC(12 ; 15 ; 20) $ và $x$ $ \le $ $100$
-
A.
$4$
-
B.
$3$
-
C.
$2$
-
D.
$1$
Đáp án : D
+ Tìm các bội số nhỏ hơn \(100\) của \(12;15;20.\)
+ Tìm các số chung cho cả ba số \(12;15;20\) trong bội số tìm được.
Ta có \(B\left( {12} \right) = \left\{ {0;12;24;36;48;60;72;84;96;...} \right\}\)
\(B\left( {15} \right) = \left\{ {0;15;30;45;60;75;90;105;...} \right\}\)
\(B\left( {20} \right) = \left\{ {0;20;40;60;80;100;...} \right\}\)
Nên \(BC\left( {12;15;20} \right) = \left\{ {0;60;120;...} \right\}\) mà \(x \le 100\) và \(x \ne 0\) nên \(x = 60.\)
Có một số tự nhiên thỏa mãn đề bài.

Độ dài đáy của hình bình hành có chiều cao \(24cm\) và diện tích là \(432c{m^2}\) là:
A. \(16cm\)
B. \(17cm\)
C. \(18cm\)
D. \(19cm\)
C. \(18cm\)
Từ công thức tính diện tích hình bình hành: \(S = a \times h\), ta có thể suy ra công thức tính độ dài cạnh đáy \(a\) là \(a = S:h\).
Độ dài đáy của hình bình hành đó là:
\(432:24 = 18\,\,(cm)\)
Đáp số: \(18cm\).
Một mảnh giấy hình chữ nhật có diện tích \(96 cm^2\). Một cạnh có độ dài 12 cm. Tính chu vi của mảnh giấy đó?
-
A.
8 cm
-
B.
20 cm
-
C.
40 cm
-
D.
80 cm
Đáp án : C
- Tính chiều dài cạnh còn lại của mảnh giấy hình chữ nhật.
=> Chu vi của mảnh giấy.
Chiều dài cạnh còn lại của mảnh giấy hình chữ nhật là: 96 : 12 = 8 (cm)
Chu vi của mảnh giấy là: 2.(8 + 12) = 40 (cm)

Điền số thích hợp vào ô trống:
Từ bốn chữ số $0;{\rm{ 3; 5;}}\,\,9$ có thể viết được
số có ba chữ số khác nhau và chia hết cho \(5\).
Từ bốn chữ số $0;{\rm{ 3; 5;}}\,\,9$ có thể viết được
số có ba chữ số khác nhau và chia hết cho \(5\).
Áp dụng tính chất các số chữ số tận cùng là \(0\) hoặc \(5\) thì chia hết cho \(5\) để viết các số có ba chữ số khác nhau từ bốn chữ số trên mà chia hết cho \(5\).
Ta đếm số lượng các số chia hết cho \(5\) và điền vào ô trống.
Để lập được số chia hết cho \(5\) thì các số đó phải có chữ số tận cùng là \(0\) hoặc \(5\).
Từ bốn chữ số $0;{\rm{ 3; 5;}}\,9$ ta viết được các số có ba chữ số khác nhau và chia hết cho \(5\) là:
\(350\,;\,\,390\,;\,530\,;\,\,590;\,\,930\,;\,\,950;\,\,\,305\,;\,\,395\,;\,\,905\,;935\).
Có \(10\) số có ba chữ số khác nhau và chia hết cho \(5\). Vậy đáp án đúng điền vào ô trống là \(10\).
-
A.
91 m 2
-
B.
18 m 2
-
C.
87 m 2
-
D.
69 m 2
Đáp án : D
Vẽ thêm vào các góc khuyết để tạo thành hình chữ nhật lớn
Diện tích mảnh vườn = Diện tích HCN lớn – (diện tích hình chữ nhật + diện tích hình vuông khuyết)
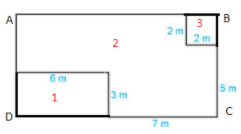
Ta thấy tổng diện tích của hình 1, hình 2, hình 3 bằng tổng diện tích của hình chữ nhật ABCD
Chiều dài DC của hình chữ nhật ABCD là: 7 + 6 = 13 (m)
Chiều rộng của hình chữ nhật ABCD là: 2 + 5 = 7 (m)
Diện tích hình chữ nhật ABCD là: 13.7 = 91 (m 2 )
Hình 1 là hình chữ nhật có chiều dài 6 m và chiều rộng 3 m nên diện tích hình 1 là: 6.3 = 18 (m 2 )
Hình 3 là hình vuông có cạnh bằng 2 m nên diện tích hình 3 là: 2.2 = 4 (m 2 )
Vậy diện tích mảnh vườn bằng cần tìm bằng diện tích hình 2 và bằng:
91 - 18 - 4 = 69 (m 2 )
Một miếng đất hình chữ nhật có chiều dài 64 m, chiều rộng 34 m. Người ta giảm chiều dài và tăng chiều rộng để miếng đất là hình vuông, biết phần diện tích giảm theo chiều dài là 272. Tìm phần diện tích tăng thêm theo chiều rộng.
-
A.
\(176\,{m^2}\)
-
B.
\(2176\,{m^2}\)
-
C.
\(1232\,{m^2}\)
-
D.
\(3136\,{m^2}\)
Đáp án : C
- Tính số đo bị giảm của chiều dài miếng đất
- Tính cạnh của miếng đất hình vuông
- Tính chiều rộng miếng đất được tăng thêm
- Tính diện tích phần tăng theo chiều rộng miếng đất.
Ta có hình vẽ minh họa sau:
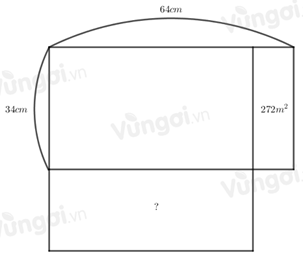
Số đo bị giảm của chiều dài miếng đất là:
272 : 34 = 8 (m)
Cạnh của miếng đất hình vuông là:
64 – 8 = 56 (m)
Chiều rộng miếng đất được tăng thêm số mét là:
56 – 34 = 22 (m)
Diện tích phần tăng theo chiều rộng miếng đất là:
56 . 22 = 1232 (m 2 )
-
A.
9
-
B.
14
-
C.
10
-
D.
13
Đáp án : B
Đếm số hình vuông nhỏ + số hình vuông được ghép từ các ô vuông nhỏ.
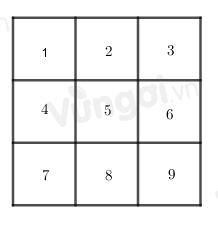
Ta đánh số như hình trên:
+ 9 hình vuông nhỏ là: 1, 2, 3, 4, 5, 6, 7, 8, 9.
+ 4 hình vuông được gép từ bốn hình vuông nhỏ là: 1245, 2356, 4578, 5689.
+ 1 hình vuông lớn được ghép từ 9 hình vuông nhỏ.
Vậy có tất cả \(9 + 4 + 1 = 14\) hình vuông.