Đề kiểm tra giữa học kì 1 Toán 6 Kết nối tri thức - Đề số 3
Đề bài
Kết quả của phép tính \(547.63 + 547.37\) là
-
A.
\(54700\)
-
B.
\(5470\)
-
C.
\(45700\)
-
D.
\(54733\)
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là $0$ .
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung.
Cho \(a \vdots m\) và \(b \vdots m\) và \(c \vdots m\) với m là số tự nhiên khác 0. Các số a,b,c là số tự nhiên tùy ý.
Khẳng định nào sau đây chưa đúng?
(Xét trong tập số tự nhiên, số bị trừ phải lớn hơn hoặc bằng số trừ)
-
A.
\(\left( {a + b} \right) \vdots m\)
-
B.
\(\left( {a - b} \right) \vdots m\)
-
C.
\(\left( {a + b + c} \right) \vdots m\)
-
D.
\(\left( {b + c} \right) \vdots m\)

Các số không chia hết cho \(5\) có chữ số tận cùng là:
A. \(1\,;\,\,2\,;\,\,3\,;\,\,4\)
B. \(6\,;\,\,7\)
C. \(8\,;\,\,9\)
D. Tất cả các đáp án trên đều đúng
Kết quả của phép tính $12.100 + 100.36 - 100.19$ là
-
A.
\(29000\)
-
B.
\(3800\)
-
C.
\(290\)
-
D.
\(2900\)
Chọn câu sai.
-
A.
\({5^3} < {3^5}\)
-
B.
\({3^4} > {2^5}\)
-
C.
\({4^3} = {2^6}\)
-
D.
\({4^3} > {8^2}\)
Tính: \(1 + 12.3.5\)
-
A.
181
-
B.
195
-
C.
180
-
D.
15
Khẳng định nào là sai:
-
A.
$0$ và $1$ không là số nguyên tố cũng không phải hợp số.
-
B.
Cho số $a > 1$, $a$ có $2$ ước thì $a$ là hợp số.
-
C.
$2$ là số nguyên tố chẵn duy nhất.
-
D.
Số nguyên tố là số tự nhiên lớn hơn $1$ mà chỉ có hai ước là $1$ và chính nó.
Tính giá trị của lũy thừa \({2^6},\) ta được
-
A.
\(32\)
-
B.
\(64\)
-
C.
\(16\)
-
D.
\(128\)
Phân tích số $18$ thành thừa số nguyên tố:
-
A.
$18 = 18.1$
-
B.
$18 = 10 + 8$
-
C.
$18 = {2.3^2}$
-
D.
$18 = 6 + 6 + 6$
-
A.
20 cm 2
-
B.
25 cm
-
C.
20 cm
-
D.
10 cm
 \((a + b) + c = a + (b + c)\). Đúng hay sai?
\((a + b) + c = a + (b + c)\). Đúng hay sai?
-
A.
EF là đường chéo
-
B.
EF và GH là đường chéo
-
C.
EH và FG là đường chéo
-
D.
EG và HF là đường chéo
-
A.
\(MN\) và \(PQ\) song song
-
B.
\(MN\) và \(NP\) song song
-
C.
\(MQ\) và \(PQ\) song song
-
D.
\(MN\) và \(MQ\) song song
Thay dấu * để được số nguyên tố $\overline {*1} $:
-
A.
$2$
-
B.
$8$
-
C.
$5$
-
D.
$4$
Chọn câu đúng:
-
A.
Chu vi của một hình bình hành bằng tổng một cặp cạnh kề nhau bất kỳ.
-
B.
Chu vi hình bình hành bằng tổng của cạnh đáy và chiều cao.
-
C.
Chu vi hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
-
D.
Chu vi của một hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.
Cho \(\overline {1a52} \) chia hết cho 9. Số thay thế cho \(a\) có thể là
-
A.
1
-
B.
2
-
C.
3
-
D.
5

Trong các hình sau, hình nào là hình thoi?
A.
B.
C.

D.

Viết tập hợp \(A = \left\{ {16;17;18;19} \right\}\) dưới dạng chỉ ra tính chất đặc trưng.
-
A.
\(A = \left\{ {x \in N|15 < x < 19} \right\}\)
-
B.
\(A = \left\{ {x\in N |15 < x < 20} \right\}\)
-
C.
\(A = \left\{ {x\in N |16 < x < 20} \right\}\)
-
D.
\(A = \left\{ {x\in N |15 < x \le 20} \right\}\)
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là 0
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung
Số $x$ là bội chung của ${\rm{a;b;c}}$ nếu:
-
A.
$x \, \vdots \, a$ hoặc $x \, \vdots \, b$ hoặc $x \, \vdots \, c$
-
B.
$x \, \vdots \, a$ và $x \, \vdots \, b$
-
C.
$x \, \vdots \, b$ và $x \, \vdots \, c$
-
D.
$x \, \vdots \, a$ và $x \, \vdots \, b$ và $x \, \vdots \, c$
Hãy chọn câu sai:
-
A.
Số chia hết cho 2 và 5 có tận cùng là số 0
-
B.
Một số chia hết cho 10 thì số đó chia hết cho 2
-
C.
Số chia hết cho 2 thì có tận cùng là số lẻ
-
D.
Số dư trong phép chia một số cho 2 bằng số dư trong phép chia chữ số tận cùng của nó cho 2
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
Sau khi phân tích 45, 150 ra các thừa số nguyên tố được 45 = 3 2 .5 và 150 = 2.3.5 2 . Số mũ nhỏ nhất của thừa số chung 3 là
-
A.
1
-
B.
2
-
C.
3
-
D.
0
Chọn câu đúng:
-
A.
Diện tích hình bình hành bằng nửa tích của cạnh đáy nhân với chiều cao.
-
B.
Diện tích hình bình hành bằng tổng của cạnh đáy và chiều cao.
-
C.
Diện tích hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
-
D.
Diện tích hình bình hành bằng hiệu của cạnh đáy và chiều cao.
Năm 2000 là thế kỉ bao nhiêu?
-
A.
XX
-
B.
XIX
-
C.
XXI
-
D.
XXX
-
A.
Góc E
-
B.
Góc F
-
C.
Góc G
-
D.
Góc O
Nếu hình thoi có độ dài 1 cạnh là a thì:
-
A.
Chu vi của hình thoi là 4a
-
B.
Chu vi của hình thoi là 6a
-
C.
Chu vi của hình thoi là a 2
-
D.
Chu vi của hình thoi là a + b + c trong đó b và c là độ dài hai đường chéo.
Số tự nhiên \(x\) thỏa mãn \({\left( {2x + 1} \right)^3} = 125\) là
-
A.
\(x = 2\)
-
B.
\(x = 3\)
-
C.
\(x = 5\)
-
D.
\(x = 4\)
Dùng ba trong bốn chữ số \(5;8;4;0\) hãy lập ra các số tự nhiên chia hết cho \(3\) mà không chia hết cho \(9.\)
-
A.
\(840;804;408\)
-
B.
\(840;804;408;480\)
-
C.
\(540;450;405\)
-
D.
\(540;450;405;504\)
Tìm các ước chung của \(18;30;42.\)
-
A.
\(\left\{ {2;3;6} \right\}\)
-
B.
\(\left\{ {1;2;3;6} \right\}\)
-
C.
\(\left\{ {1;2;3} \right\}\)
-
D.
\(\left\{ {1;2;3;6;9} \right\}\)
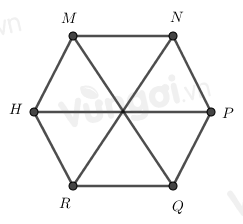
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
-
A.
8
-
B.
2
-
C.
4
-
D.
6
Chọn đáp án đúng hoặc sai cho mỗi khẳng định bên dưới:
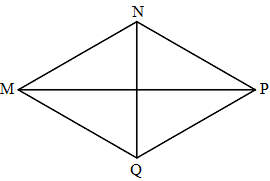
Trong hình thoi MNPQ:
MN và PQ không bằng nhau.
MN không song song với MQ
Các cặp cạnh đối diện song song.
MN = NP = PQ = QM
Một hình thang có diện tích 20 m 2 , đáy lớn 55dm và đáy bé 45dm. Tính chiều cao của hình thang?
-
A.
2 dm
-
B.
4 dm
-
C.
40 dm
-
D.
20 dm

Điền số thích hợp vào ô trống:
Từ bốn chữ số $0;{\rm{ 3; 5;}}\,\,9$ có thể viết được
số có ba chữ số khác nhau và chia hết cho \(5\).
Tính diện tích của hình thoi có tổng độ dài hai đường chéo là 30cm và đường chéo lớn hơn đường chéo bé 2cm.
-
A.
110 cm 2
-
B.
112 cm 2
-
C.
111 cm 2
-
D.
114 cm 2
Một mảnh giấy hình chữ nhật có diện tích \(96 cm^2\). Một cạnh có độ dài 12 cm. Tính chu vi của mảnh giấy đó?
-
A.
8 cm
-
B.
20 cm
-
C.
40 cm
-
D.
80 cm
Tìm số \(\overline {xy} \) biết \(\overline {xy} .\overline {xyx} = \overline {xyxy} \)
-
A.
\(10\)
-
B.
\(11\)
-
C.
\(12\)
-
D.
\(13\)
Cho hình bình hành có chu vi là 480cm, có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
-
A.
5000 cm
-
B.
10000 cm
-
C.
2500 cm 2
-
D.
5000 cm 2
Cho \(A = 3 + {3^2} + {3^3} + ... + {3^{100}}\) . Tìm số tự nhiên \(n\) biết rằng \(2A + 3 = {3^n}.\)
-
A.
\(n = 99\)
-
B.
\(n = 100\)
-
C.
\(n = 101\)
-
D.
\(n = 102\)
Lời giải và đáp án
Kết quả của phép tính \(547.63 + 547.37\) là
-
A.
\(54700\)
-
B.
\(5470\)
-
C.
\(45700\)
-
D.
\(54733\)
Đáp án : A
Sử dụng tính chất phân phối của phép nhân đối với phép cộng để thực hiện phép tính.
$ab+ac=a(b+c)$
Ta có \(547.63 + 547.37\)\( = 547.\left( {63 + 37} \right) = 547.100 = 54700.\)
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là $0$ .
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung.
Đáp án : A
- Áp dụng kiến thức:
Mọi số tự nhiên đều có ước là $1$.
Số nguyên tố có $2$ ước là $1$ và chính nó.
Mọi số nguyên tố khác nhau đều có ước chung duy nhất là $1$.
A. Đáp án này đúng vì mọi số tự nhiên đều có ước chung là $1$.
B. Đáp án này sai, vì $0$ không là ước của $1$ số nào cả.
C. Đáp án này sai, vì số nguyên tố có $2$ ước là $1$ và chính nó.
D. Đáp án này sai, vì $2$ số nguyên tố có ước chung là $1$.
Cho \(a \vdots m\) và \(b \vdots m\) và \(c \vdots m\) với m là số tự nhiên khác 0. Các số a,b,c là số tự nhiên tùy ý.
Khẳng định nào sau đây chưa đúng?
(Xét trong tập số tự nhiên, số bị trừ phải lớn hơn hoặc bằng số trừ)
-
A.
\(\left( {a + b} \right) \vdots m\)
-
B.
\(\left( {a - b} \right) \vdots m\)
-
C.
\(\left( {a + b + c} \right) \vdots m\)
-
D.
\(\left( {b + c} \right) \vdots m\)
Đáp án : B
Tính chất 1 : Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
\(a \vdots m\) và \(b \vdots m\) \( \Rightarrow \left( {a + b} \right) \vdots m\)
\(a \vdots m\) và \(b \vdots m\) \( \Rightarrow \left( {a - b} \right) \vdots m\) với \(\left( {a \ge b} \right)\)
\(a \vdots m;b \vdots m;c \vdots m \Rightarrow \left( {a + b + c} \right) \vdots m\)
\(\left( {a - b} \right) \vdots m\) sai vì thiếu điều kiện \(a \ge b\)

Các số không chia hết cho \(5\) có chữ số tận cùng là:
A. \(1\,;\,\,2\,;\,\,3\,;\,\,4\)
B. \(6\,;\,\,7\)
C. \(8\,;\,\,9\)
D. Tất cả các đáp án trên đều đúng
D. Tất cả các đáp án trên đều đúng
Các số không có chữ số tận cùng là \(0\) hoặc \(5\) thì không chia hết cho \(5\).
Do đó các số không chia hết cho \(5\) có chữ số tận cùng là \(1\,;\,\,2\,;\,\,3\,;\,\,4;\,\,6\,;\,\,7\,;\,\,8\,;\,\,9\).
Vậy tất cả các đáp án A, B, C đều đúng.
Kết quả của phép tính $12.100 + 100.36 - 100.19$ là
-
A.
\(29000\)
-
B.
\(3800\)
-
C.
\(290\)
-
D.
\(2900\)
Đáp án : D
Sử dụng tính chất phân phối của phép nhân với phép cộng; phép trừ \(ab + ac - ad = a\left( {b + d - c} \right).\)
Ta có $12.100 + 100.36 - 100.19$\( = 100.\left( {12 + 36 - 19} \right) = 100.29 = 2900.\)
Chọn câu sai.
-
A.
\({5^3} < {3^5}\)
-
B.
\({3^4} > {2^5}\)
-
C.
\({4^3} = {2^6}\)
-
D.
\({4^3} > {8^2}\)
Đáp án : D
So sánh các lũy thừa bằng cách tính giá trị rồi so sánh.
Cách giải:
+) Ta có \({5^3} = 5.5.5 = 125\); \({3^5} = 3.3.3.3.3 = 243\) nên \({5^3} < {3^5}\) ( A đúng)
+) \({3^4} = 3.3.3.3 = 81\) và \({2^5} = 2.2.2.2.2 = 32\) nên \({3^4} > {2^5}\) ( B đúng)
+) \({4^3} = 4.4.4 = 64\) và \({2^6} = 2.2.2.2.2.2 = 64\) nên \({4^3} = {2^6}\) ( C đúng)
+) \({4^3} = 64;{8^2} = 64\) nên \({4^3} = {8^2}\) ( D sai)
Tính: \(1 + 12.3.5\)
-
A.
181
-
B.
195
-
C.
180
-
D.
15
Đáp án : A
Thực hiện theo quy tắc:
N hân và chia \( \to \) cộng và trừ.
\(1 + 12.3.5 = 1+\left( {12.3} \right).5 = 1 + 36.5 = 1 + 180 = 181\)
Khẳng định nào là sai:
-
A.
$0$ và $1$ không là số nguyên tố cũng không phải hợp số.
-
B.
Cho số $a > 1$, $a$ có $2$ ước thì $a$ là hợp số.
-
C.
$2$ là số nguyên tố chẵn duy nhất.
-
D.
Số nguyên tố là số tự nhiên lớn hơn $1$ mà chỉ có hai ước là $1$ và chính nó.
Đáp án : B
Áp dụng định nghĩa:
+ Hợp số là một số tự nhiên có thể biểu diễn thành tích của hai số tự nhiên khác nhỏ hơn nó. Một định nghĩa khác tương đương: hợp số là số chia hết cho các số khác ngoài 1 và chính nó.
+ Số nguyên tố là số tự nhiên lớn hơn $1$ mà chỉ có hai ước là $1$ và chính nó.
+) Số $a$ phải là số tự nhiên lớn hơn \(1\) và có nhiều hơn $2$ ước thì $a$ mới là hợp số nên B sai.
+) $1$ là số tự nhiên chỉ có $1$ ước là $1$ nên không là số nguyên tố và $0$ là số tự nhiên nhỏ hơn $1$ nên không là số nguyên tố. Lại có $0$ và $1$ đều không là hợp số do đó A đúng.
+) Số nguyên tố là số tự nhiên lớn hơn $1$ mà chỉ có hai ước là $1$ và chính nó nên D đúng và suy ra $2$ là số nguyên tố chẵn duy nhất nên C đúng.
Tính giá trị của lũy thừa \({2^6},\) ta được
-
A.
\(32\)
-
B.
\(64\)
-
C.
\(16\)
-
D.
\(128\)
Đáp án : B
Sử dụng công thức \({a^n} = a.a.a...a\) (\(n\) thừa số $a$) để tính giá trị.
Ta có \({2^6} = 2.2.2.2.2.2 = 4.4.4 = 16.4 = 64.\)
Phân tích số $18$ thành thừa số nguyên tố:
-
A.
$18 = 18.1$
-
B.
$18 = 10 + 8$
-
C.
$18 = {2.3^2}$
-
D.
$18 = 6 + 6 + 6$
Đáp án : C
- Phân tích số ra thành số nguyên tố.
- Đáp án A sai vì 1 không phải là số nguyên tố
- Đáp án B sai vì đây là phép cộng.
- Đáp án C đúng vì $2$ và $3$ là $2$ số nguyên tố và ${2.3^2} = 2.9 = 18$
- Đáp án D sai vì đây là phép cộng.
-
A.
20 cm 2
-
B.
25 cm
-
C.
20 cm
-
D.
10 cm
Đáp án : C
Chu vi hình thoi MPNQ là: 4.5 = 20 (cm)
 \((a + b) + c = a + (b + c)\). Đúng hay sai?
\((a + b) + c = a + (b + c)\). Đúng hay sai?
Khi cộng một tổng hai số với số thứ ba, ta có thể cộng số thứ nhất với tổng của số thứ hai và số thứ ba.
Do đó ta có: $\left( {a + b} \right) + c{\rm{ }} = {\rm{ }}a + \left( {b + c} \right)$.
Vậy khẳng định đã cho là đúng.
-
A.
EF là đường chéo
-
B.
EF và GH là đường chéo
-
C.
EH và FG là đường chéo
-
D.
EG và HF là đường chéo
Đáp án : D
Sử dụng dấu hiệu nhận biết hình thang cân.
Hình thang cân EFGH có: EG và HF là đường chéo.
-
A.
\(MN\) và \(PQ\) song song
-
B.
\(MN\) và \(NP\) song song
-
C.
\(MQ\) và \(PQ\) song song
-
D.
\(MN\) và \(MQ\) song song
Đáp án : A
Trong hình vuông, hai cặp cạnh đối song song với nhau.
Trong hình vuông \(MNPQ\) có hai cặp cạnh đối song song với nhau là:
+ \(MN\) và \(PQ\).
+ \(MQ\) và \(NP\)
=> Đáp án A đúng .
Thay dấu * để được số nguyên tố $\overline {*1} $:
-
A.
$2$
-
B.
$8$
-
C.
$5$
-
D.
$4$
Đáp án : D
+ Dấu * có thể nhận các giá trị \(\left\{ {2;8;5;4} \right\}\)
+ Dùng định nghĩa số nguyên tố để tìm ra số nguyên tố
Dấu * có thể nhận các giá trị \(\left\{ {2;8;5;4} \right\}\)
+) Ta có \(21\) có các ước \(1;3;7;21\) nên \(21\) là hợp số. Loại A
+) \(81\) có các ước \(1;3;9;27;81\) nên \(81\) là hợp số. Loại B
+) \(51\) có các ước \(1;3;17;51\) nên \(51\) là hợp số. Loại C
+) \(41\) chỉ có hai ước là \(1;41\) nên \(41\) là số nguyên tố.
Chọn câu đúng:
-
A.
Chu vi của một hình bình hành bằng tổng một cặp cạnh kề nhau bất kỳ.
-
B.
Chu vi hình bình hành bằng tổng của cạnh đáy và chiều cao.
-
C.
Chu vi hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
-
D.
Chu vi của một hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.
Đáp án : D
Sử dụng công thức tính chu vi hình bình hành.
Chu vi của một hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.
Cho \(\overline {1a52} \) chia hết cho 9. Số thay thế cho \(a\) có thể là
-
A.
1
-
B.
2
-
C.
3
-
D.
5
Đáp án : A
Tìm điều kiện của \(a\).
Tính tổng các chữ số trong \(\overline {1a52} \)
Tìm \(a\) để tổng đó chia hết cho 9.
Tổng các chữ số của \(\overline {1a52} \) là \(1 + a + 5 + 2 = a + 8\) để số \(\overline {1a52} \) chia hết cho 9 thì \(a + 8\) phải chia hết cho 9.
Do a là các số tự nhiên từ 0 đến 9 nên
\(\begin{array}{l}0 + 8 \le a + 8 \le 9 + 8\\ \Rightarrow 8 \le a + 8 \le 17\end{array}\)
Số chia hết cho 9 từ 8 đến 17 chỉ có đúng một số 9, do đó \(a + 8 = 9 \Rightarrow a = 1\)
Vậy số thay thế cho a chỉ có thể là 1

Trong các hình sau, hình nào là hình thoi?
A.

B.

C.

D.

B.

Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Quan sát các hình đã cho ta thấy hình A là hình thang, hình B là hình thoi, hình C là hình tròn, hình D là hình bình hành.
Vậy trong các hình đã cho, hình B là hình thoi.
Viết tập hợp \(A = \left\{ {16;17;18;19} \right\}\) dưới dạng chỉ ra tính chất đặc trưng.
-
A.
\(A = \left\{ {x \in N|15 < x < 19} \right\}\)
-
B.
\(A = \left\{ {x\in N |15 < x < 20} \right\}\)
-
C.
\(A = \left\{ {x\in N |16 < x < 20} \right\}\)
-
D.
\(A = \left\{ {x\in N |15 < x \le 20} \right\}\)
Đáp án : B
+ Tìm tính chất chung của các phần tử trong tập hợp
+ Viết tập hợp dưới dạng chỉ ra tính chất đặc trưng
Nhận thấy các số \(16;17;18;19\) là các số tự nhiên lớn hơn \(15\) và nhỏ hơn \(20\)
Nên \(A = \left\{ {x \in N |15 < x < 20} \right\}\).
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là 0
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung
Đáp án : A
- Áp dụng kiến thức:
Mọi số tự nhiên đều có ước là $1$.
Số nguyên tố có $2$ ước là $1$ và chính nó.
Mọi số nguyên tố khác nhau đều có ước chung duy nhất là $1$.
A. Đáp án này đúng vì mọi số tự nhiên đều có ước chung là $1$
B. Đáp án này sai, vì $0$ không là ước của $1$ số nào cả.
C. Đáp án này sai, vì số nguyên tố có $2$ ước là $1$ và chính nó.
D. Đáp án này sai, vì $2$ số nguyên tố có ước chung là $1$.
Số $x$ là bội chung của ${\rm{a;b;c}}$ nếu:
-
A.
$x \, \vdots \, a$ hoặc $x \, \vdots \, b$ hoặc $x \, \vdots \, c$
-
B.
$x \, \vdots \, a$ và $x \, \vdots \, b$
-
C.
$x \, \vdots \, b$ và $x \, \vdots \, c$
-
D.
$x \, \vdots \, a$ và $x \, \vdots \, b$ và $x \, \vdots \, c$
Đáp án : D
- Sử dụng kiến thức bội chung $2$ hay nhiều số: bội chung của $2$ hay nhiều số là bội của tất cả các số đó.
Số \(x\) là bội chung của $3$ số $a,b,c$ nếu \(x\) chia hết cho cả \(a,b,c\).
Hãy chọn câu sai:
-
A.
Số chia hết cho 2 và 5 có tận cùng là số 0
-
B.
Một số chia hết cho 10 thì số đó chia hết cho 2
-
C.
Số chia hết cho 2 thì có tận cùng là số lẻ
-
D.
Số dư trong phép chia một số cho 2 bằng số dư trong phép chia chữ số tận cùng của nó cho 2
Đáp án : C
Số chia hết cho $2$ có tận cùng là số chẵn nên câu sai là: Số chia hết cho 2 có tận cùng là số lẻ.
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
Đáp án : A
Sử dụng dấu hiệu nhận biết hình chữ nhật
Hình chữ nhật có bốn đỉnh, hai cặp cạnh đối song song, hai đường chéo bằng nhau.
=> Đáp án B, C, D đúng.
Hình có 4 đỉnh chưa chắc là hình chữ nhật ví dụ:
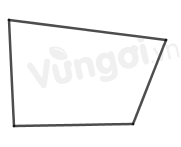
Sau khi phân tích 45, 150 ra các thừa số nguyên tố được 45 = 3 2 .5 và 150 = 2.3.5 2 . Số mũ nhỏ nhất của thừa số chung 3 là
-
A.
1
-
B.
2
-
C.
3
-
D.
0
Đáp án : A
Xác định số mũ của thừa số 3 trong hai số 45 và 150.
Chọn ra số nhỏ nhất làm số mũ nhỏ nhất.
45 = 3 2 .5 nên số mũ của 3 là 2
150 = 2.3.5 2 nên số mũ của 3 là 1
Số nhỏ nhất là 1 nên số mũ nhỏ nhất của thừa số chung 3 khi phân tích 45 và 150 ra tích các thừa số nguyên tố là 1.
Chọn câu đúng:
-
A.
Diện tích hình bình hành bằng nửa tích của cạnh đáy nhân với chiều cao.
-
B.
Diện tích hình bình hành bằng tổng của cạnh đáy và chiều cao.
-
C.
Diện tích hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
-
D.
Diện tích hình bình hành bằng hiệu của cạnh đáy và chiều cao.
Đáp án : C
Diện tích hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
Năm 2000 là thế kỉ bao nhiêu?
-
A.
XX
-
B.
XIX
-
C.
XXI
-
D.
XXX
Đáp án : A
Cứ 100 năm là 1 thế kỉ.
Thế kỉ I bắt đầu từ ngày 1 tháng 1 năm 1 và kết thúc vào ngày 31 tháng 12 năm 100.
Năm cuối cùng của thế kỉ XX là 2000.
Năm 2000 là thế kỉ XX.
-
A.
Góc E
-
B.
Góc F
-
C.
Góc G
-
D.
Góc O
Đáp án : C
Sử dụng: Hai góc kề một cạnh bên của hình thang cân bằng nhau.
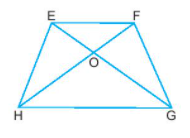
Do góc H và góc G cùng kề đáy HG của hình thang EFGH nên:
Góc H bằng góc G.
Nếu hình thoi có độ dài 1 cạnh là a thì:
-
A.
Chu vi của hình thoi là 4a
-
B.
Chu vi của hình thoi là 6a
-
C.
Chu vi của hình thoi là a 2
-
D.
Chu vi của hình thoi là a + b + c trong đó b và c là độ dài hai đường chéo.
Đáp án : A
Nếu hình thoi có độ dài 1 cạnh là a thì chu vi của hình thoi là 4a.
Số tự nhiên \(x\) thỏa mãn \({\left( {2x + 1} \right)^3} = 125\) là
-
A.
\(x = 2\)
-
B.
\(x = 3\)
-
C.
\(x = 5\)
-
D.
\(x = 4\)
Đáp án : A
Đưa về hai lũy thừa cùng số mũ rồi cho hai cơ số bằng nhau.
Ta có \({\left( {2x + 1} \right)^3} = 125\)
\({\left( {2x + 1} \right)^3} = {5^3}\)
\(2x + 1 = 5\)
\(2x = 5 - 1\)
\(2x = 4\)
\(x = 4:2\)
\(x = 2.\)
Dùng ba trong bốn chữ số \(5;8;4;0\) hãy lập ra các số tự nhiên chia hết cho \(3\) mà không chia hết cho \(9.\)
-
A.
\(840;804;408\)
-
B.
\(840;804;408;480\)
-
C.
\(540;450;405\)
-
D.
\(540;450;405;504\)
Đáp án : B
Sử dụng dấu hiệu chia hết cho \(3.\) Ta lập các bộ số có tổng chia hết cho \(3\) mà không chia hết cho \(9.\)
Sau đó tìm ra các số thỏa mãn đề bài từ bộ số tìm được.
Ta thấy chỉ có \(8 + 4 + 0 = 12\) chia hết cho \(3\) nhưng không chia hết cho \(9\) nên các số cần tìm là \(840;480;408;804.\)
Tìm các ước chung của \(18;30;42.\)
-
A.
\(\left\{ {2;3;6} \right\}\)
-
B.
\(\left\{ {1;2;3;6} \right\}\)
-
C.
\(\left\{ {1;2;3} \right\}\)
-
D.
\(\left\{ {1;2;3;6;9} \right\}\)
Đáp án : B
+ Tìm các ước của \(18;30;42.\)
+ Tìm các số là ước của cả ba số \(18;30;42.\)
+) Ư\(\left( {18} \right) = \left\{ {1;2;3;6;9;18} \right\}\)
+) Ư\(\left( {30} \right) = \left\{ {1;2;3;5;6;10;15;30} \right\}\)
+) Ư\(\left( {42} \right) = \left\{ {1;2;3;6;7;12;14;21;42} \right\}\)
Nên ƯC\(\left( {18;30;42} \right) = \left\{ {1;2;3;6} \right\}\)
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều

-
A.
8
-
B.
2
-
C.
4
-
D.
6
Đáp án : D
Đếm số tam giác đều đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
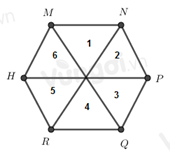
Ta đánh số như hình trên
Nhận thấy có các hình tam giác đều là: 1, 2, 3, 4, 5, 6.
Vậy có 6 tam giác đều.
Chọn đáp án đúng hoặc sai cho mỗi khẳng định bên dưới:

Trong hình thoi MNPQ:
MN và PQ không bằng nhau.
MN không song song với MQ
Các cặp cạnh đối diện song song.
MN = NP = PQ = QM
MN và PQ không bằng nhau.
MN không song song với MQ
Các cặp cạnh đối diện song song.
MN = NP = PQ = QM
Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Trong hình thoi MNPQ ta có:
- Hai cặp cạnh đối diện song song: MN song song với PQ, NP song song với MQ.
- Bốn cạnh bằng nhau: MN = NP = PQ = QM.
Vậy các khẳng định đúng là b,c, d; khẳng định sai là a.
Một hình thang có diện tích 20 m 2 , đáy lớn 55dm và đáy bé 45dm. Tính chiều cao của hình thang?
-
A.
2 dm
-
B.
4 dm
-
C.
40 dm
-
D.
20 dm
Đáp án : C
- Đổi các dữ kiện ra cùng đơn vị đo.
- Gọi đáy lớn, đáy nhỏ, chiều cao, diện tích của hình thang lần lượt là:\( a; b; h; S.\)
\(S = \dfrac{{(a + b).h}}{2} \Rightarrow h = 2.S:\left( {a + b} \right)\)
Đổi \(20\,{m^2} = 2000\,\,d{m^2}\)
Chiều cao của hình thang là:
\(2.2000:(55 + 45) = 40\,(dm)\)

Điền số thích hợp vào ô trống:
Từ bốn chữ số $0;{\rm{ 3; 5;}}\,\,9$ có thể viết được
số có ba chữ số khác nhau và chia hết cho \(5\).
Từ bốn chữ số $0;{\rm{ 3; 5;}}\,\,9$ có thể viết được
số có ba chữ số khác nhau và chia hết cho \(5\).
Áp dụng tính chất các số chữ số tận cùng là \(0\) hoặc \(5\) thì chia hết cho \(5\) để viết các số có ba chữ số khác nhau từ bốn chữ số trên mà chia hết cho \(5\).
Ta đếm số lượng các số chia hết cho \(5\) và điền vào ô trống.
Để lập được số chia hết cho \(5\) thì các số đó phải có chữ số tận cùng là \(0\) hoặc \(5\).
Từ bốn chữ số $0;{\rm{ 3; 5;}}\,9$ ta viết được các số có ba chữ số khác nhau và chia hết cho \(5\) là:
\(350\,;\,\,390\,;\,530\,;\,\,590;\,\,930\,;\,\,950;\,\,\,305\,;\,\,395\,;\,\,905\,;935\).
Có \(10\) số có ba chữ số khác nhau và chia hết cho \(5\). Vậy đáp án đúng điền vào ô trống là \(10\).
Tính diện tích của hình thoi có tổng độ dài hai đường chéo là 30cm và đường chéo lớn hơn đường chéo bé 2cm.
-
A.
110 cm 2
-
B.
112 cm 2
-
C.
111 cm 2
-
D.
114 cm 2
Đáp án : B
- Độ dài đường chéo lớn = (Tổng độ dài hai đường chéo + Hiệu độ dài hai đường chéo) : 2
=> Độ dài đường chéo bé = Tổng độ dài hai đường chéo - Độ dài đường chéo lớn
- Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\).
Độ dài đường chéo lớn là: \(\left( {30 + 2} \right):2 = 16\,\left( {cm} \right)\)
Độ dài đường chéo bé là: \(30 - 16 = 14\left( {cm} \right)\)
Diện tích hình thoi là: \(\frac{{16.14}}{2} = 112\left( {c{m^2}} \right)\)
Một mảnh giấy hình chữ nhật có diện tích \(96 cm^2\). Một cạnh có độ dài 12 cm. Tính chu vi của mảnh giấy đó?
-
A.
8 cm
-
B.
20 cm
-
C.
40 cm
-
D.
80 cm
Đáp án : C
- Tính chiều dài cạnh còn lại của mảnh giấy hình chữ nhật.
=> Chu vi của mảnh giấy.
Chiều dài cạnh còn lại của mảnh giấy hình chữ nhật là: 96 : 12 = 8 (cm)
Chu vi của mảnh giấy là: 2.(8 + 12) = 40 (cm)
Tìm số \(\overline {xy} \) biết \(\overline {xy} .\overline {xyx} = \overline {xyxy} \)
-
A.
\(10\)
-
B.
\(11\)
-
C.
\(12\)
-
D.
\(13\)
Đáp án : A
Sử dụng mối quan hệ giữa các hàng trăm, hàng chục hàng đơn vị khi phân tích một số trong hệ thập phân
Ta có \(\overline {xy} .\overline {xyx} = \overline {xyxy} \)
\(\overline {xy} .\overline {xyx} = \overline {xy} .100 + \overline {xy} \)
\(\overline {xy} .\overline {xyx} = \overline {xy} \left( {100 + 1} \right)\)
\(\overline {xy} .\overline {xyx} = \overline {xy} .101\)
Suy ra \(\overline {xyx} = 101\) nên \(x = 1;y = 0\)
Vậy \(\overline {xy} = 10.\)
Cho hình bình hành có chu vi là 480cm, có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
-
A.
5000 cm
-
B.
10000 cm
-
C.
2500 cm 2
-
D.
5000 cm 2
Đáp án : D
- Tính nửa chu vi hình bình hành
- Tính cạnh đáy của hình bình hành
- Tính chiều cao của hình bình hành
=> Diện tích hình bình hành
Diện tích hình bình hành là: \(S = b.h\)
Trong đó \(b\) là cạnh, \(h\) là chiều cao tương ứng.
- Ta có nửa chu vi hình bình hành là: 480 : 2 = 240 (cm)
Cạnh đáy gấp 5 lần cạnh kia nên nửa chu vi sẽ gấp 6 lần cạnh kia.
- Ta có cạnh đáy hình bình hành là: 240 : 6 . 5 = 200 (cm)
- Chiều cao của hình bình hành là: 200 : 8 = 25 (cm)
- Diện tích của hình bình hành là: 200 . 25 = 5000 (cm 2 )
Cho \(A = 3 + {3^2} + {3^3} + ... + {3^{100}}\) . Tìm số tự nhiên \(n\) biết rằng \(2A + 3 = {3^n}.\)
-
A.
\(n = 99\)
-
B.
\(n = 100\)
-
C.
\(n = 101\)
-
D.
\(n = 102\)
Đáp án : C
+ Tính \(3A\) sau đó tính \(2A = 3A - A\)
+ Sử dụng điều kiện ở đề bài để đưa về dạng hai lũy thừa cùng cơ số. Cho hai số mũ bằng nhau ta tìm được \(n.\)
Ta có \(A = 3 + {3^2} + {3^3} + ... + {3^{100}}\,\,\left( 1 \right)\) nên \(3A = {3^2} + {3^3} + {3^4} + ... + {3^{100}} + {3^{101}}\,\,\left( 2 \right)\)
Lấy \(\left( 2 \right)\) trừ \(\left( 1 \right)\) ta được \(2A = {3^{101}} - 3\) do đó \(2A + 3 = {3^{101}}\) mà theo đề bài \(2A + 3 = {3^n}\)
Suy ra \({3^n} = {3^{101}}\) nên \(n = 101.\)