Đề kiểm tra học kì 1 Toán 6 Kết nối tri thức - Đề số 1
Đề bài
\(a+b\) bằng?
-
A.
\(a+a\)
-
B.
\(b+b\)
-
C.
\(b+a\)
-
D.
\(a\)
Có bao nhiêu ước của \( - 24.\)
-
A.
$9$
-
B.
$17$
-
C.
$8$
-
D.
$16$
Với ba chữ số \(0;1;3\) có thể viết được bao nhiêu số có ba chữ số khác nhau?
-
A.
\(4\)
-
B.
\(3\)
-
C.
\(5\)
-
D.
\(6\)
Tổng \((a+b)+c\) hay \(a+(b+c)\) được gọi là tổng của ... và viết gọn là \(a+b+c\).
-
A.
kết hợp
-
B.
ba số \(a,b,c\)
-
C.
hai số \(a,b\)
-
D.
giao hoán
-
A.
Phép cộng của 1 và 2
-
B.
Phép trừ của 3 và 2
-
C.
Phép cộng của 1 và 3
-
D.
Phép trừ của 3 và 1
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
Viết số 24 bằng số La Mã
-
A.
XXIIII
-
B.
XXIX
-
C.
XXIV
-
D.
XIV
Tập hợp số tự nhiên được kí hiệu là
-
A.
\(N\)
-
B.
\({N^*}\)
-
C.
\(\left\{ N \right\}\)
-
D.
\(Z\)
Số nào trong các số sau không là số nguyên tố?
-
A.
2
-
B.
3
-
C.
5
-
D.
9

Viết số chẵn thích hợp vào chỗ trống:
\(550;\,552;\,554;\)
\(;\)
\(;560.\)
+) Tích của một số chẵn các số nguyên âm là một số nguyên ..(1)..
+) Tích của một số lẻ các số nguyên âm là một số nguyên ..(2)..
Từ thích hợp để điền vào hai chỗ chấm trên lần lượt là:
-
A.
âm, dương
-
B.
dương, âm
-
C.
âm, âm
-
D.
dương, dương
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là $0$ .
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung.
BCNN(10, 15, 30) là:
-
A.
10
-
B.
15
-
C.
30
-
D.
60
Chọn câu sai.
-
A.
\(\left( { - 19} \right).\left( { - 7} \right) > 0\)
-
B.
\(3.\left( { - 121} \right) < 0\)
-
C.
\(45.\left( { - 11} \right) < - 500\)
-
D.
\(46.\left( { - 11} \right) < - 500\)
Tính giá trị của lũy thừa \({2^6},\) ta được
-
A.
\(32\)
-
B.
\(64\)
-
C.
\(16\)
-
D.
\(128\)
Tính \(\left( { - 909} \right) + 909.\)
-
A.
$1818$
-
B.
$1$
-
C.
$0$
-
D.
$ - 1818$
Số tự nhiên nhỏ nhất là số
-
A.
\(1\)
-
B.
\(0\)
-
C.
\(2\)
-
D.
\(3\)
\(5125 + 456875\) bằng
-
A.
\(46200\)
-
B.
\(462000\)
-
C.
\(46300\)
-
D.
\(426000\)
Kết quả của phép tính \(23 - 17\) là
-
A.
$ - 40$
-
B.
$ - 6$
-
C.
$40$
-
D.
$6$
-
A.
EF
-
B.
HG
-
C.
HF
-
D.
FG
-
A.
Hình 1, hình 2, hình 4
-
B.
Hình 2, hình 3, hình 4
-
C.
Hình 1, hình 4, hình 5
-
D.
Hình 1, hình 2, hình 5
Kết quả của phép tính $12.100 + 100.36 - 100.19$ là
-
A.
\(29000\)
-
B.
\(3800\)
-
C.
\(290\)
-
D.
\(2900\)
Tìm ƯCLN của $15,45$ và $225$.
-
A.
$18$
-
B.
$3$
-
C.
$15$
-
D.
$5$
Hình chữ nhật có bao nhiêu trục đối xứng
-
A.
1
-
B.
2
-
C.
3
-
D.
4

-
A.
\( - 3\) và \( - 5\)
-
B.
\( - 3\) và \( - 2\)
-
C.
\(1\) và \(2\)
-
D.
\( - 5\) và \( - 6\)
-
A.
Phép cộng của 1 và 2
-
B.
Phép trừ của 2 và 1
-
C.
Phép cộng của 1 và 3
-
D.
Phép trừ của 3 và 1
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là 0
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung
Thứ tự thực hiện phép tính nào sau đây là đúng đối với biểu thức có dấu ngoặc?
-
A.
\(\left[ {} \right] \to \left( {} \right) \to \left\{ {} \right\}\)
-
B.
\(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
-
C.
\(\left\{ {} \right\} \to \left[ {} \right] \to \left( {} \right)\)
-
D.
\(\left[ {} \right] \to \left\{ {} \right\} \to \left( {} \right)\)
Theo dõi kết quả bán hàng trong một ngày của một cửa hàng , người ta nhận thấy:
+) Số tiền thu được vào buổi sáng nhiều hơn vào buổi chiều
+) Số tiền thu được vào buổi tối ít hơn vào buổi chiều.
So sánh số tiền thu được (đều là các số tự nhiên) của cửa hàng vào buổi sáng và buổi tối.
-
A.
Số tiền thu được vào buổi tối ít hơn vào buổi sáng.
-
B.
Số tiền thu được vào buổi tối bằng vào buổi sáng
-
C.
Số tiền thu được vào buổi tối nhiều hơn vào buổi sáng
-
D.
Không so sánh được
Khẳng định nào sau đây sai ?
-
A.
\(a + b + c = \left( {a + b} \right) + c\)
-
B.
\(a + b + c = \left( {a + c} \right) + b\)
-
C.
\(a + b + c = \left( {a + b} \right) + b\)
-
D.
\(a + b + c = a + \left( {b + c} \right)\)
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Có bao nhiêu số tự nhiên \(n\) để \( (n + 4) \, \vdots \, n\) ?
-
A.
\(3\)
-
B.
\(4\)
-
C.
\(2\)
-
D.
\(1\)
Tìm các chữ số $x, y$ biết rằng: \(\overline {23x5y} \) chia hết cho $2; 5$ và $9.$
-
A.
\(x = 0;y = 6\)
-
B.
\(x = 6;y = 0\)
-
C.
\(x = 8;y = 0\)
-
D.
\(x = 0;y = 8\)
Số cách số \( - 2\) sáu đơn vị theo chiều dương là?
-
A.
$6$
-
B.
$ - 8$
-
C.
$4$
-
D.
$5$
Biết \( - 9 < x < 0\). Tập hợp các số nguyên $x$ thỏa mãn:
-
A.
\(A = \left\{ { - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1} \right\}\)
-
B.
\(A = \left\{ { - 9; - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1} \right\}\)
-
C.
\(A = \left\{ { - 9; - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1;0} \right\}\)
-
D.
\(A = \left\{ { - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1;0} \right\}\)
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
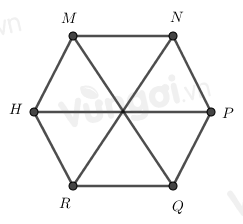
-
A.
8
-
B.
2
-
C.
4
-
D.
6
Cho hình bình hành có chu vi là 480cm, có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
-
A.
5000 cm
-
B.
10000 cm
-
C.
2500 cm 2
-
D.
5000 cm 2

Điền số thích hợp vào ô trống:
\(161291 + \)
\(= (6000 + 725) + 161291\)
Người ta mở rộng một cái ao hình vuông để được một cái ao hình chữ nhật có chiều dài gấp 2 lần chiều rộng. Sau khi mở rộng, diện tích ao tăng thêm 600m 2 và diện tích ao mới gấp 4 lần ao cũ. Hỏi phải dùng bao nhiêu chiếc cọc để đủ rào xung quanh ao mới? Biết rằng cọc nọ cách cọc kia 1m và ở một góc ao người ta để lối lên xuống rộng 3m.
-
A.
120
-
B.
117
-
C.
119
-
D.
122
Cần bao nhiêu chữ số để đánh số trang (bắt đầu từ trang $1$) của một cuốn sách có $1031$ trang?
-
A.
$2017$
-
B.
$3071$
-
C.
$3017$
-
D.
$3008$
Lời giải và đáp án
\(a+b\) bằng?
-
A.
\(a+a\)
-
B.
\(b+b\)
-
C.
\(b+a\)
-
D.
\(a\)
Đáp án : C
Tính chất phép cộng số tự nhiên:
+) Tính chất giao hoán: \(a+b=b+a\) với \(a,b\) là các số tự nhiên.
Có bao nhiêu ước của \( - 24.\)
-
A.
$9$
-
B.
$17$
-
C.
$8$
-
D.
$16$
Đáp án : D
Để tìm tất cả các ước của một số nguyên âm ta chỉ cần tìm tất cả các ước của số đối của số nguyên âm đó. Trước tiên ta tìm ước tự nhiên rồi thêm các ước đối của chúng.
Có \(8\) ước tự nhiên của \(24\) là: \(1;2;3;4;6;8;12;24\)
Có \(8\) ước nguyên âm của \(24\) là: \(-1;-2;-3;-4;-6;-8;-12;-24\)
Vậy có \(8.2 = 16\) ước của \( 24\) nên cũng có $16$ ước của $-24.$
Với ba chữ số \(0;1;3\) có thể viết được bao nhiêu số có ba chữ số khác nhau?
-
A.
\(4\)
-
B.
\(3\)
-
C.
\(5\)
-
D.
\(6\)
Đáp án : A
- Ta viết các số tự nhiên có ba chữ số khác nhau lập thành từ ba số \(0;1;3\) sao cho chữ số hằng trăm khác \(0\).
- Đếm các số.
Có bốn số tự nhiên thỏa mãn đề bài là \(310;301;103;130.\)
Tổng \((a+b)+c\) hay \(a+(b+c)\) được gọi là tổng của ... và viết gọn là \(a+b+c\).
-
A.
kết hợp
-
B.
ba số \(a,b,c\)
-
C.
hai số \(a,b\)
-
D.
giao hoán
Đáp án : B
Tổng \((a+b)+c\) hay \(a+(b+c)\) được gọi là tổng của ba số \(a,b,c\) và viết gọn là \(a+b+c\).
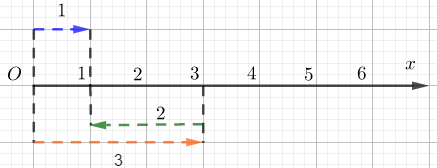
-
A.
Phép cộng của 1 và 2
-
B.
Phép trừ của 3 và 2
-
C.
Phép cộng của 1 và 3
-
D.
Phép trừ của 3 và 1
Đáp án : B
Số 3 và số 1 cùng chiều từ trái sang phải, số 2 ngược chiều với hai số này. Mà ta có 3-2=1 nên hình ảnh trên minh họa cho phép trừ 3-2.
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
Đáp án : A
Sử dụng dấu hiệu nhận biết hình chữ nhật
Hình chữ nhật có bốn đỉnh, hai cặp cạnh đối song song, hai đường chéo bằng nhau.
=> Đáp án B, C, D đúng.
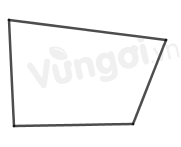
Hình có 4 đỉnh chưa chắc là hình chữ nhật ví dụ:
Viết số 24 bằng số La Mã
-
A.
XXIIII
-
B.
XXIX
-
C.
XXIV
-
D.
XIV
Đáp án : C
- Số từ 21 đến 30 ta viết chữ XX trước.
- Nếu hàng đơn vị là các số từ 1 đến 9 thì ghép chữ số La Mã tương ứng với nó như trong bảng vào.

Chữ số 4 là IV
Ta thêm XX vào bên trái số IV thì được số 24: XXIV
Tập hợp số tự nhiên được kí hiệu là
-
A.
\(N\)
-
B.
\({N^*}\)
-
C.
\(\left\{ N \right\}\)
-
D.
\(Z\)
Đáp án : A
Tập hợp số tự nhiên kí hiệu là N.
Số nào trong các số sau không là số nguyên tố?
-
A.
2
-
B.
3
-
C.
5
-
D.
9
Đáp án : D
- Tìm các ước của 2;3;5;9.
- Số nguyên tố là số tự nhiên lớn hơn \(1,\) chỉ có \(2\) ước là \(1\) và chính nó.
- Chọn số có nhiều hơn 2 ước.
9 chia hết cho 3 nên 3 là một ước của 9. Mà 3 khác 1 và khác 9 nên 9 không là số nguyên tố.
Vậy 9 là số cần tìm.

Viết số chẵn thích hợp vào chỗ trống:
\(550;\,552;\,554;\)
\(;\)
\(;560.\)
\(550;\,552;\,554;\)
\(;\)
\(;560.\)
Xác định quy luật của dãy số trên và tìm số còn thiếu điền vào ô trống.
\(\begin{array}{l}550 + 2 = 552\\552 + 2 = 554\end{array}\)
Suy ra quy luật là: Từ số hạng thứ hai trở đi bằng số hạng liền trước cộng thêm \(2\) đơn vị.
Số thứ tư là: \(554 + 2 = 556\) .
Số thứ năm là: \(556 + 2 = 558\)
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là \(556\,;\,\,558\).
+) Tích của một số chẵn các số nguyên âm là một số nguyên ..(1)..
+) Tích của một số lẻ các số nguyên âm là một số nguyên ..(2)..
Từ thích hợp để điền vào hai chỗ chấm trên lần lượt là:
-
A.
âm, dương
-
B.
dương, âm
-
C.
âm, âm
-
D.
dương, dương
Đáp án : B
- Tích của hai số nguyên trái dấu là số nguyên âm.
- Tính của hai số nguyên cùng dấu là số nguyên dương.
+) Tích của một số chẵn các số nguyên âm là một số nguyên dương
+) Tích của một số lẻ các số nguyên âm là một số nguyên âm
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là $0$ .
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung.
Đáp án : A
- Áp dụng kiến thức:
Mọi số tự nhiên đều có ước là $1$.
Số nguyên tố có $2$ ước là $1$ và chính nó.
Mọi số nguyên tố khác nhau đều có ước chung duy nhất là $1$.
A. Đáp án này đúng vì mọi số tự nhiên đều có ước chung là $1$.
B. Đáp án này sai, vì $0$ không là ước của $1$ số nào cả.
C. Đáp án này sai, vì số nguyên tố có $2$ ước là $1$ và chính nó.
D. Đáp án này sai, vì $2$ số nguyên tố có ước chung là $1$.
BCNN(10, 15, 30) là:
-
A.
10
-
B.
15
-
C.
30
-
D.
60
Đáp án : C
Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho chính là số lớn nhất ấy.
Ta có: 30 là bội của 10 và 15
=> BCNN(10, 15, 30) = 30.
Chọn câu sai.
-
A.
\(\left( { - 19} \right).\left( { - 7} \right) > 0\)
-
B.
\(3.\left( { - 121} \right) < 0\)
-
C.
\(45.\left( { - 11} \right) < - 500\)
-
D.
\(46.\left( { - 11} \right) < - 500\)
Đáp án : C
- Tính và kiểm tra các đáp án, sử dụng quy tắc nhân hai số nguyên cùng dấu, khác dấu.
Đáp án A: \(\left( { - 19} \right).\left( { - 7} \right) > 0\) đúng vì tích hai số nguyên cùng dấu là một số nguyên dương.
Đáp án B: \(3.\left( { - 121} \right) < 0\) đúng vì tích hai số nguyên khác dấu là một số nguyên âm.
Đáp án C: \(45.\left( { - 11} \right) = - 495 > - 500\) nên C sai.
Đáp án D: \(46.\left( { - 11} \right) = - 506 < - 500\) nên D đúng.
Tính giá trị của lũy thừa \({2^6},\) ta được
-
A.
\(32\)
-
B.
\(64\)
-
C.
\(16\)
-
D.
\(128\)
Đáp án : B
Sử dụng công thức \({a^n} = a.a.a...a\) (\(n\) thừa số $a$) để tính giá trị.
Ta có \({2^6} = 2.2.2.2.2.2 = 4.4.4 = 16.4 = 64.\)
Tính \(\left( { - 909} \right) + 909.\)
-
A.
$1818$
-
B.
$1$
-
C.
$0$
-
D.
$ - 1818$
Đáp án : C
Hai số đối nhau có tổng bằng \(0.\)
Ta thấy \(909\) và \(\left( { - 909} \right)\) là hai số đối nhau.
Ta có \(\left( { - 909} \right) + 909 = 0.\)
Số tự nhiên nhỏ nhất là số
-
A.
\(1\)
-
B.
\(0\)
-
C.
\(2\)
-
D.
\(3\)
Đáp án : B
Tập hợp số tự nhiên \(N = \left\{ {0;1;2;3;...} \right\}\)
Nên số tự nhiên nhỏ nhất là số \(0.\)
\(5125 + 456875\) bằng
-
A.
\(46200\)
-
B.
\(462000\)
-
C.
\(46300\)
-
D.
\(426000\)
Đáp án : B
Đặt tính rồi tính.

Vậy \(5125 + 456875 = 462000\)
Kết quả của phép tính \(23 - 17\) là
-
A.
$ - 40$
-
B.
$ - 6$
-
C.
$40$
-
D.
$6$
Đáp án : D
Muốn trừ số nguyên $a$ cho số nguyên $b,$ ta cộng $a$ với số đối của $b:$ $a - b = a + \left( { - b} \right)$
\(23 - 17 = 23 + \left( { - 17} \right) = 6\)
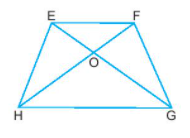
-
A.
EF
-
B.
HG
-
C.
HF
-
D.
FG
Đáp án : D
Sử dụng: Trong hình thang cân hai cạnh bên bằng nhau.
Do góc EH và FG là cạnh bên của hình thang EFGH nên:
\(EH=FG\)
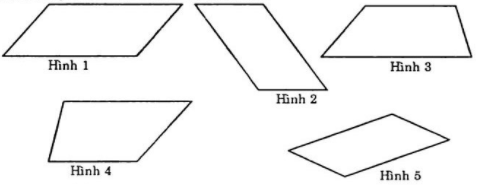
-
A.
Hình 1, hình 2, hình 4
-
B.
Hình 2, hình 3, hình 4
-
C.
Hình 1, hình 4, hình 5
-
D.
Hình 1, hình 2, hình 5
Đáp án : D
Hình bình hành là tứ giác có hai cặp cạnh đối diện song song và bằng nhau.
Các hình là hình bình hành là: Hình 1, hình 2, hình 5
Kết quả của phép tính $12.100 + 100.36 - 100.19$ là
-
A.
\(29000\)
-
B.
\(3800\)
-
C.
\(290\)
-
D.
\(2900\)
Đáp án : D
Sử dụng tính chất phân phối của phép nhân với phép cộng; phép trừ \(ab + ac - ad = a\left( {b + d - c} \right).\)
Ta có $12.100 + 100.36 - 100.19$\( = 100.\left( {12 + 36 - 19} \right) = 100.29 = 2900.\)
Tìm ƯCLN của $15,45$ và $225$.
-
A.
$18$
-
B.
$3$
-
C.
$15$
-
D.
$5$
Đáp án : C
- Phân tích mỗi số ra thừa số nguyên tố.
- Tìm thừa số nguyên tố chung.
- Lập tích của các số tìm được với số mũ nhỏ nhất.
Tích đó chính là ước chung lớn nhất.
Ta có: \(15 = 3.5;\) \(45 = {3^2}.5;\) \(225 = {5^2}{.3^2}\)
Nên ƯCLN\(\left( {15;45;225} \right) = 3.5 = 15.\)
Hình chữ nhật có bao nhiêu trục đối xứng
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Đáp án : B
Trục đối xứng của hình chữ nhật là đường thẳng đi qua trung điểm hai đáy.

Vậy hình chữ nhật có 2 trục đối xứng.

-
A.
\( - 3\) và \( - 5\)
-
B.
\( - 3\) và \( - 2\)
-
C.
\(1\) và \(2\)
-
D.
\( - 5\) và \( - 6\)
Đáp án : B
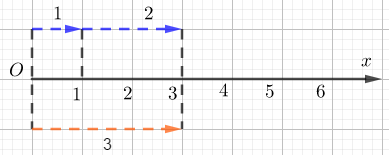
-
A.
Phép cộng của 1 và 2
-
B.
Phép trừ của 2 và 1
-
C.
Phép cộng của 1 và 3
-
D.
Phép trừ của 3 và 1
Đáp án : A
Số 1, 2 và 3 đều có chiều từ trái sang phải. Mà 1+2=3 nên đây là hình ảnh minh họa cho phép cộng 1 và 2.
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là 0
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung
Đáp án : A
- Áp dụng kiến thức:
Mọi số tự nhiên đều có ước là $1$.
Số nguyên tố có $2$ ước là $1$ và chính nó.
Mọi số nguyên tố khác nhau đều có ước chung duy nhất là $1$.
A. Đáp án này đúng vì mọi số tự nhiên đều có ước chung là $1$
B. Đáp án này sai, vì $0$ không là ước của $1$ số nào cả.
C. Đáp án này sai, vì số nguyên tố có $2$ ước là $1$ và chính nó.
D. Đáp án này sai, vì $2$ số nguyên tố có ước chung là $1$.
Thứ tự thực hiện phép tính nào sau đây là đúng đối với biểu thức có dấu ngoặc?
-
A.
\(\left[ {} \right] \to \left( {} \right) \to \left\{ {} \right\}\)
-
B.
\(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
-
C.
\(\left\{ {} \right\} \to \left[ {} \right] \to \left( {} \right)\)
-
D.
\(\left[ {} \right] \to \left\{ {} \right\} \to \left( {} \right)\)
Đáp án : B
Nếu biểu thức có các dấu ngoặc : ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính theo thứ tự : \(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}\)
Theo dõi kết quả bán hàng trong một ngày của một cửa hàng , người ta nhận thấy:
+) Số tiền thu được vào buổi sáng nhiều hơn vào buổi chiều
+) Số tiền thu được vào buổi tối ít hơn vào buổi chiều.
So sánh số tiền thu được (đều là các số tự nhiên) của cửa hàng vào buổi sáng và buổi tối.
-
A.
Số tiền thu được vào buổi tối ít hơn vào buổi sáng.
-
B.
Số tiền thu được vào buổi tối bằng vào buổi sáng
-
C.
Số tiền thu được vào buổi tối nhiều hơn vào buổi sáng
-
D.
Không so sánh được
Đáp án : A
Sử dụng tính chất bắc cầu: so sánh buổi sáng với chiều, chiều với tối.
Số tiền buổi sáng nhiều hơn buổi chiều.
Mà số tiền thu được vào buổi chiều nhiều hơn vào buổi tối vì số tiền thu được vào buổi tối ít hơn vào buổi chiều.
Do đó số tiền buổi sáng nhiều hơn số tiền thu được buổi tối.
Vậy số tiền thu được buổi tối ít hơn số tiền thu được buổi sáng.
Khẳng định nào sau đây sai ?
-
A.
\(a + b + c = \left( {a + b} \right) + c\)
-
B.
\(a + b + c = \left( {a + c} \right) + b\)
-
C.
\(a + b + c = \left( {a + b} \right) + b\)
-
D.
\(a + b + c = a + \left( {b + c} \right)\)
Đáp án : C
- Áp dụng tính chất giao hoán của phép cộng.
- Áp dụng tính chất kết hợp của phép cộng.
\(a + b + c = \left( {a + b} \right) + b\) sai vì \(c\) không thể bằng \(b\).
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Đáp án : B
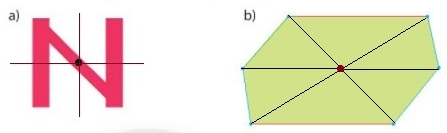
=> Hình a và hình b là hình có tâm đối xứng.
Vậy có 2 hình có tâm đối xứng.
Có bao nhiêu số tự nhiên \(n\) để \( (n + 4) \, \vdots \, n\) ?
-
A.
\(3\)
-
B.
\(4\)
-
C.
\(2\)
-
D.
\(1\)
Đáp án : A
Sử dụng tính chất 1: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó để suy ra điều kiện của \(n.\)
Vì \(n \, \vdots \, n\) nên để \((n + 4) \, \vdots \, n\) thì \(4 \, \vdots \, n\) suy ra \(n \in \left\{ {1;2;4} \right\}\)
Vậy có ba giá trị của \(n\) thỏa mãn điều kiện đề bài.
Tìm các chữ số $x, y$ biết rằng: \(\overline {23x5y} \) chia hết cho $2; 5$ và $9.$
-
A.
\(x = 0;y = 6\)
-
B.
\(x = 6;y = 0\)
-
C.
\(x = 8;y = 0\)
-
D.
\(x = 0;y = 8\)
Đáp án : C
Điều kiện: \(x; y \in \left\{ {0;\,\,1;\,\,2;\,\,.......;\,\,9} \right\}\)
Vì \(\overline {23x5y} \) chia hết cho cả $2$ và $5$ nên \(y = 0\) ta được số \(\overline {23x50} \) .
Số \(\overline {23x50} \,\, \vdots \,\,9 \Rightarrow \left( {2 + 3 + x + 5 + 0} \right)\,\, \vdots \,\,9 \Rightarrow \left( {10 + x} \right)\,\, \vdots \,\,9 \Rightarrow x = 8.\)
Vậy \(x = 8;y = 0\), ta có số $23850.$
Số cách số \( - 2\) sáu đơn vị theo chiều dương là?
-
A.
$6$
-
B.
$ - 8$
-
C.
$4$
-
D.
$5$
Đáp án : C
Điểm nằm cách điểm A theo chiều dương tức là điểm đó nằm bên tay phải điểm A Điểm nằm cách điểm A theo chiều âm tức là điểm đó nằm bên trái điểm A

Ta đếm về bên phải số $ - 2$ sáu đơn vị được số $4$ ( hay $ + 4$ ) Vậy số cách số $ - 2$ sáu đơn vị theo chiều dương là: $4$ ( hay $ + 4$)
Biết \( - 9 < x < 0\). Tập hợp các số nguyên $x$ thỏa mãn:
-
A.
\(A = \left\{ { - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1} \right\}\)
-
B.
\(A = \left\{ { - 9; - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1} \right\}\)
-
C.
\(A = \left\{ { - 9; - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1;0} \right\}\)
-
D.
\(A = \left\{ { - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1;0} \right\}\)
Đáp án : A
Vì $x$ là số nguyên nên dựa vào điều kiện đề bài ta tìm được giá trị của $x$ và viết chúng dưới dạng tập hợp.
Vì \( - 9 < x < 0;x \in Z \Rightarrow x \in \left\{ { - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1} \right\}\)
Do đó \(A = \left\{ { - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1} \right\}\).
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều

-
A.
8
-
B.
2
-
C.
4
-
D.
6
Đáp án : D
Đếm số tam giác đều đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
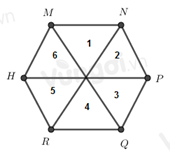
Ta đánh số như hình trên
Nhận thấy có các hình tam giác đều là: 1, 2, 3, 4, 5, 6.
Vậy có 6 tam giác đều.
Cho hình bình hành có chu vi là 480cm, có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
-
A.
5000 cm
-
B.
10000 cm
-
C.
2500 cm 2
-
D.
5000 cm 2
Đáp án : D
- Tính nửa chu vi hình bình hành
- Tính cạnh đáy của hình bình hành
- Tính chiều cao của hình bình hành
=> Diện tích hình bình hành
Diện tích hình bình hành là: \(S = b.h\)
Trong đó \(b\) là cạnh, \(h\) là chiều cao tương ứng.
- Ta có nửa chu vi hình bình hành là: 480 : 2 = 240 (cm)
Cạnh đáy gấp 5 lần cạnh kia nên nửa chu vi sẽ gấp 6 lần cạnh kia.
- Ta có cạnh đáy hình bình hành là: 240 : 6 . 5 = 200 (cm)
- Chiều cao của hình bình hành là: 200 : 8 = 25 (cm)
- Diện tích của hình bình hành là: 200 . 25 = 5000 (cm 2 )

Điền số thích hợp vào ô trống:
\(161291 + \)
\(= (6000 + 725) + 161291\)
\(161291 + \)
\(= (6000 + 725) + 161291\)
Áp dụng tính chất giao hoán của phép cộng: Khi đổi chỗ các số hạng trong một tổng thì tổng đó không thay đổi.
Ta có: \((6000 + 725) + 161291 = 6725 + 161291\)
Hay \(161291 + 6725 = (6000 + 725) + 161291\)
Vậy đáp án đúng điền vào ô trống là \(6725\).
Người ta mở rộng một cái ao hình vuông để được một cái ao hình chữ nhật có chiều dài gấp 2 lần chiều rộng. Sau khi mở rộng, diện tích ao tăng thêm 600m 2 và diện tích ao mới gấp 4 lần ao cũ. Hỏi phải dùng bao nhiêu chiếc cọc để đủ rào xung quanh ao mới? Biết rằng cọc nọ cách cọc kia 1m và ở một góc ao người ta để lối lên xuống rộng 3m.
-
A.
120
-
B.
117
-
C.
119
-
D.
122
Đáp án : B
- Tính diện tích áo mới.
- Tính diện tích hình vuông khi chia ao mới thành hai hình vuông có diện tích bằng nhau.
=> Chiều dài và chiều rộng của ao mới.
- Tính chu vi áo mới.
- Tính số cọc để rào xung quanh ao mới.
Ta có sơ đồ:
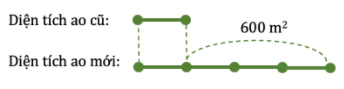
Diện tích ao mới là:
600 : (4 – 1) . 4 = 800 (m 2 )
Ta chia ao mới thành hai hình vuông có diện tích bằng nhau như hình vẽ. Diện tích một hình vuông là:
800 : 2 = 400 (m 2 )
Vì 400 = 20 . 20
Cạnh của hình vuông hay chiều rộng của ao mới là 20m
Chiều dài của ao mới là: 20 . 2 = 40 (m)
Chu vi áo mới là:
(40 + 20) . 2 = 120(m)
Số cọc để rào xung quanh ao mới là:
(120 – 3) : 1 = 117 (chiếc)
Cần bao nhiêu chữ số để đánh số trang (bắt đầu từ trang $1$) của một cuốn sách có $1031$ trang?
-
A.
$2017$
-
B.
$3071$
-
C.
$3017$
-
D.
$3008$
Đáp án : C
Chia số trang thành các nhóm để dễ dàng tính được số chữ số cần dùng trong mỗi nhóm, từ đó tính được tổng số chữ số cần dùng.
Ta chia các số trang của cuốn sách thành 4 nhóm:
+ Nhóm các số có $1$ chữ số (từ trang $1$ đến trang $9$): số chữ số cần dùng là $9$.
+ Nhóm các số có hai chữ số (từ trang $10$ đến trang $99$): số trang sách là: \(\left( {99 - 10} \right):1 + 1 = 90\), số chữ số cần dùng là: \(90.2 = 180\) .
+ Nhóm các số có $3$ chữ số (từ trang $100$ đến trang $999$): số trang sách là: \(\left( {999 - 100} \right):1 + 1 = 900\), số chữ số cần dùng để đánh số trang nhóm này là: \(900.3 = 2700\).
+Nhóm các số có $4$ chữ số (từ trang $1000$ đến trang $1031$): số trang sách là: \(\left( {1031 - 1000} \right):1 + 1 = 32\) ; số chữ số cần dùng là \(32.4 = 128\) .
Vậy tổng số chữ số cần dùng để đánh số trang cuốn sách đó là: \(9 + 180 + 2700 + 128 = 3017\)