Đề kiểm tra 15 phút Toán 6 Kết nối tri thức - Đề số 5
Đề bài
Chọn phát biểu sai :
-
A.
Tam giác đều có ba cạnh
-
B.
Ba cạnh của tam giác đều bằng nhau
-
C.
Bốn góc của tam giác đều bằng nhau
-
D.
Tam giác đều có ba đỉnh
Đoạn thẳng AB có độ dài 4 cm. Gọi O là tâm đối xứng của đoạn thẳng AB. Tính độ dài đoạn OA.
-
A.
2 cm
-
B.
4 cm
-
C.
6 cm
-
D.
8 cm
-
A.
Chiếc bàn có tâm đối xứng
-
B.
Chiếc bàn có trục đối xứng
-
C.
Chiếc bàn vừa có tâm đối xứng và trục đối xứng
-
D.
Chiếc bàn không có tâm đối xứng và trục đối xứng
Cho các hình sau đây:
(1) Đoạn thẳng AB
(2) Tam giác đều ABC
(3) Hình tròn tâm O
Trong các hình nói trên, các hình có tâm đối xứng là
-
A.
(1)
-
B.
(1), (2)
-
C.
(1), (3)
-
D.
(1), (2), (3)
-
A.
Góc E
-
B.
Góc F
-
C.
Góc G
-
D.
Góc O
Cho diện tích tứ giác (1) bằng \(20\,\,c{m^2}\), Diện tích tam giác (2) bằng \(16\,\,c{m^2}\), Khi đó diện tích của hình trên bằng:
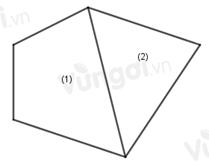
-
A.
\(36\,cm\)
-
B.
\(36\,d{m^2}\)
-
C.
\(26\,c{m^2}\)
-
D.
\(36\,\,c{m^2}\)
-
A.
Hình a) và c) có trục đối xứng
-
B.
Hình c) có trục đối xứng
-
C.
Hình b) và c) có trục đối xứng
-
D.
Cả 3 hình có trục đối xứng
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
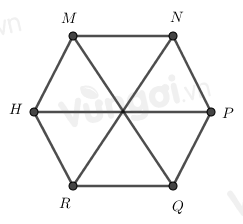
-
A.
8
-
B.
2
-
C.
4
-
D.
6

Độ dài đáy của hình bình hành có chiều cao \(24cm\) và diện tích là \(432c{m^2}\) là:
A. \(16cm\)
B. \(17cm\)
C. \(18cm\)
D. \(19cm\)
-
A.
9
-
B.
14
-
C.
10
-
D.
13
Lời giải và đáp án
Chọn phát biểu sai :
-
A.
Tam giác đều có ba cạnh
-
B.
Ba cạnh của tam giác đều bằng nhau
-
C.
Bốn góc của tam giác đều bằng nhau
-
D.
Tam giác đều có ba đỉnh
Đáp án : C
Trong tam giác đều ba góc bằng nhau => Đáp án C sai.
Đoạn thẳng AB có độ dài 4 cm. Gọi O là tâm đối xứng của đoạn thẳng AB. Tính độ dài đoạn OA.
-
A.
2 cm
-
B.
4 cm
-
C.
6 cm
-
D.
8 cm
Đáp án : A
Tâm đối xứng của một đoạn thẳng chia đôi đoạn thẳng đó thành hai phần bằng nhau
Độ dài đoạn OA là: \(4:2 = 2\left( {cm} \right)\)
-
A.
Chiếc bàn có tâm đối xứng
-
B.
Chiếc bàn có trục đối xứng
-
C.
Chiếc bàn vừa có tâm đối xứng và trục đối xứng
-
D.
Chiếc bàn không có tâm đối xứng và trục đối xứng
Đáp án : C
Quan sát hình vẽ ta thấy: Chiếc đĩa vừa có tâm đối xứng và trục đối xứng
Cho các hình sau đây:
(1) Đoạn thẳng AB
(2) Tam giác đều ABC
(3) Hình tròn tâm O
Trong các hình nói trên, các hình có tâm đối xứng là
-
A.
(1)
-
B.
(1), (2)
-
C.
(1), (3)
-
D.
(1), (2), (3)
Đáp án : C
- Tâm đối xứng của đoạn thẳng AB là trung điểm của đoạn thẳng AB.
- Tam giác đều ABC không có tâm đối xứng
- Tâm đối xứng của đường tròn tâm O là điểm O.
Vậy (1) và (3) là hình có tâm đối xứng
-
A.
Góc E
-
B.
Góc F
-
C.
Góc G
-
D.
Góc O
Đáp án : C
Sử dụng: Hai góc kề một cạnh bên của hình thang cân bằng nhau.
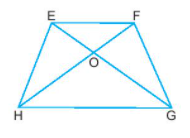
Do góc H và góc G cùng kề đáy HG của hình thang EFGH nên:
Góc H bằng góc G.
Cho diện tích tứ giác (1) bằng \(20\,\,c{m^2}\), Diện tích tam giác (2) bằng \(16\,\,c{m^2}\), Khi đó diện tích của hình trên bằng:

-
A.
\(36\,cm\)
-
B.
\(36\,d{m^2}\)
-
C.
\(26\,c{m^2}\)
-
D.
\(36\,\,c{m^2}\)
Đáp án : D
Diện tích hình đã cho bằng tổng diện tích tứ giác (1) và (2).
Diện tích hình đã cho là: \(20 + 16 = 36\) (\(c{m^2}\)).
-
A.
Hình a) và c) có trục đối xứng
-
B.
Hình c) có trục đối xứng
-
C.
Hình b) và c) có trục đối xứng
-
D.
Cả 3 hình có trục đối xứng
Đáp án : B

Ta có chữ N và Z không có trục đối xứng, chữ O có trục đối xứng.
Vậy hình c) có trục đối xứng.
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều

-
A.
8
-
B.
2
-
C.
4
-
D.
6
Đáp án : D
Đếm số tam giác đều đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
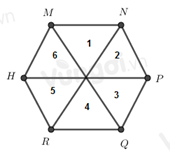
Ta đánh số như hình trên
Nhận thấy có các hình tam giác đều là: 1, 2, 3, 4, 5, 6.
Vậy có 6 tam giác đều.

Độ dài đáy của hình bình hành có chiều cao \(24cm\) và diện tích là \(432c{m^2}\) là:
A. \(16cm\)
B. \(17cm\)
C. \(18cm\)
D. \(19cm\)
C. \(18cm\)
Từ công thức tính diện tích hình bình hành: \(S = a \times h\), ta có thể suy ra công thức tính độ dài cạnh đáy \(a\) là \(a = S:h\).
Độ dài đáy của hình bình hành đó là:
\(432:24 = 18\,\,(cm)\)
Đáp số: \(18cm\).
-
A.
9
-
B.
14
-
C.
10
-
D.
13
Đáp án : B
Đếm số hình vuông nhỏ + số hình vuông được ghép từ các ô vuông nhỏ.
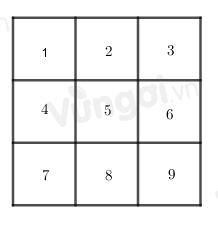
Ta đánh số như hình trên:
+ 9 hình vuông nhỏ là: 1, 2, 3, 4, 5, 6, 7, 8, 9.
+ 4 hình vuông được gép từ bốn hình vuông nhỏ là: 1245, 2356, 4578, 5689.
+ 1 hình vuông lớn được ghép từ 9 hình vuông nhỏ.
Vậy có tất cả \(9 + 4 + 1 = 14\) hình vuông.


