Đề số 21 - Đề kiểm tra học kì 1 - Toán 9 — Không quảng cáo

Đề bài

Câu 1 (2,0 điểm):

Cho biểu thức: \(P = \left( {\dfrac{{2\sqrt x  + 1}}{{x + \sqrt x }} - \dfrac{{1 - \sqrt x }}{{\sqrt x }}} \right):\left( {1 + \dfrac{2}{{\sqrt x }}} \right)\) với \(x > 0\).

1. Rút gọn P .

2. Tính giá trị của P biết \(x = 2019 - 2\sqrt {2018} \)

Câu 2 (2,5 điểm):

Cho hàm số \(y = \left( {{m^2} - 2m + 3} \right)x - 4\,\,\,\,\,\left( d \right)\), (với m là tham số)

1. Chứng minh rằng với mọi m hàm số luôn đồng biến trên tập xác định của nó.

2. Tìm m để \(\left( d \right)\) đi qua \(A\left( {2;8} \right)\).

3. Tìm m để \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right):y = 3x + m - 4\).

Câu 3 (2,0 điểm):

Cho hệ phương trình \(\left\{ \begin{array}{l}mx + y = {x^2} + 3\\x - y =  - 4\end{array} \right.\)  (với m là tham số)

1. Giải hệ với \(m = 3\).

2. Chứng minh rằng với mọi \(m \ne  - 1\) hệ phương trình có nghiệm duy nhất \(\left( {x,y} \right)\). Khi đó tìm giá trị nhỏ nhất của biểu thức \(Q = {x^2} - 2y + 10\).

Câu 4 (3,0 điểm) : Cho đường tròn tâm O , bán kính R và đường thẳng \(\left( \Delta  \right)\) không có điểm chung với đường tròn \(\left( O \right)\), H là hình chiếu vuông góc của O trên \(\left( \Delta  \right)\). Từ điểm M bất kỳ trên \(\left( \Delta  \right)\) (\(M \ne H\)), vẽ hai tiếp tuyến MA, MB tới đường tròn \(\left( O \right)\) ( A, B là hai tiếp điểm). Gọi K, I thứ tự là giao điểm của AB với OM và OH .

1. Chứng minh \(AB = 2AK\) và 5 điểm M, A, O, B, H cùng thuộc một đường tròn.

2. Chứng minh \(OI.OH = OK.OM = {R^2}\).

3. Trên đoạn OA lấy điểm N sao cho \(AN = 2ON\). Đường trung trực của BN cắt OM ở E . Tính tỉ số \(\dfrac{{OE}}{{OM}}\).

Câu 5 (0,5 điểm) :

Giải phương trình: \(\sqrt {x + y - 4}  + \sqrt {x - y + 4}  + \sqrt { - x + y + 4}  = \sqrt x  + \sqrt y  + 2\)

Lời giải chi tiết

Câu 1:

Cho biểu thức: \(P = \left( {\dfrac{{2\sqrt x  + 1}}{{x + \sqrt x }} - \dfrac{{1 - \sqrt x }}{{\sqrt x }}} \right):\left( {1 + \dfrac{2}{{\sqrt x }}} \right)\) với \(x > 0\).

1. Rút gọn P .

\(\begin{array}{l}P = \left( {\dfrac{{2\sqrt x  + 1}}{{x + \sqrt x }} - \dfrac{{1 - \sqrt x }}{{\sqrt x }}} \right):\left( {1 + \dfrac{2}{{\sqrt x }}} \right)\\ = \dfrac{{2\sqrt x  + 1 - \left( {1 - \sqrt x } \right).\left( {\sqrt x  + 1} \right)}}{{\sqrt x .\left( {\sqrt x  + 1} \right)}}:\dfrac{{\sqrt x  + 2}}{{\sqrt x }}\\ = \dfrac{{2\sqrt x  + 1 - 1 + x}}{{\sqrt x .\left( {\sqrt x  + 1} \right)}}.\dfrac{{\sqrt x }}{{\sqrt x  + 2}} \\= \dfrac{{\sqrt x \left( {\sqrt x  + 2} \right)}}{{\sqrt x .\left( {\sqrt x  + 1} \right)}}.\dfrac{{\sqrt x }}{{\sqrt x  + 2}} = \dfrac{{\sqrt x }}{{\sqrt x  + 1}}\end{array}\)

2. Tính giá trị của P biết \(x = 2019 - 2\sqrt {2018} \)

\(x = 2019 - 2\sqrt {2018}  = 2018 - 2\sqrt {2018}  + 1 = {\left( {\sqrt {2018}  - 1} \right)^2}\)

\(\Rightarrow \sqrt x  = \left| {\sqrt {2018}  - 1} \right| = \sqrt {2018}  - 1\)

\( \Rightarrow P = \dfrac{{\sqrt x }}{{\sqrt x  + 1}} = \dfrac{{\sqrt {2018}  - 1}}{{\sqrt {2018}  - 1 + 1}} = \dfrac{{\sqrt {2018}  - 1}}{{\sqrt {2018} }} = 1 - \dfrac{1}{{\sqrt {2018} }}\)

Câu 2:

Cho hàm số \(y = \left( {{m^2} - 2m + 3} \right)x - 4\,\,\,\,\,\left( d \right)\), (với m là tham số)

1. Chứng minh rằng với mọi m hàm số luôn đồng biến trên tập xác định của nó.

\({m^2} - 2m + 3 = {m^2} - 2m + 1 + 2 = {\left( {m - 1} \right)^2} + 2 > 0\) với mọi m

Vậy với mọi m hàm số luôn đồng biến trên tập xác định của nó

2. Tìm m để \(\left( d \right)\) đi qua \(A\left( {2;8} \right)\).

Để \(\left( d \right)\) đi qua \(A\left( {2;8} \right)\) \( \Leftrightarrow \)\(8 = \left( {{m^2} - 2m + 3} \right).2 - 4 \Leftrightarrow 2{m^2} - 4m + 6 - 4 - 8 = 0\)

\( \Leftrightarrow 2{m^2} - 4m - 6 = 0 \)

\(\Leftrightarrow 2{m^2} + 2m - 6m - 6 = 0\)

\(\Leftrightarrow 2m\left( {m + 1} \right) - 6\left( {m + 1} \right) = 0\)

\(\Leftrightarrow \left( {m + 1} \right)\left( {2m - 6} \right) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}m + 1 = 0\\2m - 6 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m =  - 1\\m = 3\end{array} \right.\)

Vậy với \(m =  - 1\) hoặc \(m = 3\) thì \(\left( d \right)\) đi qua \(A\left( {2;8} \right)\)

3. Tìm m để \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right):y = 3x + m - 4\).

Để \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right):y = 3x + m - 4\)

\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 2m + 3 = 3\\ - 4 \ne m - 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 2m = 0\\m \ne 0\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}m\left( {m - 2} \right) = 0\\m \ne 0\end{array} \right. \Leftrightarrow m = 2\)

Vậy với \(m = 2\) thì \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right):y = 3x + m - 4\).

Câu 3:

Cho hệ phương trình \(\left\{ \begin{array}{l}mx + y = {m^2} + 3\\x - y =  - 4\end{array} \right.\)  (với m là tham số)

1. Giải hệ với \(m = 3\).

Với \(m = 3\) hệ phương trình thành:

\(\left\{ \begin{array}{l}3x + y = {3^2} + 3\\x - y =  - 4\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}3x + x + 4 = 12\\y = x + 4\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}4x = 8\\y = x + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 6\end{array} \right.\)

Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {2;6} \right)\)

2. Chứng minh rằng với mọi \(m \ne  - 1\) hệ phương trình có nghiệm duy nhất \(\left( {x,y} \right)\). Khi đó tìm giá trị nhỏ nhất của biểu thức \(Q = {x^2} - 2y + 10\).

Với \(m \ne  - 1\) ta có:

\(\left\{ \begin{array}{l}mx + y = {m^2} + 3\\x - y =  - 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}mx + x + 4 = {m^2} + 3\\y = x + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left( {m + 1} \right)x = {m^2} - 1\\y = x + 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = m - 1\\y = m + 3\end{array} \right.\)

Vậy với mọi \(m \ne  - 1\) hệ phương trình có nghiệm duy nhất \(\left( {x,y} \right) = \left( {m - 1;m + 3} \right)\)

\(Q = {x^2} - 2y + 10 = {x^2} - 2\left( {x + 4} \right) + 10 \)\(\,= {x^2} - 2x + 2 = {\left( {x - 1} \right)^2} + 1 \ge 1\) với mọi x

Dấu ‘=’ xảy ra \( \Leftrightarrow x - 1 = 0 \Leftrightarrow x = 1 \Leftrightarrow m = 2\)

Vậy \({\min _Q} = 1\) đạt được khi \(m = 2\)

Câu 4:

Cho đường tròn tâm O , bán kính R và đường thẳng \(\left( \Delta  \right)\) không có điểm chung với đường tròn \(\left( O \right)\), H là hình chiếu vuông góc của O trên \(\left( \Delta  \right)\). Từ điểm M bất kỳ trên \(\left( \Delta  \right)\) (\(M \ne H\)), vẽ hai tiếp tuyến MA, MB tới đường tròn \(\left( O \right)\) ( A, B là hai tiếp điểm). Gọi K, I thứ tự là giao điểm của AB với OM và OH .

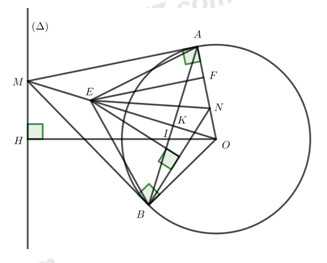
1. Chứng minh \(AB = 2AK\) và 5 điểm M, A, O, B, H cùng thuộc một đường tròn.

Có MA, MB là hai tiếp tuyến của đường tròn \(\left( O \right)\)

\( \Rightarrow \angle AMK = \angle BMK\) và \(MA = MB\) (tính chất hai tiếp tuyến cắt nhau)

Xét \(\Delta AMK\) và \(\Delta BMK\) có: MK chung ; \(\angle AMK = \angle BMK\); \(MA = MB\) (cmt)

\( \Rightarrow \Delta AMK = \Delta BMK\)  (c.g.c) \( \Rightarrow AK = BK\) (2 cạnh tương ứng)

\( \Rightarrow AB = AK + BK = AK + AK = 2AK\)

Ta có: \(\angle OHM = \angle OAM = \angle OBM = {90^o}\) (\(OH \bot \left( \Delta  \right)\) và MA, MB là hai tiếp tuyến của đường tròn \(\left( O \right)\))

\( \Rightarrow \) H, A, B cùng thuộc đường tròn đường kính OM

\( \Rightarrow \) M, A, O, B, H cùng thuộc đường tròn đường kính OM

2. Chứng minh \(OI.OH = OK.OM = {R^2}\).

Có \(\Delta AMK = \Delta BMK\) (cmt) \( \Rightarrow \angle AKM = \angle BKM\) mà \(\angle AKM + \angle BKM = {180^o}\)

\( \Rightarrow \angle AKM = \angle BKM = {90^o} \Rightarrow AB \bot MN \Rightarrow \angle OKI = {90^o}\)

Xét \(\Delta OIK\) và \(\Delta OMH\) có: \(\angle O\) chung ; \(\angle OKI = \angle OHM = {90^o}\)

\(\Delta OIK \sim \Delta OMH\)   (g.g) \( \Rightarrow \dfrac{{OI}}{{OM}} = \dfrac{{OK}}{{OH}} \Rightarrow OI.OH = OK.OM\)

Xét \(\Delta BOM\) vuông tại B đường cao BK ta có: \(OK.OM = O{B^2} = {R^2}\)

\( \Rightarrow \)\(OI.OH = OK.OM = {R^2}\) (đpcm)

3. Trên đoạn OA lấy điểm N sao cho \(AN = 2ON\). Đường trung trực của BN cắt OM ở E . Tính tỉ số \(\dfrac{{OE}}{{OM}}\).

Ta có \(MA = MB\,\,;\,\,OA = OB\) (tính chất hai tiếp tuyến cắt nhau)

\( \Rightarrow \) OM là đường trung trực của AB \( \Rightarrow EA = EB\) (\(E \in OM\))

Mặt khác \(EB = EN\) ( E thuộc đường trung trực của BN ) \( \Rightarrow EA = EN\)

\( \Rightarrow \Delta AEN\) cân tại E

Gọi F là trung điểm của AN thì EF là đường trung tuyến đồng thời là đường cao của \(\Delta AEN\) cân tại E

\( \Rightarrow EF \bot OA\) mà \(OA \bot MA\) (tính chất tiếp tuyến)

\( \Rightarrow EF//MA\) (từ vuông góc đến song song)

Xét \(\Delta OAM\) có \(EF//MA\) nên theo định lý Ta-lét ta có: \(\dfrac{{OE}}{{OM}} = \dfrac{{OF}}{{OA}}\)

Vì \(AN = 2ON\) và F là trung điểm của AN nên \(AF = FN = ON \Rightarrow \dfrac{{OF}}{{OA}} = \dfrac{2}{3} \Rightarrow \dfrac{{OE}}{{OM}} = \dfrac{2}{3}\)

Câu 5:

Giải phương trình: \(\sqrt {x + y - 4}  + \sqrt {x - y + 4}  + \sqrt { - x + y + 4}  = \sqrt x  + \sqrt y  + 2\)

+) Với \(a \ge 0\,\,;\,\,b \ge 0\) ta có:

\({\left( {\sqrt a  - \sqrt b } \right)^2} \ge 0\)

\(\Leftrightarrow a - 2\sqrt {ab}  + b \ge 0 \Leftrightarrow a + b \ge 2\sqrt {ab} \)

\(\Leftrightarrow 2\left( {a + b} \right) \ge {\left( {\sqrt a  + \sqrt b } \right)^2}\)

\( \Leftrightarrow \sqrt a  + \sqrt b  \le \sqrt {2\left( {a + b} \right)} \)   (*)

Dấu ‘=’ xảy ra khi \(a = b\)

+) Điều kiện: \(x\,,y \ge 0\,\,;\,\,x + y - 4 \ge 0\,\,;\,\,x - y + 4 \ge 0\,\,;\,\, - x + y + 4 \ge 0\,\)

Áp dụng bất đẳng thức (*) ta được:

\(\sqrt {x + y - 4}  + \sqrt {x - y + 4}  \le \sqrt {2\left( {x + y - 4 + x - y + 4} \right)}  = 2\sqrt x \)    (1)

\(\sqrt {x + y - 4}  + \sqrt { - x + y + 4}  \le \sqrt {2\left( {x + y - 4 - x + y + 4} \right)}  = 2\sqrt y \)    (2)

\(\sqrt {x - y + 4}  + \sqrt { - x + y + 4}  \le \sqrt {2\left( {x - y + 4 - x + y + 4} \right)}  = 4\)    (3)

Từ (1), (2), (3) suy ra:

\(2\sqrt {x + y - 4}  + 2\sqrt {x - y + 4}  + 2\sqrt { - x + y + 4}  \le 2\sqrt x  + 2\sqrt y  + 4\)

\( \Rightarrow \sqrt {x + y - 4}  + \sqrt {x - y + 4}  + \sqrt { - x + y + 4}  \le \sqrt x  + \sqrt y  + 2\)

Dấu ‘=’ xảy ra khi: \(\left\{ \begin{array}{l}x + y - 4 = x - y + 4\\x + y - 4 =  - x + y + 4\\x - y + 4 =  - x + y + 4\end{array} \right. \Leftrightarrow x = y = 4\) (thỏa mãn điều kiện)

Vậy phương trình có nghiệm là \(x = y = 4\)