Đề số 24 - Đề thi vào lớp 10 môn Toán — Không quảng cáo

Đề bài

Bài 1 (2 điểm):

Cho biểu thức: $A = \left( {\dfrac{1}{{x + \sqrt x }} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{\sqrt x }}{{x + 2\sqrt x  + 1}},$ với $x > 0.$

a) Rút gọn biểu thức: $A.$

b) Tìm các giá trị của $x$ để $A > \dfrac{1}{2}.$

Bài 2 (2,0 điểm):

1) Không dùng máy tính, trình bày cách giải hệ phương trình: $\left\{ \begin{array}{l}2x - y = 4\\x + 3y =  - 5\end{array} \right..$

2) Trong mặt phẳng tọa độ $Oxy$ đường thẳng $d$ có hệ số góc $k$ đi qua điểm $M\left( {1; - 3} \right)$ cắt các trục $Ox,\;\;Oy$ lần lượt tại $A$ và $B.$

a) Xác định tọa độ các điểm $A,\;\;B$ theo $k.$

b) Tính diện tích tam giác $OAB$ khi $k = 2.$

Bài 3 (2,0 điểm). Tìm một số có hai chữ số biết rằng: Hiệu của số ban đầu với số đảo ngược của nó bằng  18 (số đảo ngược của một số là số thu được bằng cách viết các chữ số của số đó theo thứ tự ngược lại) và tổng của số ban đầu với bình phương số đảo ngược của nó bằng 618.

Bài 4 (3,0 điểm)

Cho tam giác đều ABC có đường cao AH. Trên cạnh BC lấy điểm M tùy ý (M không trùng với B, C, H). Gọi P, Q lần lượt là hình chiếu vuông góc vủa M lên AB và AC.

a)  Chứng minh tứ giác APMQ nội tiếp được trong đường tròn và xác định tâm O của đường tròn này.

b)  Chứng minh $OH \bot PQ$.

c)  Chứng minh $MP + MQ = AH$.

Bài 5 (1,0 điểm):

Cho tam giác đều $ABC$ có cạnh bằng $a.$ Hai điểm $M,\;N$ lần lượt di động trên hai đoạn thẳng $AB,\;\;AC$ sao cho $\dfrac{{AM}}{{MB}} + \dfrac{{AN}}{{NC}} = 1.$ Đặt $AM = x$ và $AN = y.$ Chứng minh: $MN = a - x - y.$

Lời giải chi tiết

Bài 1:

Cho biểu thức: $A = \left( {\dfrac{1}{{x + \sqrt x }} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{\sqrt x }}{{x + 2\sqrt x  + 1}},$ với $x > 0.$

a) Rút gọn biểu thức: $A.$

Điều kiện: $x > 0.$

$\begin{array}{l}A = \left( {\dfrac{1}{{x + \sqrt x }} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{\sqrt x }}{{x + 2\sqrt x  + 1}}\\\;\;\; = \left( {\dfrac{1}{{\sqrt x \left( {\sqrt x  + 1} \right)}} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{\sqrt x }}{{{{\left( {\sqrt x  + 1} \right)}^2}}}\\\;\;\; = \dfrac{{1 - \sqrt x }}{{\sqrt x \left( {\sqrt x  + 1} \right)}}.\dfrac{{{{\left( {\sqrt x  + 1} \right)}^2}}}{{\sqrt x }}\\\;\;\; = \dfrac{{\left( {1 - \sqrt x } \right)\left( {\sqrt x  + 1} \right)}}{x}\\\;\;\; = \dfrac{{1 - x}}{x}.\end{array}$

b) Tìm các giá trị của $x$ để $A > \dfrac{1}{2}.$

Điều kiện: $x > 0.$

Ta có: $A > \dfrac{1}{2}$

$\begin{array}{l} \Leftrightarrow \dfrac{{1 - x}}{x} > \dfrac{1}{2}\\ \Leftrightarrow \dfrac{{1 - x}}{x} - \dfrac{1}{2} > 0\\ \Leftrightarrow \dfrac{{2 - 2x - x}}{{2x}} > 0\\ \Leftrightarrow 2 - 3x > 0\;\;\;\left( {do\;\;2x > 0\;\;\forall x > 0} \right)\\ \Leftrightarrow x < \dfrac{2}{3}.\end{array}$

Vậy với $0 < x < \dfrac{2}{3}$  thì $A > \dfrac{1}{2}.$

Bài 2:

1) Không dùng máy tính, trình bày cách giải hệ phương trình: $\left\{ \begin{array}{l}2x - y = 4\;\;\;\;\;\left( 1 \right)\\x + 3y =  - 5\;\;\;\;\left( 2 \right)\end{array} \right..$

Nhân cả 2 vế của phương trình $\left( 1 \right)$ với $3$ sau đó cộng vế với vế của hai phương trình với nhau để tìm $x.$  Sau đó thế giá trị vừa tìm được của $x$ vào phương trình $\left( 1 \right)$ để tìm $y.$

$\left\{ \begin{array}{l}2x - y = 4\\x + 3y =  - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x - 3y = 12\\x + 3y =  - 5\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}7x = 7\\y = 2x - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2.1 - 4\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}x = 1\\y =  - 2\end{array} \right..$

Vậy hệ phương trình có nghiệm duy nhất: $\left( {x;\;y} \right) = \left( {1; - 2} \right).$

2) Trong mặt phẳng tọa độ $Oxy$ đường thẳng $d$ có hệ số góc $k$ đi qua điểm $M\left( {1; - 3} \right)$ cắt các trục $Ox,\;\;Oy$ lần lượt tại $A$ và $B.$

a) Xác định tọa độ các điểm A, B theo k.

Gọi phương trình đường thẳng d có hệ số góc k là: $y = kx + b$

Đường thẳng d đi qua điểm $M\left( {1; - 3} \right)$  nên ta có: $- 3 = k.1 + b \Leftrightarrow b =  - k - 3$

Khi đó phương trình đường thẳng d có dạng: $y = kx - k - 3$

Nếu $k = 0 \Rightarrow d:y =  - 3$ nên điểm M không thuộc vào đường thẳng d trái với giả thiết.  Khi đó ta suy ra $k \ne 0.$

+) Đường thẳng d giao với trục Ox (Phương trình y = 0 ) tại điểm A:

Khi đó ta có tọa độ điểm A là nghiệm của hệ phương trình: $\left\{ \begin{array}{l}y = 0\\y = kx - k - 3\end{array} \right.$

$\Leftrightarrow\left\{ \begin{array}{l}y = 0\\x = \dfrac{{k + 3}}{k}\end{array} \right. \Rightarrow A\left( {\dfrac{{k + 3}}{k};0} \right)$

+) Đường thẳng d giao với trục Oy (phương trình x = 0) tại điểm B:

Khi đó tọa độ điểm B chính là nghiệm của hệ phương trình:

$\left\{ \begin{array}{l}x = 0\\y = kx - k - 3\end{array} \right.\left\{ \begin{array}{l}x = 0\\y =  - k - 3\end{array} \right.$ $\Rightarrow B\left( {0; - k - 3} \right)$

b) Tính diện tích tam giác OAB khi k = 2

Khi k = 2 ta có tọa độ của các điểm A, B là: $A\left( {\dfrac{5}{2};0} \right);\;\;B\left( {0; - 5} \right)$

$OA = \left| {\dfrac{5}{2}} \right| = \dfrac{5}{2};OB = \left| { - 5} \right| = 5$

Ta có tam giác OAB vuông tại A khi đó ${S_{OAB}} = \dfrac{1}{2}OA.OB = \dfrac{1}{2}.\dfrac{5}{2}.5 = \dfrac{{25}}{4}\left( {dvdt} \right)$

Vậy khi k = 2 thì ta có: ${S_{OAB}} = \dfrac{{25}}{4}\left( {dvdt} \right)$

Bài 3.

Gọi số có hai chữ số cần tìm là: $\overline {ab} \left( {a \in {{\rm N}^*},b \in {\rm N},\;\;0 < a \le 9,\;0 \le b \le 9} \right).$

Số đảo ngược của số  ban đầu là: $\overline {ba} \;\;\left( {b \ne 0} \right)$

Theo đề bài, hiệu của số ban đầu với số đảo ngược của nó bằng 18 nên ta có:

$\begin{array}{l}\overline {ab}  - \overline {ba}  = 18\,\,\\ \Leftrightarrow 10a + b - \left( {10b + a} \right) = 18\\ \Leftrightarrow 10a + b - 10b - a = 18\\ \Leftrightarrow a - b = 2\,\,\,\left( 1 \right)\end{array}$

Tổng của số ban đầu với bình phương số đảo ngược của nó bằng 618 nên ta có:

$\begin{array}{l}\overline {ab}  + {\left( {\overline {ba} } \right)^2} = 618\\ \Leftrightarrow 10a + b + {\left( {10b + a} \right)^2} = 618\\ \Leftrightarrow 10a + b + 100{b^2} + 20ab + {a^2} = 618\,\,\,\left( 2 \right)\end{array}$

Từ (1) và (2) ta có hệ phương trình:

$\begin{array}{l}\left\{ \begin{array}{l}a - b = 2\\10a + b + 100{b^2} + 20ab + {a^2} = 618\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = b + 2\\10\left( {b + 2} \right) + b + 100{b^2} + 20\left( {b + 2} \right)b + {\left( {b + 2} \right)^2} = 618\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = b + 2\\10b + 20 + b + 100{b^2} + 20{b^2} + 40b + {b^2} + 4b + 4 = 618\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}a = b + 2\\121{b^2} + 55b - 594 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = b + 2\\\left[ \begin{array}{l}b = 2\left( {tm} \right)\\b =  - \dfrac{{27}}{{11}}\left( {ktm} \right)\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}b = 2\\a = 4\left( {tm} \right)\end{array} \right.\end{array}$

Vậy số cần tìm là: 42.

Bài 4.

Cho tam giác đều ABC có đường cao AH. Trên cạnh BC lấy điểm M tùy ý (M không trùng với B, C, H). Gọi P, Q lần lượt là hình chiếu vuông góc vủa M lên AB và AC.

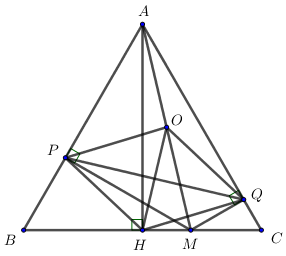
a) Chứng minh tứ giác APMQ nội tiếp được trong đường tròn và xác định tâm O của đường tròn này.

Xét tứ giác APMQ có: $\angle APM = \angle AQM = {90^0}\,\,\left( {gt} \right)$

$\Rightarrow \angle APM + \angle AQM = {180^0} \Rightarrow$ Tứ giác APMQ là tứ giác nội tiếp đường tròn đường kính AM.

Gọi O là trung điểm của AM $\Rightarrow$ tứ giác APMQ nội tiếp được trong đường tròn tâm O đường kính AM.

b) Chứng minh $OH \bot PQ$.

Ta có $\angle AHM = {90^0}\,\,\left( {gt} \right)$

$\Rightarrow \angle AHM$ nội tiếp chắn nửa đường tròn đường kính AM $\Rightarrow$ H thuộc đường tròn $\left( O \right)$.

Ta có $\angle HPQ = \angle HAC$ (hai góc nội tiếp cùng chắn cung HQ)

$\angle HQP = \angle HAB$ (hai góc nội tiếp cùng chắn cung HP).

Mà $\angle HAC = \angle HAB$ (tam giác ABC đều nên đường cao AH đồng thời là đường phân giác)

$\Rightarrow \angle HPQ = \angle HQP \Rightarrow \Delta HPQ$ cân tại H $\Rightarrow HP = HQ\,\,\left( 1 \right)$.

Mà $OP = OQ$ (do P, Q đều thuộc $\left( O \right)$)  (2).

Từ (1) và (2) $\Rightarrow OH$ là trung trực của PQ.

$\Rightarrow OH \bot PQ$.

c) Chứng minh $MP + MQ = AH$.

Ta có

$\begin{array}{l}{S_{\Delta MAB}} = \dfrac{1}{2}MP.AB = \dfrac{1}{2}MP.BC\,\,\left( {Do\,\,AB = BC} \right)\\{S_{\Delta MAC}} = \dfrac{1}{2}MQ.AC = \dfrac{1}{2}MQ.BC\,\,\left( {Do\,\,AC = BC} \right)\\{S_{\Delta ABC}} = \dfrac{1}{2}AH.BC\end{array}$

Mà ${S_{\Delta MAB}} + {S_{\Delta MAC}} = {S_{\Delta ABC}}$

$\begin{array}{l} \Rightarrow \dfrac{1}{2}MP.BC + \dfrac{1}{2}MQ.BC = \dfrac{1}{2}AH.BC\\ \Rightarrow \dfrac{1}{2}BC\left( {MP + MQ} \right) = \dfrac{1}{2}AH.BC\\ \Rightarrow MP + MQ = AH\,\,\left( {dpcm} \right)\end{array}$

Bài  5:

Cho tam giác đều ABC có cạnh bằng a. Hai điểm M, N lần lượt di động trên hai đoạn thẳng AB, AC sao cho $\dfrac{{AM}}{{MB}} + \dfrac{{AN}}{{NC}} = 1$. Đặt $AM = x;\,\,AN = y$.

Chứng minh $MN = a - x - y$

Ta có:

$\begin{array}{l}\,\,\,\,\,\dfrac{{AM}}{{MB}} + \dfrac{{AN}}{{NC}} = 1\\ \Rightarrow \dfrac{{AM}}{{AB - AM}} + \dfrac{{AN}}{{AC - AN}} = 1\\ \Leftrightarrow \dfrac{x}{{a - x}} + \dfrac{y}{{a - y}} = 1\\ \Leftrightarrow ax - xy + ay - xy = {a^2} - ax - ay + xy\\ \Leftrightarrow {a^2} - 2ax - 2ay + 3xy = 0\\ \Leftrightarrow {a^2} + {x^2} + {y^2} - 2ax - 2by + 2xy = {x^2} + {y^2} - xy\\ \Leftrightarrow {\left( {a - x - y} \right)^2} = {x^2} + {y^2} - xy\end{array}$

Giả sử $x > y$ , kẻ MM’ // BC, NN’ // BC $M' \in AC;\,\,N' \in AB$.

Áp dụng định lí Ta-let ta có $\dfrac{{AM}}{{AB}} = \dfrac{{AM'}}{{AC}};\,\,AB = AC \Rightarrow AM = AM'$

$\angle BAC = {60^0} \Rightarrow \angle MAM' = {60^0} \Rightarrow \Delta AMM'$ đều $\Rightarrow MM' = AM = x$.

Chứng minh tương tự ta có : $NN' = y$

MM’ // NN’ ; $\angle AMM' = \angle AM'M = {60^0} \Rightarrow$ tứ giác MM’NN’ là hình thang cân.

Ta có $MN' = M'N = x - y$.

Kẻ $NH \bot MM'$ ta có : $M'H = \dfrac{{x - y}}{2};\,\,MH = \dfrac{{x + y}}{2}$.

Áp dụng định lí Pitago trong tam giác vuông NHM’ có :

$NH = \sqrt {NM{'^2} - M'{H^2}}$$\;= \sqrt {{{\left( {x - y} \right)}^2} - \dfrac{{{{\left( {x - y} \right)}^2}}}{4}}$$\;= \dfrac{{\left( {x - y} \right)\sqrt 3 }}{2}$

Áp dụng định lí Pitago trong tam giác vuông NHM có :

$\begin{array}{l}MN = \sqrt {N{H^2} + M{H^2}} \\ = \sqrt {\dfrac{{3{{\left( {x - y} \right)}^2}}}{4} + \dfrac{{{{\left( {x + y} \right)}^2}}}{4}}  \\= \sqrt {\dfrac{{4{x^2} + 4{y^2} - 4xy}}{4}}\\  = \sqrt {{x^2} + {y^2} - xy}  \\= \sqrt {{{\left( {a - x - y} \right)}^2}}  = \left| {a - x - y} \right|\end{array}$

Ta có

$\begin{array}{l}\dfrac{{AM}}{{MB}} + \dfrac{{AN}}{{NC}} = 1\\ \Rightarrow \dfrac{{AM}}{{MB}} < 1 \Rightarrow AM < MB\\ \Rightarrow AM + AM < AM + MB = AB = a\\ \Rightarrow AM < \dfrac{1}{2}a\end{array}$

Chứng minh tương tự ta có $AN < \dfrac{1}{2}a$

$\Rightarrow a - x - y > a - \dfrac{1}{2}a - \dfrac{1}{2}a = 0$

$\Rightarrow \left| {a - x - y} \right| = a - x - y$

Vậy $MN = a - x - y$.