Đề số 20 - Đề thi vào lớp 10 môn Toán
Đề thi vào lớp 10 môn Toán - Đề số 20 có đáp án và lời giải chi tiết
Đề bài
Câu 1. (2,0 điểm)
a) Giải phương trình: \({x^2} + x - 12 = 0.\)
b) Giải hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 6\\2x + y = 2\end{array} \right.\)
Câu 2 (2,0 điểm) Cho parabol: \(y = 3{x^2}\) và đường thẳng \(d:\,\,y = x + m - 1\) (với m là tham số).
a) Vẽ parabol (P).
b) Tìm tất cả các giá trị của m để (P) cắt (d) tại đúng một điểm.
Câu 3 (1,5 điểm). Một mảnh vườn hình chữ nhật có chiều dài hơn chiều rộng 5m. Nếu tăng chiều dài thêm 10m và chiều rộng thêm 5m thì diện tích mảnh vườn đó tăng gấp đôi. Tính chiều dài và chiều rộng mảnh vườn đó.
Câu 4 (3,5 điểm). Cho tam giác ABC vuông tại A, M là trung điểm của cạnh AC. Vẽ đường tròn đường kính MC cắt cạnh BC tại N \(\left( {N \ne C} \right).\) Đường thẳng BM cắt đường tròn đường kính MC tại D \(\left( {D \ne M} \right).\) Chứng minh:
a) Tứ giác BADC nội tiếp được trong một đường tròn. Xác định tâm O của đường tròn đó.
b) \(CM.CA = CN.CB.\)
c) \(O{M^2} = ON.OC.\)
Câu 5 (1,0 điểm). Cho hai số dương x, y thỏa mãn \(xy = 2018.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{2}{x} + \dfrac{{1009}}{y} - \dfrac{{2018}}{{2018x + 4y}}.\)
Lời giải chi tiết
Câu 1. (2,0 điểm)
a) Giải phương trình: \({x^2} + x - 12 = 0.\)
Ta có: \(\Delta = 1 + 48 = 49 > 0 \Rightarrow \sqrt \Delta = 7\)
Khi đó phương trình đã cho có hai nghiệm phân biệt: \({x_1} = \dfrac{{ - 1 - 7}}{2} = - 4;{x_1} = \dfrac{{ - 1 + 7}}{2} = 3\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ { - 4;3} \right\}\)
b) Giải hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 6\\2x + y = 2\end{array} \right.\)
\(\left\{ \begin{array}{l}x - 2y = 6\\2x + y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - 4y = 12\\2x + y = 2\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l} - 5y = 10\\x = 6 + 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = - 2\\x = 6 + 2.\left( { - 2} \right)\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}y = - 2\\x = 2\end{array} \right.\)
Vậy hệ phương trình có nghiệm là: \(\left( {x;y} \right) = \left( {2; - 2} \right)\)
Câu 2 (2,0 điểm)
Cho parabol: \(y = 3{x^2}\) và đường thẳng \(d:\,\,y = x + m - 1\) ( với m là tham số).
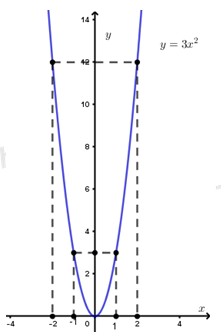
a) Vẽ parabol (P).
Bảng giá trị
|
\(x\) |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
\(y = 3{x^2}\) |
\(12\) |
3 |
0 |
3 |
12 |
Vậy parabol (P) đi qua các điểm có tọa độ tương ứng là: \(\left( { - 2;12} \right);\left( { - 1;3} \right);\left( {0;0} \right);\left( {1;3} \right);\left( {2;12} \right)\)
b) Tìm tất cả các giá trị của m để (P) cắt (d) tại đúng một điểm.
Phương trình hoành độ giao điểm của (P) và (d) là: \(3{x^2} - x - m + 1 = 0\,\,\left( 1 \right)\)
Số giao điểm của (P) và (d) cũng chính là số nghiệm của phương trình (1).
(P) cắt (d) tại đúng một điểm khi và chỉ khi phương trình (1) có nghiệm kép \( \Leftrightarrow \Delta = 0 \)
\(\Leftrightarrow 1 - 12\left( { - m + 1} \right) = 0 \Leftrightarrow m = \dfrac{{11}}{{12}}\)
Vậy với \(m = \dfrac{{11}}{{12}}\) thì (P) cắt (d) tại đúng một điểm.
Câu 3 (1,5 điểm).
Gọi chiều rộng của hình chữ nhật là x (m) (x > 0)
Chiều dài của hình chữ nhật là: x + 5 (m)
Diện tích ban đầu của hình chữ nhật là: \(x\left( {x + 5} \right)\,\,\left( {{m^2}} \right)\)
Tăng chiều dài thêm 10m, chiều rộng thêm 5m thì ta có chiều dài và chiều rộng sau khi thay đổi lần lượt là: \(x + 5 + 10\left( m \right);x + 5\left( m \right)\) .
Diện tích của hình chữ nhật sau khi thay đổi là: \(\left( {x + 15} \right)\left( {x + 5} \right)\left( {{m^2}} \right)\)
Theo bài ra ta có phương trình:
\(\begin{array}{l}\left( {x + 15} \right)\left( {x + 5} \right) = 2x\left( {x + 5} \right)\\ \Leftrightarrow {x^2} + 20x + 75 = 2{x^2} + 10x\\ \Leftrightarrow {x^2} - 10x - 75 = 0\\ \Leftrightarrow {x^2} + 5x - 15x - 75 = 0\\ \Leftrightarrow \left( {x + 5} \right)\left( {x - 15} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = - 5\left( {ktm} \right)\\x = 15\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy chiều rộng của hình chữ nhật là 15m; chiều dài của hình chữ nhật là: 20m.
Câu 4 (3,5 điểm). Cho tam giác ABC vuông tại A, M là trung điểm của cạnh AC. Vẽ đường tròn đường kính MC cắt cạnh BC tại N \(\left( {N \ne C} \right).\) Đường thẳng BM cắt đường tròn đường kính MC tại D \(\left( {D \ne M} \right).\) Chứng minh:

a) Tứ giác BADC nội tiếp được trong một đường tròn. Xác định tâm O của đường tròn đó.
Ta có: D thuộc đường tròn đường kính MC nên \(\angle MDC = {90^0}\,\,hay\,\,\angle BDC = {90^0}\)
Nên D thuộc đường tròn đường kính BC (1)
Có: \(\angle BAC = {90^0}\) (gt tam giác ABC vuông tại A) nên A thuộc đường tròn đường kính BC. (2)
Từ (1) và (2) suy ra 4 điểm B, A,D, C cùng thuộc đường tròn đường kính BC.
Hay tứ giác BADC nội tiếp đường tròn đường kính BC.
Gọi O là trung điểm của BC, Khi đó ta có tâm O của đường tròn chính là trung điểm của BC và bán kính chính bằng nửa độ dài BC.
b) \(CM.CA = CN.CB.\)
Xét tam giác CMN và tam giác CBA có:
\(\angle CNM = \angle CAB = {90^0}\)
\(\angle NCM\) chung
Nên \(\Delta CMN \sim \Delta CBA\left( {g - g} \right)\)
\( \Rightarrow \dfrac{{CM}}{{CB}} = \dfrac{{CN}}{{CA}}\)
\(\Rightarrow CM.CA = CB.CN\) (điều phải chứng minh)
c) \(O{M^2} = ON.OC.\)
Ta có: O là trung điểm của BC (cm câu a)
M là trung điểm của AC (gt)
Nên OM là đường trung bình của tam giác ABC
Khi đó ta có: \(OM\parallel AB\) . Mà \(AB \bot AC\left( {gt} \right)\)
\(\Rightarrow OM \bot AC\,\,hay\,\,\,OM\,\,\, \bot MC\)
Xét tam giác vuông OMC có MN là đường cao.
\( \Rightarrow O{M^2} = ON.OC\) (điều phải chứng minh)
Câu 5 (1,0 điểm). Cho hai số dương x, y thỏa mãn \(xy = 2018.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{2}{x} + \dfrac{{1009}}{y} - \dfrac{{2018}}{{2018x + 4y}}.\)
Cách giải:
Áp dung bất đẳng thức Cauchy cho hai số dương: \(\dfrac{2}{x};\dfrac{{1009}}{y}\) ta có:
\(\dfrac{2}{x} + \dfrac{{1009}}{y} \ge 2\sqrt {\dfrac{2}{x}.\dfrac{{1009}}{y}} = 2\sqrt {\dfrac{{2018}}{{2018}}} = 2\) (1)
Áp dụng bất đẳng thức Cauchy cho hai số dương: \(2018x;4y\) ta có:
Khi đó ta có: \(\dfrac{{2018}}{{2018x + 4y}} \le \dfrac{{2018}}{{8072}} = \dfrac{1}{4}\)
\(\Rightarrow \dfrac{{2018}}{{2018x + 4y}} \ge - \dfrac{1}{4}\)
\(P = \dfrac{2}{x} + \dfrac{{1009}}{y} - \dfrac{{2018}}{{2018x + 4y}} \ge 2 - \dfrac{1}{4} = \dfrac{7}{4}\)
Vậy \({P_{\min }} = \dfrac{7}{4}\) . Dấu “=” xảy ra khi và chỉ khi: \(\left\{ \begin{array}{l}x = 2\\y = 1009\end{array} \right.\)