Đề số 19 - Đề kiểm tra học kì 1 - Toán 9 — Không quảng cáo

Đề bài

Phần I: Trắc nghiệm khách quan (2,0 điểm)

Học sinh ghi đáp án đúng là A, B, C hoặc D vào tờ giấy thi

1 . Điều kiện xác định của biểu thức$\sqrt {6 - 3x}$ là:

A. $x \le 2$ B. $x \ge 2$

C. $x \ge 0$ D. $x < 2$

2 . Giá trị nhỏ nhất của biểu thức $p = \sqrt {x + 3}  - 1$ là:

A. $3$ B. $- 1$

C. $- 3$ D. $0$

3 . Giá trị biểu thức $P = \dfrac{{\sqrt x  - 3}}{{\sqrt x  + 3}}$khi $x = 4 - 2\sqrt 3$ là:

A. $- 11 + 6\sqrt 3$ B. $\dfrac{{ - 11 - 6\sqrt 3 }}{{13}}$

C. $\dfrac{{ - 5 - 12\sqrt 3 }}{{37}}$ D. $1$

4 . Cho tam giác ABC vuông tại A . Biết rằng $\dfrac{{AB}}{{AC}} = \sqrt 3$. Số đo độ của góc ABC bằng:

A. ${30^0}$ B. ${60^0}$

C. ${45^0}$ D. ${50^0}$

5 . Với giá trị nào của a thì hàm số $y = \left( {a - 5} \right)x + 1$ đồng biến trên tập$\mathbb{R}$?

A. $a < 5$ B. $a > 5$

C. $a = 5$ D. $a >  - 5$

6 . Cho hai đường thẳng$\left( {{d_1}} \right)$$:\,\,y = 2x + 3$ và$\left( {{d_2}} \right)$$:\,\,y = \left( {{m^2} + 1} \right)x + m + 2$ (với m là tham số). Với giá trị nào của tham số m thì đường thẳng $\left( {{d_1}} \right)$ song song với đường thẳng $\left( {{d_2}} \right)$?

A. $m = 2$

B. $m = 1$ hoặc$m =  - 1$

C. $m = 1$

D. $m =  - 1$

7 . Cho EM, EN là hai tiếp tuyến của đường tròn $\left( O \right)$ với tiếp điểm M, N . Khẳng định nào sau đây là sai:

A. $\angle EMO = {90^o}$

B. Bốn điểm E, M, O, N cùng thuộc một đườngtròn

C. MN là trung trực của EO

D. OE là phân giác của$\angle MON$

8 . Hai đường tròn $\left( {O;5} \right)$và $\left( {O';8} \right)$ có vị trí tương đối với nhau như thế nào biết $OO' = 12$

A. Tiếp xúc nhau

B. Không giao nhau

C. Tiếp xúc ngoài

D. Cắt nhau

Phần II: Tự luận (8,0 điểm)

Câu 1 (2,0 điểm): Cho hai biểu thức $A = \dfrac{{2\sqrt x }}{{\sqrt x  + 3}} + \dfrac{{\sqrt x }}{{\sqrt x  - 3}} - \dfrac{{3x + 3}}{{x - 9}}$và $B = \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 3}}$ với $x \ge 0\,,\,\,x \ne 9$

1) Rút gọn biểu thức A .

2) Tìm tất cả các giá trị của x để $\dfrac{A}{B} <  - \dfrac{1}{2}$.

Câu 2 (2,5 điểm): Trong mặt phẳng tọa độ Oxy , cho đường thẳng $\left( d \right)$$:\,\,y = ax + 3$.

1) Xác định a biết $\left( d \right)$ đi qua $K\left( {1; - 1} \right)$. Vẽ đồ thị với a vừa tìm được.

2) Tìm tất cả các giá trị của a để đường thẳng $\left( d \right)$ cắt Ox và Oy lần lượt tại hai điểm M và N sao cho diện tích tam giác OMN bằng 4.

Câu 3 (3,0 điểm): Cho đường tròn $\left( {O;R} \right)$. Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF đến đường tròn (với E, F là các tiếp điểm).

1) Chứng minh các điểm M, E, O, F cùng thuộc một đường tròn.

2) Đoạn OM cắt đường tròn $\left( {O;R} \right)$ tại I . Chứng minh I là tâm đường tròn nội tiếp tam giác MEF .

3) Kẻ đường kính ED của $\left( {O;R} \right)$. Hạ FK vuông góc với ED . Gọi P là giao điểm của MD và FK . Chứng minh P là trung điểm của FK .

Câu 4  (0,5 điểm): Giải phương trình ${x^2} + x - 17 = \sqrt {\left( {{x^2} - 15} \right)\left( {x - 3} \right)}  + \sqrt {{x^2} - 15}  + \sqrt {x - 3}$

LG trắc nghiệm

Lời giải chi tiết:

Phần I: Trắc nghiệm khách quan

1A	2B	3A	4A
5B	6D	7C	8D

LG bài 1

Lời giải chi tiết:

: Cho hai biểu thức $A = \dfrac{{2\sqrt x }}{{\sqrt x  + 3}} + \dfrac{{\sqrt x }}{{\sqrt x  - 3}} - \dfrac{{3x + 3}}{{x - 9}}$ và $B = \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 3}}$ với $x \ge 0\,,\,\,x \ne 9$

1) Rút gọn biểu thức A .

$\begin{array}{l}A = \dfrac{{2\sqrt x }}{{\sqrt x  + 3}} + \dfrac{{\sqrt x }}{{\sqrt x  - 3}} - \dfrac{{3x + 3}}{{x - 9}}\\ = \dfrac{{2\sqrt x .\left( {\sqrt x  - 3} \right) + \sqrt x .\left( {\sqrt x  + 3} \right) - \left( {3x + 3} \right)}}{{x - 9}}\\= \dfrac{{2x - 6\sqrt x  + x + 3\sqrt x  - 3x - 3}}{{x - 9}} \\= \dfrac{{ - 3\sqrt x  - 3}}{{x - 9}}.\end{array}$

2) Tìm tất cả các giá trị của x để $\dfrac{A}{B} <  - \dfrac{1}{2}$ .

$\begin{array}{l}\dfrac{A}{B} = \dfrac{{ - 3\sqrt x  - 3}}{{x - 9}}:\dfrac{{\sqrt x  + 1}}{{\sqrt x  - 3}} \\\;\;\;= \dfrac{{ - 3\sqrt x  - 3}}{{x - 9}}.\dfrac{{\sqrt x  - 3}}{{\sqrt x  + 1}} \\\;\;\;= \dfrac{{ - 3\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 3} \right)}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)\left( {\sqrt x  + 1} \right)}} \\\;\;\;= \dfrac{{ - 3}}{{\sqrt x  + 3}}\\\dfrac{A}{B} <  - \dfrac{1}{2} \Leftrightarrow \dfrac{{ - 3}}{{\sqrt x  + 3}} <  - \dfrac{1}{2} \\\Leftrightarrow \dfrac{3}{{\sqrt x  + 3}} > \dfrac{1}{2}\\ \Leftrightarrow 6 > \sqrt x  + 3 \Leftrightarrow \sqrt x  < 3 \Leftrightarrow x < 9.\end{array}$

Kết hợp điều kiện đầu bài $\Rightarrow$$0 \le x < 9.$

Vậy với mọi $0 \le x < 9$ thỏa mãn yêu cầu đề bài.

LG bài 2

Lời giải chi tiết:

1) Xác định a biết $\left( d \right)$ đi qua $K\left( {1; - 1} \right)$ . Vẽ đồ thị với a vừa tìm được.

$\left( d \right)$ đi qua $K\left( {1; - 1} \right)$$\Rightarrow  - 1 = a.1 + 3 \Leftrightarrow a =  - 4$

Vậy với $a =  - 4$ thì $\left( d \right)$ đi qua $K\left( {1; - 1} \right)$

Với $a =  - 4$ thì $\left( d \right)\,:\,\,y =  - 4x + 3$

Đường thẳng $\left( d \right)$ đi qua $K\left( {1; - 1} \right)$ và $H\left( {0;3} \right)$

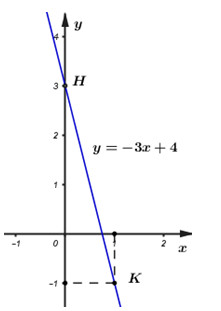
2) Tìm tất cả các giá trị của a để đường thẳng $\left( d \right)$ cắt Ox và Oy lần lượt tại hai điểm M và N sao cho diện tích tam giác OMN bằng 4.

Để đường thẳng $\left( d \right)$ cắt Ox và Oy lần lượt tại hai điểm M và N $\Leftrightarrow \,\,a \ne 0$

$M\left( {{x_M};{y_M}} \right)$ là giao điểm của đường thẳng $\left( d \right)$ và trục Ox

$\Rightarrow \left\{ \begin{array}{l}{y_M} = a{x_M} + 3\\{y_M} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} =  - \dfrac{3}{a}\\{y_M} = 0\end{array} \right.$

$\Rightarrow M\left( { - \dfrac{3}{a};0} \right) \Rightarrow OM = \left| { - \dfrac{3}{a}} \right| = \left| {\dfrac{3}{a}} \right|$

$N\left( {{x_N};{y_N}} \right)$ là giao điểm của đường thẳng $\left( d \right)$ và trục Oy

$\Rightarrow \left\{ \begin{array}{l}{y_N} = a{x_N} + 3\\{x_N} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_N} = 0\\{y_M} = 3\end{array} \right.$

$\Rightarrow N\left( {0;3} \right) \Rightarrow ON = 3$

Diện tích tam giác OMN bằng 4 $\Rightarrow {S_{\Delta OMN}} = \dfrac{1}{2}OM.ON = \dfrac{1}{2}.\left| {\dfrac{3}{a}} \right|.3 = \dfrac{9}{2}.\left| {\dfrac{1}{a}} \right| = 4$

$\Leftrightarrow \left| {\dfrac{1}{a}} \right| = \dfrac{8}{9} \Leftrightarrow \left| a \right| = \dfrac{9}{8} \Leftrightarrow \left[ \begin{array}{l}a = \dfrac{9}{8}\\a =  - \dfrac{9}{8}\end{array} \right.$

Vậy với $a = \dfrac{9}{8}$ hoặc $a =  - \dfrac{9}{8}$thỏa mãn yêu cầu đề bài.

LG bài 3

Lời giải chi tiết:

Cho đường tròn $\left( {O;R} \right)$ . Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF đến đường tròn (với E, F là các tiếp điểm).

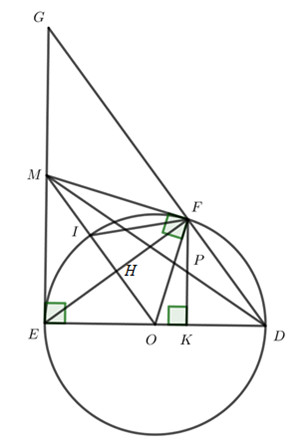
1) Chứng minh các điểm M, E, O, F cùng thuộc một đường tròn.

Vì ME là tiếp tuyến của $\left( O \right)$ nên ME vuông góc với OE , suy ra tam giác MOE nội tiếp đường tròn đường kính MO (1)

Vì MF là tiếp tuyến của $\left( O \right)$ nên MF vuông góc với OF , suy ra tam giác MOF nội tiếp đường tròn đường kính MO (2)

Từ (1) và (2) suy ra M, E, O, F cùng thuộc một đường tròn.

2) Đoạn OM cắt đường tròn $\left( {O;R} \right)$ tại I . Chứng minh I là tâm đường tròn nội tiếp tam giác MEF .

Gọi $MO \cap EF = \left\{ H \right\}$

Vì M là giao điểm của 2 tiếp tuyến ME và MF của $\left( O \right)$

$\Rightarrow ME = MF$ (tính chất) mà $OE = OF = R$ (gt)

$\Rightarrow$ MO là đường trung trực của EF

$\Rightarrow MO \bot EF$

$\Rightarrow \angle IFE + \angle OIF = {90^o}\,$

Vì $OI = OF = R$  nên tam giác OIF cân tại O

$\Rightarrow \angle OIF = \angle OFI$  mà  $\angle MFI + \angle OFI = {90^o}\,;\,\,\,\angle IFE + \angle OIF = {90^o}$

$\Rightarrow \angle MFI = \angle IFE$

$\Rightarrow$ FI là phân giác của $\angle MFE$   (1)

Vì M là giao điểm của 2 tiếp tuyến ME và MF của $\left( O \right)$

$\Rightarrow$ MI là phân giác của $\angle EMF$ (tính chất)   (2)

Từ (1) và (2) $\Rightarrow$ I là tâm đường tròn nội tiếp tam giác MEF (đpcm)

3) Kẻ đường kính ED của $\left( {O;R} \right)$ . Hạ FK vuông góc với ED . Gọi P là giao điểm của MD và FK . Chứng minh P là trung điểm của FK .

Gọi G là giao điểm của tia DF và tia EM .

Ta có $\angle EFD = {90^o}$(góc nội tiếp chắn nửa đường tròn)$\Rightarrow EF \bot DG$mà $EF \bot OM$ (cmt)

$\Rightarrow OM//DG$ (từ vuông góc đến song song)

Tam giác EDG có $OE = OD\,\,;\,\,OM//DG\,\, \Rightarrow ME = MG$(tính chất đường trung bình)

Áp dụng định lý Ta-let cho tam giác EDM có $PK//ME$ (cùng vuông góc với ED ) ta được:$\dfrac{{PK}}{{ME}} = \dfrac{{DP}}{{DM}}$     (3)

Áp dụng định lý Ta-let cho tam giác MDG có $PF//MG$ (cùng vuông góc với ED ) ta được:   $\dfrac{{PE}}{{MG}} = \dfrac{{DP}}{{DM}}$     (4)

Từ (3) và (4) suy ra   $\dfrac{{PK}}{{ME}} = \dfrac{{PF}}{{MG}}$  mà  $ME = MG$ (cmt)

$\Rightarrow PK = PF\,\, \Rightarrow$ P là trung điểm của FK .

LG bài 4

Lời giải chi tiết:

Câu 4: Giải phương trình ${x^2} + x - 17 = \sqrt {\left( {{x^2} - 15} \right)\left( {x - 3} \right)}  + \sqrt {{x^2} - 15}  + \sqrt {x - 3}$

Điều kiện xác định $\left\{ \begin{array}{l}{x^2} - 15 \ge 0\\x - 3 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x \ge \sqrt {15} \\x \le  - \sqrt {15} \end{array} \right.\\x \ge 3\end{array} \right. \Leftrightarrow x \ge \sqrt {15}$

$\begin{array}{l}\;\;\;\;{x^2} + x - 17 = \sqrt {\left( {{x^2} - 15} \right)\left( {x - 3} \right)}  + \sqrt {{x^2} - 15}  + \sqrt {x - 3} \\ \Leftrightarrow 2{x^2} + 2x - 34 = 2\sqrt {\left( {{x^2} - 15} \right)\left( {x - 3} \right)}  + 2\sqrt {{x^2} - 15}  + 2\sqrt {x - 3} \\ \Leftrightarrow {x^2} - 15 - 2\sqrt {\left( {{x^2} - 15} \right)\left( {x - 3} \right)}  + x - 3 + {x^2} - 15 - 2\sqrt {{x^2} - 15}  + 1 + x - 3 - 2\sqrt {x - 3}  + 1 = 0\\ \Leftrightarrow {\left[ {\sqrt {{x^2} - 15}  - \sqrt {x - 3} } \right]^2} + {\left[ {\sqrt {{x^2} - 15}  - 1} \right]^2} + {\left[ {\sqrt {x - 3}  - 1} \right]^2} = 0\end{array}$

Ta thấy: ${\left[ {\sqrt {{x^2} - 15}  - \sqrt {x - 3} } \right]^2} \ge 0$ với mọi $x \ge \sqrt {15}$

${\left[ {\sqrt {{x^2} - 15}  - 1} \right]^2} \ge 0$ với mọi $x \ge \sqrt {15}$

${\left[ {\sqrt {x - 3}  - 1} \right]^2} \ge 0$ với mọi $x \ge \sqrt {15}$

Vậy phương trình có nghiệm $\Leftrightarrow {\left[ {\sqrt {{x^2} - 15}  - \sqrt {x - 3} } \right]^2} = {\left[ {\sqrt {{x^2} - 15}  - 1} \right]^2} = {\left[ {\sqrt {x - 3}  - 1} \right]^2} = 0$

Dấu “=” xảy ra $\Leftrightarrow \sqrt {{x^2} - 15}  = \sqrt {x - 3}  = 1 \Leftrightarrow {x^2} - 15 = x - 3 = 1 \Leftrightarrow x = 4$(tmđk)

Vậy nghiệm của phương trình là $x = 4$