Đề số 18 - Đề kiểm tra học kì 1 - Toán 9
Tải vềĐáp án và lời giải chi tiết Đề số 18 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 9
Đề bài
Câu 1 (2 điểm):
Cho \(A = \left( {\dfrac{{x + \sqrt x + 10}}{{x - 9}} + \dfrac{1}{{3 - \sqrt x }}} \right):\dfrac{1}{{\sqrt x - 3}}\)và \(B = \sqrt x + 1\) (với \(x \ge 0;\,\,x \ne 9\))
a) Tính giá trị của biểu thức B khi \(x = 16\)
b) Rút gọn A
c) Tìm giá trị của x để \(A > B\)
Câu 2 (2 điểm):
Cho đường thẳng \(\left( d \right)\) có phương trình \(y = \left( {2k - 1} \right)x + k - 2\)(với k là tham số)
a) Tìm giá trị của k biết đường thẳng \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right)\) có phương trình \(y = - 3x + 5\)
b) Với giá trị của k tìm được ở câu a, vẽ đường thẳng \(\left( d \right)\) trên mặt phẳng tọa độ và tính khoảng cách từ gốc tọa độ O đến đường thẳng \(\left( d \right)\)
Câu 3 (2điểm): Giải phương trình
a) \(\sqrt {x + 3} + \sqrt {16x + 48} = 6 + \sqrt {9x + 27} \)
b) \(\sqrt {4x + 1} = x - 1\)
Câu 4 (3,5 điểm): Cho đường tròn \(\left( {O,R} \right)\). Đường thẳng d không qua O cắt \(\left( O \right)\) tại hai điểm A và B . Điểm C thuộc tia đối của tia AB . Vẽ CE và CF là các tiếp tuyến của \(\left( O \right)\) ( E, F là hai tiếp điểm). Gọi H là trung điểm của AB .
a) Chứng minh 4 điểm C, E, O, H cùng thuộc một đường tròn.
b) Gọi CO cắt EF tại K . Chứng minh \(OK.OC = {R^2}\)
c) Đoạn thẳng CO cắt \(\left( O \right)\) tại I . Chứng minh I là tâm đường tròn nội tiếp tam giác CEF
d) Tìm vị trí điểm C trên tia đối của tia AB để tam giác CEF đều.
Câu 5 (0,5 điểm):
Cho \(0 < x < 1\). Tìm giá trị nhỏ nhất của biểu thức
\(M = \dfrac{x}{{1 - x}} + \dfrac{4}{x}\)
LG bài 1
Lời giải chi tiết:
a) Tính giá trị của biểu thức B khi \(x = 16\)
Với \(x = 16\) (tm) ta có \(B = \sqrt {16} + 1 = 4 + 1 = 5.\)
Vậy với \(x = 16\) thì \(B = 5\)
b) Rút gọn A
\(\begin{array}{l}A = \left( {\dfrac{{x + \sqrt x + 10}}{{x - 9}} + \dfrac{1}{{3 - \sqrt x }}} \right):\dfrac{1}{{\sqrt x - 3}} \\\;\;\;= \left[ {\dfrac{{x + \sqrt x + 10}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} - \dfrac{1}{{\sqrt x - 3}}} \right].\left( {\sqrt x - 3} \right)\\\;\;\; = \left[ {\dfrac{{x + \sqrt x + 10 - \left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}} \right].\left( {\sqrt x - 3} \right)\\\;\;\; = \dfrac{{x + 7}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}.\left( {\sqrt x - 3} \right)\\\;\;\; = \dfrac{{x + 7}}{{\sqrt x + 3}}\end{array}\)
c) Tìm giá trị của x để \(A > B\)
\(\begin{array}{l}A > B \Leftrightarrow \dfrac{{x + 7}}{{\sqrt x + 3}} > \sqrt x + 1\\ \Leftrightarrow x + 7 > \left( {\sqrt x + 1} \right)\left( {\sqrt x + 3} \right)\\ \Leftrightarrow x + 7 > x + 4\sqrt x + 3\\ \Leftrightarrow 4\sqrt x < 4 \Leftrightarrow x < 1\end{array}\)
Kết hợp điều kiện ta được \(0 \le x < 1\)thì \(A > B.\)
LG bài 2
Lời giải chi tiết:
a) Tìm giá trị của k biết đường thẳng \(\left( d \right)\) song song với đường thẳng \(\left( {d'} \right)\) có phương trình \(y = - 3x + 5\)
\(\left( d \right)//\left( {d'} \right) \Leftrightarrow \left\{ \begin{array}{l}2k - 1 = - 3\\k - 2 \ne 5\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}k = - 1\\k \ne 7\end{array} \right. \Leftrightarrow k = - 1\)
Vậy với \(k = - 1\) thỏa mãn yêu cầu đề bài.
b) Với giá trị của k tìm được ở câu a, vẽ đường thẳng \(\left( d \right)\) trên mặt phẳng tọa độ và tính khoảng cách từ gốc tọa độ O đến đường thẳng \(\left( d \right)\)
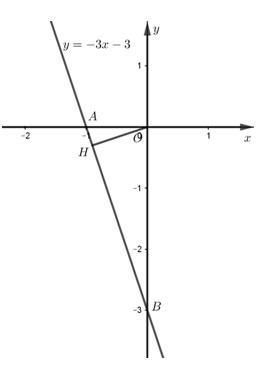
Khi \(k = - 1\) thì \(\left( d \right):y = - 3x - 3\)
Ta có bảng giá trị:
|
x |
0 |
-1 |
|
\(y = - 3x - 3\) |
-3 |
0 |
Vậy đồ thị hàm số \(y = - 3x - 3\) là đường thẳng đi qua hai điểm \(\left( {0; - 3} \right),\;\;\left( { - 1;\;0} \right).\)
Gọi A, B lần lượt là giao điểm của của \(\left( d \right)\) với Ox, Oy
Cho \(x = 0\) ta được \(y = - 3\)\( \Rightarrow B\left( {0; - 3} \right)\)\( \Rightarrow OB = 3\)
Cho \(y = 0\) ta được \(x = - 1\)\( \Rightarrow A\left( { - 1;0} \right)\)\( \Rightarrow OA = 1\)
Gọi H là hình chiếu của O trên \(\left( d \right)\), ta có:
\(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} = \dfrac{1}{1} + \dfrac{1}{{{3^2}}} = \dfrac{{10}}{9} \)
\(\Leftrightarrow OH = \dfrac{{3\sqrt {10} }}{{10}}\) (dvđd)
Vậy khoảng cách từ gốc tọa độ O đến đường thẳng \(\left( d \right)\) là \(OH = \dfrac{{3\sqrt {10} }}{{10}}\) (dvđd)
LG bài 3
Lời giải chi tiết:
a) \(\sqrt {x + 3} + \sqrt {16x + 48} = 6 + \sqrt {9x + 27} \). Điều kiện xác định: \(x \ge - 3\) .
\(\begin{array}{l} \Leftrightarrow \sqrt {x + 3} + \sqrt {16\left( {x + 3} \right)} = 6 + \sqrt {9\left( {x + 3} \right)} \\ \Leftrightarrow \sqrt {x + 3} + 4\sqrt {x + 3} = 6 + 3\sqrt {x + 3} \\ \Leftrightarrow 2\sqrt {x + 3} = 6\\ \Leftrightarrow \sqrt {x + 3} = 3\\ \Leftrightarrow x + 3 = 9 \Leftrightarrow x = 6\,\,\,\,\,\,(tm)\end{array}\)
Vậy phương trình có nghiệm là \(x = 6.\)
b) \(\sqrt {4x + 1} = x - 1\). Điều kiện xác định: \(x \ge - \dfrac{1}{4}\)
\( \Leftrightarrow \left\{ \begin{array}{l}x - 1 \ge 0\\4x + 1 = {x^2} - 2x + 1\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\{x^2} - 6x = 0\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\\left[ \begin{array}{l}x = 0\,\,\,\\x = 6\,\,\,\end{array} \right.\end{array} \right. \Leftrightarrow x = 6.\)
Vậy phương trình có nghiệm \(x = 6.\)
LG bài 4
Lời giải chi tiết:
Cho đường tròn \(\left( {O,R} \right)\). Đường thẳng d không qua O cắt \(\left( O \right)\) tại hai điểm A và B . Điểm C thuộc tia đối của tia AB . Vẽ CE và CF là các tiếp tuyến của \(\left( O \right)\) ( E, F là hai tiếp điểm). Gọi H là trung điểm của AB .
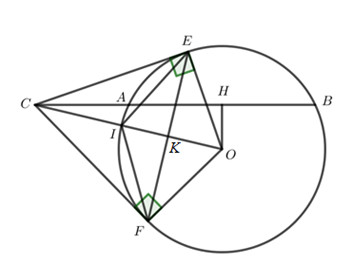
a) Chứng minh 4 điểm C, E, O, H cùng thuộc một đường tròn.
Vì H là trung điểm của dây cung AB của \(\left( O \right)\) nên OH vuông góc với AB , suy ra tam giác COH nội tiếp đường tròn đường kính CO (1)
Vì CE là tiếp tuyến của \(\left( O \right)\) nên CE vuông góc với OE , suy ra tam giác COE nội tiếp đường tròn đường kính CO (2)
Từ (1) và (2) suy ra C, E, O, H cùng thuộc đường tròn đường kính CO .
b) Gọi CO cắt EF tại K . Chứng minh \(OK.OC = {R^2}\)
Vì C là giao điểm của 2 tiếp tuyến CE và CF của \(\left( O \right)\)
\( \Rightarrow CE = CF\) (tính chất) mà \(OE = OF = R\) (gt)
\( \Rightarrow \) CO là đường trung trực của EF
\( \Rightarrow CO \bot EF\)
Xét tam giác vuông CEO đường cao EK ta có:
\(OK.OC = O{E^2} = {R^2}\) (đpcm)
c) Đoạn thẳng CO cắt \(\left( O \right)\) tại I . Chứng minh I là tâm đường tròn nội tiếp tam giác CEF
Vì \(OI = OF = R\) nên tam giác OIE cân tại O
\( \Rightarrow \angle OIF = \angle OFI\) mà \(\angle CFI + \angle OFI = {90^o}\,;\,\,\,\angle IFK + \angle OIF = {90^o}\)
\( \Rightarrow \angle CFI = \angle IFK\) (tính chất bắc cầu)
\( \Rightarrow \) FI là phân giác của \(\angle CFE\) (3)
Vì C là giao điểm của 2 tiếp tuyến CE và CF của \(\left( O \right)\)
\( \Rightarrow \) CI là phân giác của \(\angle ECF\) (tính chất) (4)
Từ (3) và (4) \( \Rightarrow \) I là tâm đường tròn nội tiếp tam giác CEF (đpcm)
d) Tìm vị trí điểm C trên tia đối của tia AB để tam giác CEF đều
Tam giác CEF đều \( \Rightarrow \angle ECF = {60^o}\)
Mà CI là phân giác của \(\angle ECF\)(cmt) \( \Rightarrow \angle FCO = {30^o}\)
Có tam giác FCO vuông tại F có \(\angle FCO = {30^o}\)
\( \Rightarrow OC = 2OF = 2R\)
Vậy điểm C trên tia đối của tia AB sao cho \(OC = 2R\) thì tam giác CEF đều.
Câu 5:
Cho \(0 < x < 1\). Tìm giá trị nhỏ nhất của biểu thức\(M = \dfrac{x}{{1 - x}} + \dfrac{4}{x}\)
Ta có: \(M = \dfrac{x}{{1 - x}} + \dfrac{4}{x} = \dfrac{x}{{1 - x}} + \dfrac{{4 - 4x + 4x}}{x} \)\(\,= \dfrac{x}{{1 - x}} + \dfrac{{4\left( {1 - x} \right)}}{x} + 4\)
Vì \(0 < x < 1 \Rightarrow 1 - x > 0 \Rightarrow \)\(\dfrac{x}{{1 - x}} > 0\) và \(\dfrac{{4\left( {1 - x} \right)}}{x} > 0\)
Áp dụng bất đẳng thức Cô-si cho hai số không âm \(\dfrac{x}{{1 - x}}\)và \(\dfrac{{4\left( {1 - x} \right)}}{x}\) ta có:
\(\begin{array}{l}\dfrac{x}{{1 - x}} + \dfrac{{4\left( {1 - x} \right)}}{x} \ge 2\sqrt {\dfrac{x}{{1 - x}}.\dfrac{{4\left( {1 - x} \right)}}{x}} = 4\\ \Leftrightarrow \dfrac{x}{{1 - x}} + \dfrac{{4\left( {1 - x} \right)}}{x} + 4 \ge 8 \Leftrightarrow M \ge 8\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow \dfrac{x}{{1 - x}} = \dfrac{{4\left( {x - 1} \right)}}{x}\)
\(\Leftrightarrow {x^2} = 4{\left( {x - 1} \right)^2} \)
\(\Leftrightarrow \left[ \begin{array}{l}x = 2x - 2\\x = - 2x + 2\end{array} \right.\)
\(\Leftrightarrow \left[ \begin{array}{l}x = 2\;\;\left( {ktm} \right)\\x = \dfrac{2}{3}\;\;\left( {tm} \right)\end{array} \right. \Leftrightarrow x = \dfrac{2}{3}\)
Vậy giá trị nhỏ nhất của M là 8 đặt được khi \(x = \dfrac{2}{3}.\)