Đề số 16 - Đề kiểm tra học kì 1 - Toán 9 — Không quảng cáo

Đề bài

Câu 1 (1,5 điểm): Thực hiện phép tính

a) $2\sqrt {50}  - 3\sqrt {32}  - \sqrt {162}  + 5\sqrt {98}$

b) $\sqrt {8 + 2\sqrt 7 }  + \sqrt {11 - 4\sqrt 7 }$

c) $\dfrac{{10}}{{\sqrt 5 }} + \dfrac{8}{{3 + \sqrt 5 }} - \dfrac{{\sqrt {18}  - 3\sqrt 5 }}{{\sqrt 2  - \sqrt 5 }}$

Câu 2  (2,0 điểm): Cho biểu thức $P = \left( {\dfrac{{2\sqrt x }}{{\sqrt x  + 3}} + \dfrac{{\sqrt x }}{{\sqrt x  - 3}} - \dfrac{{3x + 3}}{{x - 9}}} \right):\left( {\dfrac{{2\sqrt x  - 2}}{{\sqrt x  - 3}} - 1} \right)$, với $x \ge 0$và $x \ne 9$

a) Rút gọn P.

b) Tìm x để P đạt giá trị nhỏ nhất.

Câu 3 (1,5 điểm): Cho hàm số$y = 0,5x$ có đồ thị là $\left( {{d_1}} \right)$và hàm số $y =  - x + 3$ có đồ thị là $\left( {{d_2}} \right)$.

a) Vẽ $\left( {{d_1}} \right)$ và $\left( {{d_2}} \right)$ trên cùng một mặt phẳng tọa độ Oxy .

b) Xác định các hệ số a, b của đường thẳng $\left( {{d_3}} \right)$$:\,\,y = ax + b$. Biết $\left( {{d_3}} \right)$ song song với $\left( {{d_1}} \right)$ và $\left( {{d_3}} \right)$ cắt $\left( {{d_2}} \right)$ tại một điểm có hoành độ bằng 4.

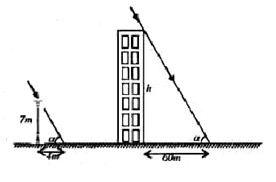
Câu 4 (4,5 điểm):1. Một cột đèn cao 7 m có bóng trên mặt đất 4 m . Cùng thời điểm đó, một tòa nhà cao tầng có bóng trên mặt đất là 60 m . Hãy cho biết tòa nhà đó cao bao nhiêu tầng, biết rằng mỗi tầng cao 3 m . (Hình vẽ minh họa)

2. Cho $\Delta ABC\,\,(AB < AC)$ nội tiếp đường tròn $\left( O \right)$có BC là đường kính, vẽ đường cao AH của $\Delta ABC$. $(H \in BC)$

a) Biết $AB = 6cm,\,\,AC = 8cm$. Tính độ dài AH và HB .

b) Tiếp tuyến tại A của $\left( O \right)$ cắt các tiếp tuyến tại B và C lần lượt tại M và N . Chứng minh $MN = MB + NC$ và $\angle MON = {90^o}$.

c) Trên cạnh AC lấy điểm E sao cho $AB = AE$, gọi I là trung điểm của BE . Chứng minh 3 điểm M, I, O thẳng hàng.

d) Chứng minh HI là tia phân giác của $\angle AHC$.

Câu 5  (0,5 điểm): Xe lăn cho người khuyết tật.

Với sự phát triển của khoa học kỹ thuật hiện nay, người ta tạo ra nhiều mẫu xe lăn đẹp và tiện dụng cho người khuyết tật. Công ty A đã sản xuất ra những chiếc xe lăn cho người khuyết tật với số vốn ban đầu là 500 triệu đồng ( dùng để mua nguyên vật liệu và thiết bị sản xuất ). Chi phí để sản xuất ra một chiếc xe lăn là 2,5 triệu đồng. Giá bán ra thị trường mỗi chiếc là 3 triệu đồng.

a) Em hãy viết hàm số biểu diễn tổng số tiền đã đầu tư đến khi sản xuất ra được x chiếc xe lăn ( gồm vốn ban đầu và chi phí sản xuất ) và hàm số biểu diễn số tiền thu được khi bán ra x chiếc xe lăn.

b) Công ty A phải bán bao nhiêu chiếc xe lăn với giá trên mới có thể thu hồi được đủ số tiền vốn đã đầu tư ban đầu? ( Gồm vốn ban đầu và chi phí sản xuất )

LG bài 1

Lời giải chi tiết:

Thực hiện phép tính

a) $2\sqrt {50}  - 3\sqrt {32}  - \sqrt {162}  + 5\sqrt {98}$$\; = 10\sqrt 2  - 12\sqrt 2  - 9\sqrt 2  + 35\sqrt 2  = 24\sqrt 2 .$

$\begin{array}{l}b)\;\sqrt {8 + 2\sqrt 7 }  + \sqrt {11 - 4\sqrt 7 }  \\= \sqrt {{{\left( {\sqrt 7  + 1} \right)}^2}}  + \sqrt {{{\left( {\sqrt 7  - 2} \right)}^2}}\\  = \left| {\sqrt 7  + 1} \right| + \left| {\sqrt 7  - 2} \right|\\ = \sqrt 7  + 1 + \sqrt 7  - 2 = 2\sqrt 7  - 1.\end{array}$$\begin{array}{l}c)\;\dfrac{{10}}{{\sqrt 5 }} + \dfrac{8}{{3 + \sqrt 5 }} - \dfrac{{\sqrt {18}  - 3\sqrt 5 }}{{\sqrt 2  - \sqrt 5 }}\\ = 2\sqrt 5  + \dfrac{{8\left( {3 - \sqrt 5 } \right)}}{{9 - 5}} - \dfrac{{3\left( {\sqrt 2  - \sqrt 5 } \right)}}{{\sqrt 2  - \sqrt 5 }}\\ = 2\sqrt 5  + 2\left( {3 - \sqrt 5 } \right) - 3 \\= 2\sqrt 5  + 6 - 2\sqrt 5  - 3 = 3\end{array}$

LG bài 2

Lời giải chi tiết:

Cho biểu thức $P = \left( {\dfrac{{2\sqrt x }}{{\sqrt x  + 3}} + \dfrac{{\sqrt x }}{{\sqrt x  - 3}} - \dfrac{{3x + 3}}{{x - 9}}} \right):\left( {\dfrac{{2\sqrt x  - 2}}{{\sqrt x  - 3}} - 1} \right)$ , với $x \ge 0$ và $x \ne 9$

a) Rút gọn P.

$\begin{array}{l}P = \left( {\dfrac{{2\sqrt x }}{{\sqrt x  + 3}} + \dfrac{{\sqrt x }}{{\sqrt x  - 3}} - \dfrac{{3x + 3}}{{x - 9}}} \right):\left( {\dfrac{{2\sqrt x  - 2}}{{\sqrt x  - 3}} - 1} \right)\\\;\;\; = \dfrac{{2\sqrt x \left( {\sqrt x  - 3} \right) + \sqrt x \left( {\sqrt x  + 3} \right) - \left( {3x + 3} \right)}}{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}}:\dfrac{{2\sqrt x  - 2 - \sqrt x  + 3}}{{\sqrt x  - 3}}\\\;\;\; = \dfrac{{2x - 6\sqrt x  + x + 3\sqrt x  - 3x - 3}}{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}}:\dfrac{{\sqrt x  + 1}}{{\sqrt x  - 3}} \\\;\;\;= \dfrac{{ - 3\left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}}.\dfrac{{\sqrt x  - 3}}{{\sqrt x  + 1}}\\\;\;\; = \dfrac{{ - 3}}{{\sqrt x  + 3}}\end{array}$

b) Tìm x để P đạt giá trị nhỏ nhất.

Ta có$\sqrt x  \ge 0 \Rightarrow \sqrt x  + 3 \ge 3 \Rightarrow \dfrac{1}{{\sqrt x  + 3}} \le \dfrac{1}{3} \Rightarrow \dfrac{{ - 3}}{{\sqrt x  + 3}} \ge \dfrac{{ - 3}}{3} =  - 1$

Dấu “=” xảy ra khi và chỉ khi $\sqrt x  = 0 \Leftrightarrow x = 0$ (tmđk)

Vậy ${P_{\min }} =  - 1 \Leftrightarrow x = 0$

LG bài 3

Lời giải chi tiết:

Cho hàm số $y = 0,5x$ có đồ thị là $\left( {{d_1}} \right)$ và hàm số $y =  - x + 3$ có đồ thị là $\left( {{d_2}} \right)$ .

a) Vẽ $\left( {{d_1}} \right)$ và $\left( {{d_2}} \right)$ trên cùng một mặt phẳng tọa độ Oxy .

x	0	2
$y = 0,5x$	0	1

$\Rightarrow \left( {{d_1}} \right)$ là đường thẳng đi qua gốc tọa độ và điểm $\left( {2;1} \right)$

x	0	3
$y =  - x + 3$	3	0

$\Rightarrow \left( {{d_2}} \right)$ là đường thẳng đi qua 2 điểm $\left( {0;3} \right)$ và $\left( {3;0} \right)$

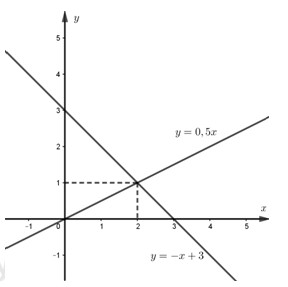
b) Xác định các hệ số a, b của đường thẳng $\left( {{d_3}} \right)$$:\,\,y = ax + b$ . Biết $\left( {{d_3}} \right)$ song song với $\left( {{d_1}} \right)$ và $\left( {{d_3}} \right)$ cắt $\left( {{d_2}} \right)$ tại một điểm có hoành độ bằng 4.

$\left( {{d_3}} \right)//\left( {{d_1}} \right) \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{2}\\b \ne 0\end{array} \right.\,\,\,\, \Rightarrow \,\,\left( {{d_3}} \right):\,\,y = \dfrac{1}{2}x + b$

Gọi $A\left( {4;{y_0}} \right)$ là giao điểm của $\left( {{d_3}} \right)$ và $\left( {{d_2}} \right)$

$A\left( {4;{y_0}} \right) \in \left( {{d_2}} \right) \Leftrightarrow {y_0} =  - 4 + 3 =  - 1 \Rightarrow A\left( {4; - 1} \right)$

$A\left( {4; - 1} \right) \in \left( {{d_3}} \right) \Leftrightarrow  - 1 = \dfrac{1}{2}.4 + b \Leftrightarrow  - 1 = 2 + b \Leftrightarrow b =  - 3$ (tmđk $b \ne 0$)

Vậy $\left( {{d_3}} \right):y = \dfrac{1}{2}x - 3$.

LG bài 4

Lời giải chi tiết:

1. Một cột đèn cao 7 m có bóng trên mặt đất 4 m . Cùng thời điểm đó, một tòa nhà cao tầng có bóng trên mặt đất là 60 m . Hãy cho biết tòa nhà đó cao bao nhiêu tầng, biết rằng mỗi tầng cao 3 m . (Hình vẽ minh họa)

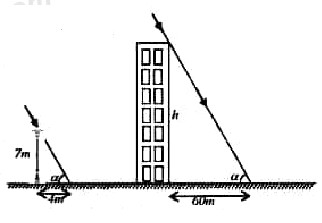
Gọi h là chiều cao tòa nhà cần tìm, $\alpha$là góc tia nắng mặt trời tạo với mặt đáy lúc ấy.

Khi đó ta có: $\tan \alpha  = \dfrac{7}{4} = \dfrac{h}{{60}} \Rightarrow h = 105\,\,(m)$

Vậy tòa nhà có$105:3 = 35$ (tầng)

2. Cho $\Delta ABC\,\,(AB < AC)$ nội tiếp đường tròn $\left( O \right)$ có BC là đường kính, vẽ đường cao AH của $\Delta ABC$ . $(H \in BC)$

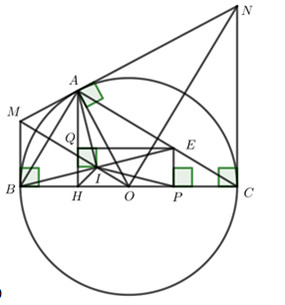
a) Biết $AB = 6cm,\,\,AC = 8cm$ . Tính độ dài AH và HB .

$\Delta ABC\,$ nội tiếp đường tròn $\left( O \right)$ có BC là đường kính

$\Rightarrow \angle BAC = {90^o}$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow \Delta ABC$ vuông tại A

Áp dụng định lý Py-ta-go vào $\Delta ABC$ vuông tại A ta được:

$BC = \sqrt {A{B^2} + A{C^2}}  = \sqrt {{6^2} + {8^2}}  = \sqrt {100}  = 10\,\,(cm)$

Áp dụng hệ thức lượng trong tam giác ABC vuông tại A ,

đường cao AH ta được:

$A{B^2} = HB.BC \Rightarrow HB = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{6^2}}}{{10}} = 3,6\,\,(cm)$

Áp dụng định lý Py-ta-go vào $\Delta ABH$ vuông tại H ta được:

$AH = \sqrt {A{B^2} - A{C^2}}  = \sqrt {{6^2} - 3,{6^2}}  = \sqrt {23,04}  = 4,8\,\,(cm)$

b) Tiếp tuyến tại A của $\left( O \right)$ cắt các tiếp tuyến tại B và C lần lượt tại M và N . Chứng minh $MN = MB + NC$ và $\angle MON = {90^o}$

Ta có MA, MB là hai tiếp tuyến của $\left( O \right)$ cắt nhau tại M

$\Rightarrow$$MA = MB$ và OM là phân giác của $\angle AOB$ (tính chất hai tiếp tuyến cắt nhau)

Ta có NA, NC là hai tiếp tuyến của $\left( O \right)$ cắt nhau tại N

$\Rightarrow$$NA = NC$và ON là phân giác của $\angle AOC$ (tính chất hai tiếp tuyến cắt nhau)

Mà $MN = MA + NA\,\,\,(A \in MN)$nên $MN = MB + NC\;\;\left( {dpcm} \right)$

OM, ON lần lượt là phân giác $\angle AOB$ và $\angle AOC$ (cmt)

Mà $\angle AOB$ và $\angle AOC$ là 2 góc kề bù nên $\angle MON = {90^o}.$

c) Trên cạnh AC lấy điểm E sao cho $AB = AE$ , gọi I là trung điểm của BE . Chứng minh 3 điểm M, I, O thẳng hàng.

Có I là trung điểm của BE $\Rightarrow$ AI là trung tuyến ứng với cạnh huyền trong tam giác $\Delta ABE$ vuông tại A

$\Rightarrow$$IA = IB = IE = \dfrac{1}{2}BE$ (tính chất đường trung tuyến trong tam giác vuông)

Ta có $MA = MB$ (cmt) $\Rightarrow$ M thuộc đường trung trực của AB (1)

$OA = OB\,\,( = R)$$\Rightarrow$ O thuộc đường trung trực của AB (2)

$IA = IB$ (cmt) $\Rightarrow$ I thuộc đường trung trực của AB (3)

Từ (1), (2), (3) $\Rightarrow$ 3 điểm M, I, O thẳng hàng.

d) Chứng minh HI là tia phân giác của $\angle AHC$

Từ E kẻ $EP \bot BC$ tại P và $EQ \bot AH$ tại Q .

$\Rightarrow HPEQ$ là hình chữ nhật $\Rightarrow$$QE = HP$

Ta có $\angle ABC + \angle ACB = {90^o}$ ($\Delta ABC$ vuông tại A )

$\angle HAC + \angle ACB = {90^o}$($\Delta AHC$ vuông tại H )

$\Rightarrow \angle ABC = \angle HAC$hay $\angle ABH = \angle QAE$

Xét $\Delta BHA$ và$\Delta AQE$có:$\angle BHA = \angle AQE\,\,( = {90^o})$; $\angle ABH = \angle QAE$ (cmt); $AB = AE$ (gt)

$\Rightarrow \Delta BHA = \Delta AQE$ (ch-gn)$\Rightarrow AH = QE = HP$

Ta có $\Delta BPE$ vuông tại P , I là trung điểm của BE

$\Rightarrow$$PI = \dfrac{1}{2}BE$(tính chất đường trung tuyến trong tam giác vuông)

Mà $AI = \dfrac{1}{2}BE$(cmt) $\Rightarrow AI = PI$

Xét $\Delta AHI$ và $\Delta PHI$ có: HI chung; $AI = PI$ (cmt); $AH = HP$ (cmt)

$\Rightarrow \Delta AHI = \Delta PHI$ (c-c-c) $\Rightarrow \angle AHI = \angle PHI$ (2 góc tương ứng)

$\Rightarrow$ HI là tia phân giác của $\angle AHC\;\;\left( {dpcm} \right).$

Câu 5:

Với sự phát triển của khoa học kỹ thuật hiện nay, người ta tạo ra nhiều mẫu xe lăn đẹp và tiện dụng cho người khuyết tật. Công ty A đã sản xuất ra những chiếc xe lăn cho người khuyết tật với số vốn ban đầu là 500 triệu đồng ( dùng để mua nguyên vật liệu và thiết bị sản xuất ). Chi phí để sản xuất ra một chiếc xe lăn là 2,5 triệu đồng. Giá bán ra thị trường mỗi chiếc là 3 triệu đồng.

a) Em hãy viết hàm số biểu diễn tổng số tiền đã đầu tư đến khi sản xuất ra được x chiếc xe lăn ( gồm vốn ban đầu và chi phí sản xuất ) và hàm số biểu diễn số tiền thu được khi bán ra x chiếc xe lăn.

Đơn vị tính là triệu đồng.

Hàm số biểu diễn tổng số tiền đã đầu tư đến khi sản xuất ra được x chiếc xe lăn là:

$y = 2,5x + 500\,\,\,\,\,\,(1)$

Hàm số biểu diễn số tiền thu được khi bán ra x chiếc xe lăn là:  $y = 3x\,\,\,(2)$

b) Công ty A phải bán bao nhiêu chiếc xe lăn với giá trên mới có thể thu hồi được đủ số tiền vốn đã đầu tư ban đầu? ( Gồm vốn ban đầu và chi phí sản xuất )

Gọi $x\;\;\left( {x \in {N^*}} \right)$ là số chiếc xe lăn bán ra đủ để thu lại vốn.

Để thu được số vốn ban đầu thì số tiền vốn ban đầu phải bằng số tiền thu được.

$\begin{array}{l} \Rightarrow 2,5\;x + 500 = 3x \Leftrightarrow x = 1000\;\;\left( {tm} \right).\\ \Rightarrow y = 3.1000 = 3000.\end{array}$

Vậy bán 1000 chiếc thu hồi đủ vốn đầu tư ban đầu là 3 tỉ đồng