Đề số 26 - Đề thi vào lớp 10 môn Toán — Không quảng cáo

Đề bài

Câu 1. (1,5 điểm)

1)  Tìm \(x\) , biết \(2\sqrt x  = 3.\)

2) Giải phương trình: \(43{x^2} - 2018x + 1975 = 0.\)

3)      Cho hàm số \(y = \left( {a + 1} \right){x^2}.\) Tìm a để hàm số nghịch biến khi \(x < 0\)  và đồng biến khi \(x > 0.\)

Câu 2. (2,0 điểm) Cho phương trình: \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 2 = 0\,\,\left( 1 \right),\) m là tham số

1) Tìm m để \(x = 2\) là nghiệm của phương trình (1).

2)  Xác định m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn điều kiện: \(x_1^2 + x_2^2 = 10\)

Câu 3. (1,5 điểm):

1) Trong mặt phẳng tọa độ \(Oxy\) cho các đường thẳng có phương trình: \(\left( {{d_1}} \right):\;\;y = x + 2,\;\;\left( {{d_2}} \right):\;\;y =  - 2\)  và \(\;\left( {{d_3}} \right):\;\;y = \left( {k + 1} \right)x + k.\) Tìm \(k\) để các đường thẳng trên đồng quy.

2) Rút gọn và tìm giá trị lớn nhất của biểu thức:\(A = \left( {\dfrac{1}{{1 - \sqrt x }} + \dfrac{{x + 2}}{{x\sqrt x  - 1}} + \dfrac{{\sqrt x }}{{x + \sqrt x  + 1}}} \right):\dfrac{{\sqrt x  - 1}}{3}\) (với \(x \ge 0,x \ne 1\)).

Câu 4. (3 điểm):

Cho tam giác \(ABC\) có ba góc nhọn và \(\widehat {A\;} = {45^0}.\)  Gọi \(D,\;E\)  lần lượt là hình chiếu vuông góc của \(B,\;C\) lên \(AC,\;AB;\;H\) là giao điểm của \(BD\) và \(CE.\)

1) Chứng minh tứ giác \(BEDC\) nội tiếp.

2) Chứng minh \(DE.AB = BC.AD\) và tính tỉ số \(\dfrac{{ED}}{{BC}}.\)

3) Chứng minh \(HE + HD = BE + CD.\)

4) Gọi \(I\) là tâm đường tròn ngoại tiếp tam giác \(ABC.\) Chứng minh \(AI \bot DE.\)

Câu 5. (1 điểm):

Cho \(n\) là số tự nhiên khác \(0.\) Tìm giá trị nhỏ nhất của:

\(Q = \sqrt {1 + \dfrac{1}{{{1^2}}} + \dfrac{1}{{{2^2}}}}  + \sqrt {1 + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}}}  \)\(\,+ \sqrt {1 + \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}}}  + .....\)\(\, + \sqrt {1 + \dfrac{1}{{{n^2}}} + \dfrac{1}{{{{\left( {n + 1} \right)}^2}}}}  + \dfrac{{101}}{{n + 1}}.\)

Lời giải chi tiết

Câu 1.

1) Tìm \(x\) , biết \(2\sqrt x  = 3.\)

Điều kiện: \(x \ge 0\)

\(2\sqrt x  = 3 \Leftrightarrow \sqrt x  = \dfrac{3}{2} \Leftrightarrow x = \dfrac{9}{4}\left( {tm} \right)\)

Vậy \(x = \dfrac{9}{4}\) .

2) Giải phương trình: \(43{x^2} - 2018x + 1975 = 0.\)

Ta có: \(a + b + c = 43 - 2018 + 1975 = 0\) . Nên phương trình luôn có 1 nghiệm là\(x = 1\) và nghiệm còn lại là \(x = \dfrac{c}{a} = \dfrac{{1975}}{{43}}\)

Vậy tập nghiệm của phương trình là: \(S = \left\{ {1;\dfrac{{1975}}{{43}}} \right\}\)

3) Cho hàm số \(y = \left( {a + 1} \right){x^2}.\) Tìm a để hàm số nghịch biến khi \(x < 0\)  và đồng biến khi \(x > 0.\)

+) Hàm số nghịch biến khi \(x < 0\) là: \(a + 1 > 0 \Leftrightarrow a >  - 1\)

+) Hàm số đồng biến khi \(x > 0.\) là: \(a + 1 > 0 \Leftrightarrow a >  - 1\)

Vậy với \(a >  - 1\) thì hàm số nghịch biến khi \(x < 0\)  và đồng biến khi \(x > 0.\)

Câu 2.

\({x^2} - 2\left( {m + 1} \right)x + {m^2} + 2 = 0\,\,\left( 1 \right),\)

1) Tìm m để \(x = 2\) là nghiệm của phương trình (1).

Thay \(x = 2\) vào phương trình  (1) ta có: \({2^2} - 2\left( {m + 1} \right).2 + {m^2} + 2 = 0\,\, \)

\(\Leftrightarrow {m^2} - 4m + 2 = 0\)

\(\Leftrightarrow \left[ \begin{array}{l}m = 2 - \sqrt 2 \\m = 2 + \sqrt 2 \end{array} \right.\)

Vậy với \(x = 2\) thì \(m \in \left\{ {2 - \sqrt 2 ;2 + \sqrt 2 } \right\}\)

2) Xác định m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn điều kiện: \(x_1^2 + x_2^2 = 10\)

Phương trình có hai nghiệm phân biệt \({x_1},{x_2}\) khi và chỉ khi: \(\Delta ' > 0 \Leftrightarrow {\left( {m + 1} \right)^2} - {m^2} - 2 > 0\)

\(\Leftrightarrow {m^2} + 2m + 1 - {m^2} - 2 > 0\)

\(\Leftrightarrow m > \dfrac{1}{2}\)

Theo hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right)\\{x_1}{x_2} = {m^2} + 2\end{array} \right.\)

Theo đề bài ta có:

\(\begin{array}{l}\;\;\;\;x_1^2 + x_2^2 = 10 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 10\\ \Leftrightarrow 4{\left( {m + 1} \right)^2} - 2\left( {{m^2} + 2} \right) = 10\\ \Leftrightarrow 2\left( {{m^2} + 2m + 1} \right) - {m^2} - 2 = 5\\ \Leftrightarrow 2{m^2} + 4m + 2 - {m^2} - 2 - 5 = 0\\ \Leftrightarrow {m^2} + 4m - 5 = 0\\ \Leftrightarrow {m^2} + 5m - m - 5 = 0\\ \Leftrightarrow \left( {m - 1} \right)\left( {m + 5} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\left( {tm} \right)\\m =  - 5\left( {ktm} \right)\end{array} \right.\end{array}\)

Vậy m = 1 thỏa mãn yêu cầu bài toán.

Câu 3:

1) Trong mặt phẳng tọa độ \(Oxy\) cho các đường thẳng có phương trình: \(\left( {{d_1}} \right):\;\;y = x + 2,\;\;\left( {{d_2}} \right):\;\;y =  - 2\)  và \(\;\left( {{d_3}} \right):\;\;y = \left( {k + 1} \right)x + k.\) Tìm \(k\) để các đường thẳng trên đồng quy.

Tọa độ giao điểm của đường thẳng \({d_1}\) và \({d_2}\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}y = x + 2\\y =  - 2\end{array} \right.\)

\(\Leftrightarrow \left\{ \begin{array}{l}x =  - 4\\y =  - 2\end{array} \right. \Rightarrow A\left( { - 4;\; - 2} \right).\)

\( \Rightarrow \) Ba đường thẳng đã cho đồng quy khi đường thẳng \({d_3}\) phải đi qua điểm \(A\left( { - 4; - 2} \right) \Rightarrow  - 2 = \left( {k + 1} \right)\left( { - 4} \right) + k\)

\( \Leftrightarrow  - 2 =  - 4k - 4 + k \)

\(\Leftrightarrow 3k =  - 2 \Leftrightarrow k =  - \dfrac{2}{3}.\)

Vậy \(k =  - \dfrac{2}{3}.\)

2) Rút gọn và tìm giá trị lớn nhất của biểu thức:\(A = \left( {\dfrac{1}{{1 - \sqrt x }} + \dfrac{{x + 2}}{{x\sqrt x  - 1}} + \dfrac{{\sqrt x }}{{x + \sqrt x  + 1}}} \right):\dfrac{{\sqrt x  - 1}}{3}\) (với \(x \ge 0,\;\;x \ne 1\)).

\(\begin{array}{l}A = \left( {\dfrac{1}{{1 - \sqrt x }} + \dfrac{{x + 2}}{{x\sqrt x  - 1}} + \dfrac{{\sqrt x }}{{x + \sqrt x  + 1}}} \right):\dfrac{{\sqrt x  - 1}}{3}\\\;\;\; = \left( {\dfrac{{ - 1}}{{\sqrt x  - 1}} + \dfrac{{x + 2}}{{\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}} + \dfrac{{\sqrt x }}{{x + \sqrt x  + 1}}} \right).\dfrac{3}{{\sqrt x  - 1}}\\\;\;\; = \dfrac{{ - \left( {x + \sqrt x  + 1} \right) + x + 2 + \sqrt x \left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}}.\dfrac{3}{{\sqrt x  - 1}}\\\;\;\; = \dfrac{{ - x - \sqrt x  - 1 + x + 2 + x - \sqrt x }}{{\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}}.\dfrac{3}{{\sqrt x  - 1}}\\\;\; = \dfrac{{x - 2\sqrt x  + 1}}{{\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}}.\dfrac{3}{{\sqrt x  - 1}}\\\;\; = \dfrac{{{{\left( {\sqrt x  - 1} \right)}^2}}}{{\left( {\sqrt x  - 1} \right)\left( {x + \sqrt x  + 1} \right)}}.\dfrac{3}{{\sqrt x  - 1}} \\\;\;= \dfrac{3}{{x + \sqrt x  + 1}}.\end{array}\)

Ta có: \(A = \dfrac{3}{{x + \sqrt x  + 1}}\)

Ta có: \(x \ge 0,x \ne 1 \Rightarrow \sqrt x  \ge 0 \)

\(\Rightarrow x + \sqrt x  + 1 \ge 1 \)

\(\Rightarrow \dfrac{3}{{x + \sqrt x  + 1}} \le 3\)

Vậy giá trị lớn nhất của biểu thức A là 3. Dấu “=” xảy ra khi và chỉ khi: \(x = 0\)

Câu 4:

Cho tam giác \(ABC\) có ba góc nhọn và \(\widehat {A\;} = {45^0}.\)  Gọi \(D,\;E\)  lần lượt là hình chiếu vuông góc của \(B,\;C\) lên \(AC,\;AB;\;H\) là giao điểm của \(BD\) và \(CE.\)

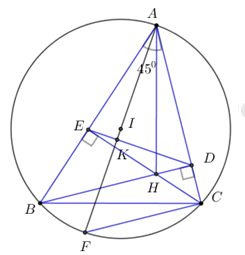
1) Chứng minh tứ giác \(BEDC\) nội tiếp.

Xét tứ giác \(BEDC\) ta có: \(\widehat {BDC} = \widehat {BEC} = {90^0}\left( {gt} \right)\)

Mà hai đỉnh kề nhau D và E cùng nhìn cạnh \(BC\) dưới hai góc bằng nhau.

\( \Rightarrow BEDC\) là tứ giác nội tiếp. (dấu hiện nhận biết tứ giác nội tiếp).

2) Chứng minh \(DE.AB = BC.AD\) và tính tỉ số \(\dfrac{{ED}}{{BC}}.\)

Vì \(BEDC\) là tứ giác nội tiếp (cmt) \( \Rightarrow \widehat {ADE} = \widehat {ABC}\) (góc trong tại một đỉnh bằng góc ngoài tại đỉnh đối diện).

Xét \(\Delta ADE\) và \(\Delta ABC\) ta có:

\(\begin{array}{l}\widehat {A\;}\;\;chung\\\widehat {ABC} = \widehat {ADE}\;\;\left( {cmt} \right)\\ \Rightarrow \Delta ADE \sim \Delta ABC\;\;\left( {g - g} \right).\\ \Rightarrow \dfrac{{AD}}{{AB}} = \dfrac{{ED}}{{BC}} \\\Rightarrow AD.BC = AB.DE\;\;\left( {dpcm} \right).\end{array}\)

Xét \(\Delta ADB\) vuông tại \(D\) có \(\widehat {BAD} = {45^0} \Rightarrow \Delta ADB\) vuông cân tại \(D \Rightarrow AD = BD \)

\(\Rightarrow AB = AD\sqrt 2 .\)

\( \Rightarrow \dfrac{{AD}}{{AB}} = \dfrac{{ED}}{{BC}} = \dfrac{{AD}}{{AD\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}.\)

Vậy \(\dfrac{{ED}}{{BC}} = \dfrac{{\sqrt 2 }}{2}.\)

3) Chứng minh \(HE + HD = BE + CD.\)

Ta có \(\Delta ADB\) vuông cân tại \(D \Rightarrow \widehat {ABD} = \widehat {BAD} = {45^0}.\)

\( \Rightarrow \Delta BEH\) vuông cân tại \(E\;\;\left( {do\;\;\widehat {BEH} = {{90}^0},\;\;\widehat {EBH} = {{45}^0}} \right) \)

\(\Rightarrow EH = BE\) (tính chất tam giác cân).

\(\Delta AEC\) vuông cân tại \(E\;\;\left( {do\;\;\widehat {EAC} = {{45}^0}} \right)\)

\(\Rightarrow \widehat {ACD} = {45^0}.\)

\( \Rightarrow \Delta HDC\) vuông cân tại \(H\;\left( {do\;\;\widehat {HDC} = {{90}^0},\;\;\widehat {DCH} = {{45}^0}} \right)\)

\(\Rightarrow HD = DC.\) (tính chất tam giác cân).

\( \Rightarrow BE + CD = HE + HD\;\;\left( {dpcm} \right).\)

4) Gọi \(I\) là tâm đường tròn ngoại tiếp tam giác \(ABC.\) Chứng minh \(AI \bot DE.\)

Kéo dài \(AI\) cắt đường tròn tại điểm thứ hai là \(F.\)

Giả sử \(AI \cap DE = \left\{ K \right\}.\)

Khi đó ta có: \(\widehat {ACF}\) là góc nội tiếp chắn nửa đường tròn \( \Rightarrow \widehat {ACF} = {90^0}.\)

Ta có: \(\widehat {ABD} = \widehat {AFC}\) (hai góc nội tiếp cùng chắn cung \(AC\))

Mà \(\widehat {ABC} = \widehat {ADE}\;\;\left( {cmt} \right)\)

\(\Rightarrow \widehat {ADE} = \widehat {AFC}\;\;\left( { = \widehat {ADE}} \right).\)

Xét tứ giác \(DKFC\) ta có: \(\widehat {ADK} = \widehat {KFC}\;\;\left( {cmt} \right).\)

\( \Rightarrow DKFC\) là tứ giác nội tiếp (góc trong tại một đỉnh bằng góc ngoài tại đỉnh đối diện).

\( \Rightarrow \widehat {DCF} + \widehat {DKF} = {180^0}\)

\(\Leftrightarrow \widehat {DKF} = {180^0} - \widehat {DCF} = {90^0}\)  (tổng hai góc đối diện trong tứ giác nội tiếp)

Hay \(AI \bot DE\;\;\left( {dpcm} \right).\)