Đề số 30 - Đề thi vào lớp 10 môn Toán
Đề thi vào lớp 10 môn Toán - Đề số 30 có đáp án và lời giải chi tiết
Đề bài
Câu 1 (1 điểm):
Thực hiện phép tính: \(\left( {\sqrt 3 + 1} \right).\dfrac{{\sqrt 3 - 3}}{{2\sqrt 3 }}.\)
Câu 2 (1 điểm):
Cho hàm số \(y = - \dfrac{1}{2}{x^2}\) có đồ thị \(\left( P \right)\) và đường thẳng \(\left( d \right):\;\;y = 3 - 4x.\) Lập phương trình đường thẳng \(\left( \Delta \right)\) song song với \(\left( d \right)\) và cắt \(\left( P \right)\) tại điểm \(M\) có hoành độ bằng \(2.\)
Câu 3 (1 điểm):
Rút gọn biểu thức sau: \(A = \left( {1 - \dfrac{{2\sqrt x }}{{3\sqrt x + 1}} - \dfrac{{1 - 2\sqrt x }}{{1 - 9x}}} \right):\left( {\dfrac{{6\sqrt x + 5}}{{3\sqrt x + 1}} - 2} \right)\)\(\;\;\;\left( {x \ge 0,\;\;x \ne \dfrac{1}{9}} \right).\)
Câu 4 (1,5 điểm):
Cho phương trình \({x^2} - x + m + 1 = 0\) ( m là tham số).
a) Giải phương trình với \(m = - 3.\)
b) Tìm tất cả các giá trị của m để phương trình đã cho có hai nghiệm \({x_1},\;{x_2}\) thỏa mãn điều kiện: \(\left| {{x_1} - {x_2}} \right| = 2.\)
Câu 5 (1 điểm):
Một tam giác vuông có chu vi bằng 24 cm. Độ dài hai cạnh góc vuông hơn kém nhau 2 cm. Tính diện tích tam giác vuông đó.
Câu 6 (1,0 điểm) Cho hình nón có bán kính đáy bằng 3m, diện tích toàn phần bằng \(24\pi \,\,{m^2}\). Tính thể tích của hình nón.
Câu 7 (2,5 điểm) Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao AA’, BB’, CC’ của tam giác ABC cắt nhau tại H. Đường thẳng AO cắt đường tròn tâm O tại D khác A.
a) Chứng minh tứ giác AB’HC’ nội tiếp đường tròn.
b) Gọi I là giao điểm của hai đường thẳng HD và BC. Chứng minh I là trung điểm của đoạn BC.
c) Tính \(\dfrac{{AH}}{{AA'}} + \dfrac{{BH}}{{BB'}} + \dfrac{{CH}}{{CC'}}\).
Câu 8 (1,0 điểm) Tìm giá trị nhỏ nhất của biểu thức \(T = 3{x^2} + 4{y^2} + 4xy + 2x - 4y + 2021\)
Lời giải chi tiết
Câu 1:
Thực hiện phép tính: \(\left( {\sqrt 3 + 1} \right).\dfrac{{\sqrt 3 - 3}}{{2\sqrt 3 }}.\)
\(\begin{array}{l}\;\;\;\left( {\sqrt 3 + 1} \right).\dfrac{{\sqrt 3 - 3}}{{2\sqrt 3 }}\\ = \left( {\sqrt 3 + 1} \right)\dfrac{{\sqrt 3 \left( {1 - \sqrt 3 } \right)}}{{2\sqrt 3 }}\\ = \dfrac{{\sqrt 3 \left( {1 - 3} \right)}}{{2\sqrt 3 }} = \dfrac{{ - 2\sqrt 3 }}{{2\sqrt 3 }} = - 1.\end{array}\)
Câu 2:
Cho hàm số \(y = - \dfrac{1}{2}{x^2}\) có đồ thị \(\left( P \right)\) và đường thẳng \(\left( d \right):\;\;y = 3 - 4x.\) Lập phương trình đường thẳng \(\left( \Delta \right)\) song song với \(\left( d \right)\) và cắt \(\left( P \right)\) tại điểm \(M\) có hoành độ bằng \(2.\)
Gọi phương trình đường thẳng \(\left( \Delta \right):\;\;y = ax + b.\)
Khi đó \(\left( \Delta \right)//\left( d \right) \Rightarrow \left\{ \begin{array}{l}a = - 4\\b \ne 3\end{array} \right.\) \( \Rightarrow \left( \Delta \right):\;\;y = - 4x + b.\)
Điểm \(M\) có hoành độ bằng \(2\) và thuộc đồ thị hàm số \(\left( P \right) \Rightarrow y = - \dfrac{1}{2}{.2^2} = - 2 \Rightarrow M\left( {2; - 2} \right).\)
Điểm \(M\left( {2; - 2} \right) \in \left( \Delta \right) \) \(\Rightarrow - 2 = - 4.2 + b \Leftrightarrow b = 6\;\;\left( {tm} \right).\)
Vậy phương trình đường thẳng \(\left( \Delta \right):\;\;y = - 4x + 6.\)
Câu 3:
Rút gọn biểu thức sau: \(A = \left( {1 - \dfrac{{2\sqrt x }}{{3\sqrt x + 1}} - \dfrac{{1 - 2\sqrt x }}{{1 - 9x}}} \right):\left( {\dfrac{{6\sqrt x + 5}}{{3\sqrt x + 1}} - 2} \right)\;\;\;\left( {x \ge 0,\;\;x \ne \dfrac{1}{9}} \right).\)
\(\begin{array}{l}A = \left( {1 - \dfrac{{2\sqrt x }}{{3\sqrt x + 1}} - \dfrac{{1 - 2\sqrt x }}{{1 - 9x}}} \right):\left( {\dfrac{{6\sqrt x + 5}}{{3\sqrt x + 1}} - 2} \right)\;\;\;\left( {x \ge 0,\;\;x \ne \dfrac{1}{9}} \right)\\\;\;\; = \left( {1 - \dfrac{{2\sqrt x }}{{3\sqrt x + 1}} + \dfrac{{1 - 2\sqrt x }}{{\left( {3\sqrt x + 1} \right)\left( {3\sqrt x - 1} \right)}}} \right):\left( {\dfrac{{6\sqrt x + 5 - 2\left( {3\sqrt x + 1} \right)}}{{3\sqrt x + 1}}} \right)\\\;\;\; = \dfrac{{9x - 1 - 2\sqrt x \left( {3\sqrt x - 1} \right) + 1 - 2\sqrt x }}{{\left( {3\sqrt x + 1} \right)\left( {3\sqrt x - 1} \right)}}:\dfrac{{6\sqrt x + 5 - 6\sqrt x - 2}}{{3\sqrt x + 1}}\\\;\;\; = \dfrac{{9x - 1 - 6x + 2\sqrt x + 1 - 2\sqrt x }}{{\left( {3\sqrt x + 1} \right)\left( {3\sqrt x - 1} \right)}}.\dfrac{{3\sqrt x + 1}}{3}\\\;\;\; = \dfrac{{3x}}{{3\left( {3\sqrt x - 1} \right)}} = \dfrac{x}{{3\sqrt x - 1}}.\end{array}\)
Câu 4:
Cho phương trình \({x^2} - x + m + 1 = 0\) ( m là tham số).
a) Giải phương trình với \(m = - 3.\)
Với \(m = - 3\) ta có phương trình: \({x^2} - x - 2 = 0\)
Ta có: \(a = 1;\;b = - 1;\;c = - 2\) \( \Rightarrow a - b + c = 1 + 1 - 2 = 0.\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \({x_1} = - 1;\;\;{x_2} = - \dfrac{c}{a} = 2.\)
Vậy với \(m = - 3\) phương trình có tập nghiệm \(S = \left\{ { - 1;\;2} \right\}.\)
b) Tìm tất cả các giá trị của m để phương trình đã cho có hai nghiệm \({x_1},\;{x_2}\) thỏa mãn điều kiện: \(\left| {{x_1} - {x_2}} \right| = 2.\)
Phương trình có hai nghiệm \( \Leftrightarrow \Delta \ge 0\) \( \Leftrightarrow 1 - 4\left( {m + 1} \right) \ge 0 \Leftrightarrow m \le - \dfrac{3}{4}.\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 1\\{x_1}{x_2} = m + 1\end{array} \right..\)
Theo đề bài ta có: \(\left| {{x_1} - {x_2}} \right| = 2\)
\(\begin{array}{l} \Leftrightarrow {\left| {{x_1} - {x_2}} \right|^2} = 4\\ \Leftrightarrow x_1^2 - 2{x_1}{x_2} + x_2^2 = 4\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 4\\ \Leftrightarrow 1 - 4\left( {m + 1} \right) = 4\\ \Leftrightarrow 1 - 4m - 4 = 4\\ \Leftrightarrow m = - \dfrac{7}{4}\;\;\left( {tm} \right).\end{array}\)
Vậy \(m = - \dfrac{7}{4}\) thỏa mãn bài toán.
Câu 5:
Một tam giác vuông có chu vi bằng 24 cm. Độ dài hai cạnh góc vuông hơn kém nhau 2 cm. Tính diện tích tam giác vuông đó.
Gọi độ dài của cạnh góc vuông lớn của tam giác là \(x\;cm,\;\;\left( {2 < x \le 8} \right).\)
Khi đó độ dài cạnh góc vuông còn lại của tam giác là: \(x - 2\;\;\left( {cm} \right).\)
\( \Rightarrow \) Độ dài cạnh huyền của tam giác vuông là: \(24 - x - x + 2 = 26 - 2x\;\;\left( {cm} \right).\)
Áp dụng định lý Pi-ta-go cho tam giác vuông này ta có phương trình:
\(\begin{array}{l}\;\;\;\;{\left( {26 - 2x} \right)^2} = {x^2} + {\left( {x - 2} \right)^2}\\ \Leftrightarrow 676 - 104x + 4{x^2} = 2{x^2} - 4x + 4\\ \Leftrightarrow 2{x^2} - 100x + 672 = 0\\ \Leftrightarrow 2\left( {x - 42} \right)\left( {x - 8} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 42 = 0\\x - 8 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 42\;\;\left( {ktm} \right)\\x = 8\;\;\left( {tm} \right)\end{array} \right..\end{array}\)
\( \Rightarrow \) Độ dài cạnh góc vuông còn lại của tam giác là: \(8 - 2 = 6\left( {cm} \right).\)
Vậy diện tích của tam giác vuông là: \(S = \dfrac{1}{2}.8.6 = 24\;c{m^2}.\)
Câu 6.
\(\begin{array}{l}{S_{tp}} = 24\pi \,\,{m^2} \Rightarrow \pi r\left( {r + l} \right) = 24\pi \\ \Leftrightarrow 3\left( {3 + l} \right) = 24 \Leftrightarrow l = 5\,\,\left( m \right)\end{array}\)
\( \Rightarrow \) Độ dài đường sinh của hình nón bằng 5 m .
\( \Rightarrow \) Độ dài đường cao của hình nón là \(h = \sqrt {{l^2} - {r^2}} = \sqrt {{5^2} - {3^2}} = 4\,\,\left( m \right)\).
Vậy thể tích của khối nón là \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.3^2}.4 = 12\pi \,\,\left( {{m^3}} \right)\).
Câu 7.
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao AA’, BB’, CC’ của tam giác ABC cắt nhau tại H. Đường thẳng AO cắt đường tròn tâm O tại D khác A.
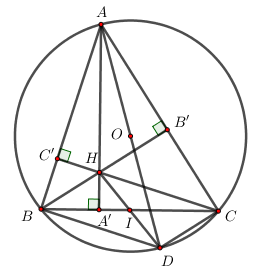
a) Chứng minh tứ giác AB’HC’ nội tiếp đường tròn.
Xét tứ giác AB’HC’ có \(\angle AB'H + \angle AC'H = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác AB’HC’ là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 180 0 ).
b) Gọi I là giao điểm của hai đường thẳng HD và BC. Chứng minh I là trung điểm của đoạn BC.
Ta có \(\angle ABD = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AB \bot BD\).
Mà \(CH \bot AB\,\,\left( {gt} \right) \Rightarrow BD\parallel CH\)
Chứng minh tương tự ta có \(CD\parallel BH\).
\( \Rightarrow \) Tứ giác BHCD là tứ giác nội tiếp (Tứ giác có các cặp cạnh đối song song)
Mà \(BC \cap HD = I\,\,\left( {gt} \right) \Rightarrow I\) là trung điểm của BC.
c) Tính \(\dfrac{{AH}}{{AA'}} + \dfrac{{BH}}{{BB'}} + \dfrac{{CH}}{{CC'}}\).
Ta có:
\(\dfrac{{{S_{HBC}}}}{{{S_{ABC}}}} = \dfrac{{\dfrac{1}{2}HA'.BC}}{{\dfrac{1}{2}AA'.BC}} = \dfrac{{HA'}}{{AA'}} \)
\(\Rightarrow 1 - \dfrac{{{S_{HBC}}}}{{{S_{ABC}}}} = 1 - \dfrac{{HA'}}{{AA'}} = \dfrac{{AA' - HA'}}{{AA'}} = \dfrac{{AH}}{{AA'}}\)
Chứng minh tương tự ta có: \(\dfrac{{BH}}{{BB'}} = 1 - \dfrac{{{S_{HAC}}}}{{{S_{ABC}}}};\,\,\dfrac{{CH}}{{CC'}} = 1 - \dfrac{{{S_{HAB}}}}{{{S_{ABC}}}}\)
\( \Rightarrow \dfrac{{AH}}{{AA'}} + \dfrac{{BH}}{{BB'}} + \dfrac{{CH}}{{CC'}} \)\(\;= 1 - \dfrac{{{S_{HBC}}}}{{{S_{ABC}}}} + 1 - \dfrac{{{S_{HAC}}}}{{{S_{ABC}}}} + 1 - \dfrac{{{S_{HAB}}}}{{{S_{ABC}}}} \)\(\;= 3 - \dfrac{{{S_{HBC}} + {S_{HAC}} + {S_{HAB}}}}{{{S_{ABC}}}} \)\(\;= 3 - 1 = 2\)
Câu 8.
\(\begin{array}{l}T = 3{x^2} + 4{y^2} + 4xy + 2x - 4y + 2021\\\;\;\; = \left( {{x^2} + 2x + 1} \right) + 2\left( {{y^2} - 2y + 1} \right) + 2\left( {{x^2} + {y^2} + 2xy} \right) + 2018\\\;\;\; = {\left( {x + 1} \right)^2} + 2{\left( {y - 1} \right)^2} + 2{\left( {x + y} \right)^2} + 2018 \ge 2018\\\left( {Do\,\,{{\left( {x + 1} \right)}^2} \ge 0;\,\,{{\left( {y - 1} \right)}^2} \ge 0;\,\,{{\left( {x + y} \right)}^2} \ge 0} \right)\end{array}\)
Dấu bằng xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x + 1 = 0\\y - 1 = 0\\x + y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 1\end{array} \right.\).
Vậy \({T_{\min }} = 2018 \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 1\end{array} \right.\).