Đề thi giữa kì 1 Toán 7 - Đề số 13
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Đề bài
Khẳng định nào sau đây đúng ?
-
A.
\(5 \in \mathbb{Q}\).
-
B.
\(\frac{{ - 3}}{2} \in \mathbb{Z}\).
-
C.
\( - 1,5 \in \mathbb{N}\).
-
D.
\(\frac{{ - 3}}{2} \notin \mathbb{Q}\).
Số đối của \(\frac{4}{7}\) là:
-
A.
\(\frac{7}{4}\).
-
B.
\(\frac{{ - 4}}{{ - 7}}\).
-
C.
\( - \frac{4}{7}\).
-
D.
\(\frac{{ - 7}}{4}\).
Trong các số \( - 4,5;\,\, - 2\frac{1}{3};\,\,\,\frac{{ - 4}}{{ - 5}};\,\,\,0;\,\,\,\frac{{ - 4}}{7};\,\,\,\frac{{24}}{{23}}\) có bao nhiêu số hữu tỉ âm?
-
A.
1.
-
B.
2.
-
C.
3.
-
D.
4.
-
A.
Điểm \(A\) biểu diễn số hữu tỉ \(\frac{{ - 3}}{2}\).
-
B.
Điểm \(B\) biểu diễn số hữu tỉ \(\frac{{ - 1}}{3}\).
-
C.
Điểm \(C\) biểu diễn số hữu tỉ \(\frac{1}{2}\).
-
D.
Điểm \(D\) biểu diễn số hữu tỉ \(\frac{4}{3}\).
Kết quả của phép tính \({\left( {\frac{{ - 1}}{2}} \right)^3}\) là:
-
A.
\(\frac{{ - 1}}{6}\).
-
B.
\( - \frac{1}{8}\).
-
C.
\(\frac{{ - 1}}{{ - 8}}\).
-
D.
\(\frac{1}{8}\).
Với \(a,b,c\) là ba số hữu tỉ bất kì, nếu \(a - b = c\) thì:
-
A.
\(a = b + c\).
-
B.
\(a = - b - c\).
-
C.
\(a = b - c\).
-
D.
\(a = - b + c\).
Các mặt của hình lập phương đều là:
-
A.
Hình vuông.
-
B.
Tam giác đều.
-
C.
Hình chữ nhật.
-
D.
Hình thoi.
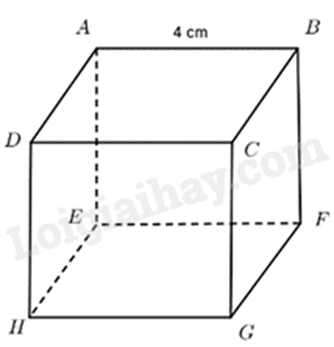
Cho hình lập phương ABCD . EFGH như hình vẽ, có cạnh bằng 4cm. Thể tích của hình lập phương đó là:
-
A.
\(64c{m^3}\).
-
B.
\(96c{m^3}\).
-
C.
\(16c{m^3}\).
-
D.
\(64c{m^2}\).
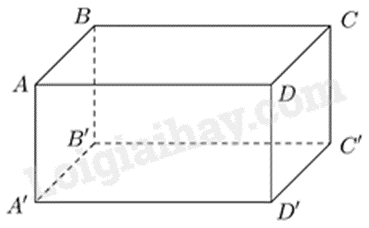
Hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 5\,{\rm{cm}}\); AA’ = 3cm. Khẳng định nào sau đây đúng?
-
A.
\(DC = 3\,{\rm{cm}}\).
-
B.
\(BB' = 5\,{\rm{cm}}\).
-
C.
\(D'C' = 5\,{\rm{cm}}\).
-
D.
\(A'D' = 5\,{\rm{cm}}\).
-
A.
3cm.
-
B.
4cm.
-
C.
5cm.
-
D.
7cm.
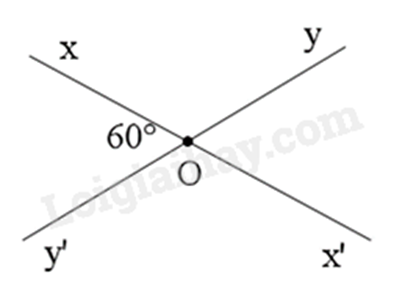
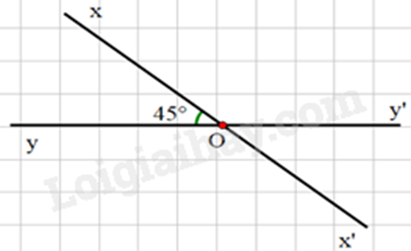
Cho đường thẳng xx’, yy’ cắt nhau tại O và \(\widehat {xOy} = 45^\circ \). Số đo \(\widehat {x'Oy'}\) bằng
-
A.
\(45^\circ \).
-
B.
\(90^\circ \).
-
C.
\(180^\circ \).
-
D.
\(135^\circ \).
-
A.
\(\widehat {y{\rm{AB}}}\).
-
B.
\(\widehat {y{\rm{A}}m}\).
-
C.
\(\widehat {m{\rm{AB}}}\).
-
D.
\(\widehat {x{\rm{A}}m}\).
Lời giải và đáp án
Khẳng định nào sau đây đúng ?
-
A.
\(5 \in \mathbb{Q}\).
-
B.
\(\frac{{ - 3}}{2} \in \mathbb{Z}\).
-
C.
\( - 1,5 \in \mathbb{N}\).
-
D.
\(\frac{{ - 3}}{2} \notin \mathbb{Q}\).
Đáp án : A
Dựa vào kiến thức về các tập hợp.
\(5 = \frac{5}{1}\) nên \(5 \in \mathbb{Q}\).
\(\frac{{ - 3}}{2} = - 1,5\) không phải số nguyên nên \(\frac{{ - 3}}{2} \notin \mathbb{Z}\).
\( - 1,5 < 0\) nên \( - 1,5 \notin \mathbb{N}\).
\(\frac{{ - 3}}{2}\) là số hữu tỉ nên \(\frac{{ - 3}}{2} \in \mathbb{Q}\).
Vậy khẳng định A đúng, khẳng định B, C, D sai.
Đáp án A.
Số đối của \(\frac{4}{7}\) là:
-
A.
\(\frac{7}{4}\).
-
B.
\(\frac{{ - 4}}{{ - 7}}\).
-
C.
\( - \frac{4}{7}\).
-
D.
\(\frac{{ - 7}}{4}\).
Đáp án : C
Số đối của số hữu tỉ a là – a.
Số đối của \(\frac{4}{7}\) là \( - \frac{4}{7}\).
Đáp án C.
Trong các số \( - 4,5;\,\, - 2\frac{1}{3};\,\,\,\frac{{ - 4}}{{ - 5}};\,\,\,0;\,\,\,\frac{{ - 4}}{7};\,\,\,\frac{{24}}{{23}}\) có bao nhiêu số hữu tỉ âm?
-
A.
1.
-
B.
2.
-
C.
3.
-
D.
4.
Đáp án : C
Số hữu tỉ âm là các số hữu tỉ nhỏ hơn 0.
Ta có: \( - 4,5 = - \frac{{45}}{{10}};\,\, - 2\frac{1}{3} = - \frac{7}{3};\,\,\,\frac{{ - 4}}{{ - 5}} = \frac{4}{5}\)
Vậy có 3 số hữu tỉ âm, đó là: \( - 4,5;\,\, - 2\frac{1}{3};\,\,\,\frac{{ - 4}}{7}.\)
Đáp án C.
-
A.
Điểm \(A\) biểu diễn số hữu tỉ \(\frac{{ - 3}}{2}\).
-
B.
Điểm \(B\) biểu diễn số hữu tỉ \(\frac{{ - 1}}{3}\).
-
C.
Điểm \(C\) biểu diễn số hữu tỉ \(\frac{1}{2}\).
-
D.
Điểm \(D\) biểu diễn số hữu tỉ \(\frac{4}{3}\).
Đáp án : A
Xác định 1 đơn vị của trục số, từ đó xác định số hữu tỉ tương ứng với các điểm.
Vì -1 cách 0 là 6 đơn vị nên 1 đơn vị tương ứng với: \(1:6 = \frac{1}{6}\).
Điểm A cách 0 là 7 đơn vị về phía bên trái nên điểm A biểu diễn số hữu tỉ \( - \frac{7}{6}\). (Khẳng định A sai).
Điểm B cách 0 là 2 đơn vị về phía bên trái nên điểm B biểu diễn số hữu tỉ \( - \frac{2}{6} = - \frac{1}{3}\). (Khẳng định B đúng).
Điểm C cách 0 là 3 đơn vị về bên phải nên điểm C biểu diễn số hữu tỉ \(\frac{3}{6} = \frac{1}{2}\). (Khẳng định C đúng).
Điểm D cách 0 là 8 đơn vị về bên phải nên điểm D biểu diễn số hữu tỉ \(\frac{8}{6} = \frac{4}{3}\). (Khẳng định D đúng).
Vậy chọn đáp án A.
Đáp án A.
Kết quả của phép tính \({\left( {\frac{{ - 1}}{2}} \right)^3}\) là:
-
A.
\(\frac{{ - 1}}{6}\).
-
B.
\( - \frac{1}{8}\).
-
C.
\(\frac{{ - 1}}{{ - 8}}\).
-
D.
\(\frac{1}{8}\).
Đáp án : B
Sử dụng kiến thức về lũy thừa \({\left( {\frac{a}{b}} \right)^n} = \frac{{{a^n}}}{{{b^n}}}\).
Ta có: \({\left( {\frac{{ - 1}}{2}} \right)^3} = \frac{{{{\left( { - 1} \right)}^3}}}{{{2^3}}} = - \frac{1}{8}\)
Đáp án B.
Với \(a,b,c\) là ba số hữu tỉ bất kì, nếu \(a - b = c\) thì:
-
A.
\(a = b + c\).
-
B.
\(a = - b - c\).
-
C.
\(a = b - c\).
-
D.
\(a = - b + c\).
Đáp án : A
Sử dụng quy tắc chuyển vế.
Nếu \(a - b = c\) thì \(a = b + c\).
Đáp án A.
Các mặt của hình lập phương đều là:
-
A.
Hình vuông.
-
B.
Tam giác đều.
-
C.
Hình chữ nhật.
-
D.
Hình thoi.
Đáp án : A
Dựa vào kiến thức về hình lập phương.
Hình lập phương có 6 mặt bằng nhau và đều là hình vuông.
Đáp án A.
Cho hình lập phương ABCD . EFGH như hình vẽ, có cạnh bằng 4cm. Thể tích của hình lập phương đó là:

-
A.
\(64c{m^3}\).
-
B.
\(96c{m^3}\).
-
C.
\(16c{m^3}\).
-
D.
\(64c{m^2}\).
Đáp án : A
Sử dụng công thức tính thể tích của hình lập phương: \(V = {a^3}\) (a là độ dài cạnh)
Thể tích của hình lập phương là: \(V = {4^3} = 64\left( {c{m^3}} \right)\).
Đáp án A.
Hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 5\,{\rm{cm}}\); AA’ = 3cm. Khẳng định nào sau đây đúng?

-
A.
\(DC = 3\,{\rm{cm}}\).
-
B.
\(BB' = 5\,{\rm{cm}}\).
-
C.
\(D'C' = 5\,{\rm{cm}}\).
-
D.
\(A'D' = 5\,{\rm{cm}}\).
Đáp án : C
Hình hộp chữ nhật có các cạnh đối bằng nhau.
Cạnh \(D'C' = DC = AB = 5cm\).
Cạnh \(BB' = AA' = 3cm\).
Cạnh \(A'D'\) chưa đủ điều kiện để xác định.
Vậy đáp án đúng là C.
Đáp án C.
-
A.
3cm.
-
B.
4cm.
-
C.
5cm.
-
D.
7cm.
Đáp án : C
Dựa vào kiến thức về hình lăng trụ đứng tam giác.
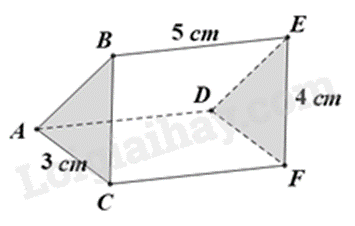
Hình lăng trụ có hai đáy là ABC, DEF, chiều cao là BE = 5cm.
Đáp án C.
Cho đường thẳng xx’, yy’ cắt nhau tại O và \(\widehat {xOy} = 45^\circ \). Số đo \(\widehat {x'Oy'}\) bằng

-
A.
\(45^\circ \).
-
B.
\(90^\circ \).
-
C.
\(180^\circ \).
-
D.
\(135^\circ \).
Đáp án : A
Dựa vào kiến thức về hai góc đối đỉnh.
Vì đường thẳng xx’, yy’ cắt nhau tại O nên \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) là hai góc đối đỉnh, suy ra \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \).
Đáp án A.
-
A.
\(\widehat {y{\rm{AB}}}\).
-
B.
\(\widehat {y{\rm{A}}m}\).
-
C.
\(\widehat {m{\rm{AB}}}\).
-
D.
\(\widehat {x{\rm{A}}m}\).
Đáp án : A
Hai góc kề bù là hai góc vừa kề, vừa bù nhau.
Góc kề bù với \(\widehat {xAB}\) là \(\widehat {yAB}\).
Đáp án A.
Sử dụng các quy tắc tính với số hữu tỉ và lũy thừa với số mũ tự nhiên.
a) \(\frac{4}{9} + \frac{5}{9}.\frac{{ - 3}}{{10}}\)
\(\begin{array}{l} = \frac{4}{9} + \frac{{ - 1}}{6}\\ = \frac{8}{{18}} + \frac{{ - 3}}{{18}}\\ = \frac{5}{{18}}\end{array}\)
b) \(\frac{9}{{25}}.\frac{{ - 23}}{{11}} + \frac{1}{{11}}.{\left( {\frac{3}{5}} \right)^2}\)
\( = \frac{9}{{25}}.\frac{{ - 23}}{{11}} + \frac{1}{{11}}.\frac{9}{{25}}\)
\( = \frac{9}{{25}}.\left( {\frac{{ - 23}}{{11}} + \frac{1}{{11}}} \right)\)
\( = \frac{9}{{25}}.( - 2)\)
\( = - \frac{{18}}{{25}}\)
c) \(\frac{{{8^3} + {4^4} - {2^7}}}{{{{25.2}^6}}}\)
\( = \frac{{{{\left( {{2^3}} \right)}^3} + {{\left( {{2^2}} \right)}^4} - {2^7}}}{{{5^2}{{.2}^6}}} = \frac{{{2^9} + {2^8} - {2^7}}}{{{5^2}{{.2}^6}}}\)
\( = \frac{{{2^7}.\left( {{2^2} + 2 - 1} \right)}}{{{5^2}{{.2}^6}}}\)
\(\begin{array}{l} = \frac{{{2^7}.5}}{{{5^2}{{.2}^6}}}\\ = \frac{2}{5}\end{array}\)
Sử dụng quy tắc chuyển vế.
a) \(x - \frac{3}{2} = - \frac{4}{5}\)
\(\begin{array}{l}x\, = - \frac{4}{5} + \frac{3}{2}\\x = - \frac{8}{{10}} + \frac{{15}}{{10}}\\x\, = \frac{7}{{10}}\end{array}\)
Vậy \(x = \frac{7}{{10}}\).
b) \(\frac{5}{7}x + \frac{5}{8} = - 0,375\)
\(\begin{array}{l}\frac{5}{7}x + \frac{5}{8} = - \frac{3}{8}\\\frac{5}{7}x = - \frac{3}{8} - \frac{5}{8}\\\frac{5}{7}x\, = - 1\\x = - 1:\frac{5}{7}\\x\,\, = - \frac{7}{5}\end{array}\)
Vậy \(x\,\, = - \frac{7}{5}\).
Sử dụng kiến thức về hai góc đối đỉnh và hai góc kề bù.
Vì xx’ cắt yy’ tại O nên \(\widehat {yOx'} = \widehat {xOy'} = 60^\circ \) (hai góc đối đỉnh).
Vì \(\widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {xOy'} = 180^\circ \)
suy ra \(\widehat {xOy} = 180^\circ - \widehat {xOy'} = 180^\circ - 60^\circ = 120^\circ \).
Sử dụng công thức tính diện tích xung quanh và thể tích hình lăng trụ:
S xq = C đáy .chiều cao.
V = S đáy .chiều cao.
Tính diện tích xung quanh của hình lăng trụ ABC.DEF là:
\({S_{xq}} = \left( {6 + 9 + 8} \right).15 = 345{\rm{ }}\left( {c{m^2}} \right)\)
Thể tích của hình lăng trụ ABC.DEF là:
\(V = \left( {5.{\rm{ }}8} \right):2.15 = 300\left( {c{m^3}} \right)\)
a) Diện tích lưới cần mua chính là diện tích xung quanh của hình hộp chữ nhật.
S xq = C đáy .chiều cao.
b) Số tiền mua lưới = Diện tích lưới . 20 000.
a) Diện tích lưới cần mua là:
\({S_{xq}} = \left( {50{\rm{ }} + {\rm{ }}30} \right).2.8 = 1280\left( {{m^2}} \right)\)
b) Số tiền mua lưới là:
\(1280.{\rm{ }}20{\rm{ }}000 = 25{\rm{ }}600{\rm{ }}000\) (đồng)
Tính số tiền tăng ca mỗi ngày trong 3 giờ của anh Nam.
Tính số tiền tăng ca mà anh Nam nhận được trong tháng 11.
Làm tăng ca một ngày trong 3 giờ thì anh Nam nhận thêm được số tiền là:
\(320\,\,000:8.150\% .3 = 180\,\,000\) (đồng)
Số tiền tăng ca mà anh Nam nhận được trong tháng 11 là:
\(10\,\,300\,\,000 - 320\,\,000.26 = 1\,\,980\,\,000\) (đồng)
Anh Nam phải làm tăng ca ít nhất số ngày là:
\(1\,\,980\,\,000:180\,\,000 = 11\) (ngày).
Vậy anh Nam phải tăng ca ít nhất 11 ngày để có tổng tiền lương là \(10\,\,300\,\,000\) đồng .